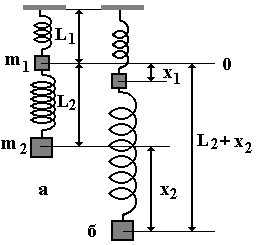
2.9. Понятие о связанных гармонических осцилляторах

Рассмотрим процесс малых колебаний двух пружинных маятников с массами грузов m₁ и m₂ и с коэффициентами жесткости пружин k₁ и k₂ соответственно, соединенных последовательно (рис.2.10).

Рис. 2.10

Силы сопротивления не учитываем. Данная система, выведенная из положения равновесия, будет совершать связанные гармонические колебания с двумя степенями свободы. Используя динамику поступательного движения, для связанных пружинных маятников, запишем уравнения движения грузов в следующем виде:

(2.43)

(2.44)

где

Используя метод характеристического уравнения, решения уравнений (2.43) и (2.44) запишем в виде: (2.45)

где А₁ и А₂  некоторые постоянные. В результате после подстановки уравнения (2.45) в (2.43) и (2.44), используя только вещественные части этих решений, окончательно получим:

x₁ = а₁ cos(₁t + ₀₁) + a₂ cos(₂t + ₀₂), (2.46)

x₂ = ₁а₁ cos(₁t + ₀₁) + ₂a₂ cos(₂t + ₀₂), (2.47)

где а₁, а₂, ₁, ₂ – некоторые постоянные;

причем (2.48)

Если ввести новые динамические переменные (обобщенные координаты) ₁ и ₂, т. е. ₁ = а₁cos (₁t + ₀₁), ₂ = а₂cos (₂t + ₀₂), то каждая переменная будет изменяться по гармоническому закону с амплитудами а₁ и а₂ и начальными фазами ₀₁ и ₀₂, соответственно. Совершаемые новыми динамическими переменными ₁ и ₂ простейшие гармонические колебания называют нормальными колебаниями системы связанных осцилляторов (нормальными модами).