5.5. Относительность длин

Длина стержня в ИСО равна разности координат его концов.

Например, , причем координаты х₁ и х₂ измеряются одновременно (наблюдатель покоится относительно стержня.

Однако результат изменяется, когда наблюдатель и стержень движутся друг относительно друга. В виду того, что понятие одновременности относительно и события

Рис. 5.3

одновременные в одной ИСО не будут одновременны в другой ИСО, поэтому длина стержня будет неодинаковой в различных ИСО.

Для вычисления длины стержня используют преобразования Лоренца.

Например, пусть некоторый стержень расположен параллельно оси 0Х в ИСО К, относительно которой он покоится.

Согласно рис. 6.3 длина стержня .

В ИСО К^*, движущейся относительно ИСО К равномерно и прямолинейно со скоростью v = const длина этого стержня

.

Используя преобразования Лоренца, имеем

т. е.

.

Если координаты концов отрезка в ИСО К^* одновременно

(так как ), то

(5.5)

Следовательно, длина отрезка в любой ИСО, относительно которой он движется, меньше длины отрезка в неподвижной ИСО.

Однако это не означает, что стержень деформируется в движущейся ИСО.

5.6. Интервал между двумя событиями

Любые события характеризуются точкой, где оно произошло, имеющей координаты х, у, z и временем t, т. е. каждое событие происходит в четырехмерном пространстве-времени с координатами х, у, z, t.

Если первое событие имеет координаты х₁, у₁, z₁, t₁, другое с координатами х₂, у₂, z₂, t₂, то величину

(5.6)

называют интервалом между событиями.

Если обозначить

и t₁₂ = t₂ – t₁,

то интервал

(5.7)

Найдем величину интервала между двумя событиями в любой ИСО.

Для этого будем считать, что в ИСО для системы К

S² = c²t² – x² - у² – z²,

где t = t₂ – t₁, x = x₂ – x₁, у = у₂ – у₁, z = z₂ – z₁.

Интервал между событиями в движущейся ИСО К^*

(S^*)² = c²(t^*)² – (x^*)² – (у^*)² – (z^*)².

Согласно преобразованиям Лоренца, имеем для ИСО К^*

; у^* = у; z^* = z; .

С учетом этого

(S^*)² = c²t² – x² – у² – z² = S² = inv. (5.8)

Следовательно, интервал между двумя событиями является инвариантом к переходу от одной ИСО к другой.

5.7. Релятивистский закон сложения скоростей

Используя преобразования Лоренца, имеем

Найдем скорость материальной точки (тела) в ИСО К

или (5.9)

Следовательно,

(5.10)

где u – скорость м. т. (тела) в ИСО К; u^* – скорость м. т. (тела) в К^*; v – относительная скорость движения ИСО К и К^*.

При u^* = c по формуле (5.9) для u имеем , т. е. тело не может двигаться со скоростью больше скорости света в вакууме.

5.8. Импульс в сто

Рассмотрим абсолютно упругий удар двух частиц с массами m₁ и m₂ в ИСО К и К^*.

Согласно закону сохранения импульса, для системы К

, (5.11)

где – соответственно перемещения и время движения частиц до удара;– соответственно перемещения и время движения частиц после удара.

Уравнение (5.11) запишем в проекциях на оси координат Х, У, Z:

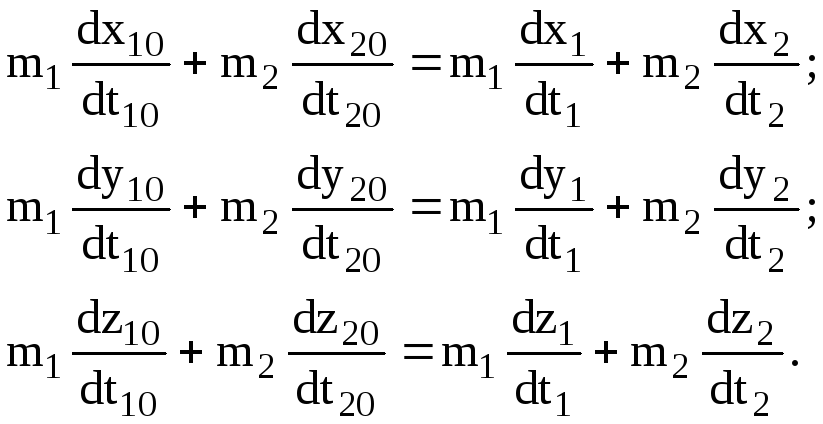(5.12)

Для рассмотрения этого явления в ИСО системы К^*, движущейся относительно системы К равномерно и прямолинейно со скоростью v = const, учтем, что

Отрезки же длин

dr₁₀; dr₂₀; dr₁; dr₂

сократятся в направлении оси 0Х в соответствии с формулой (6.5), но останутся неизменными в направлении осей У и Z, так как у^* = у, z^* = z.

В связи с этим

С учетом этого для ИСО К^* получим, что

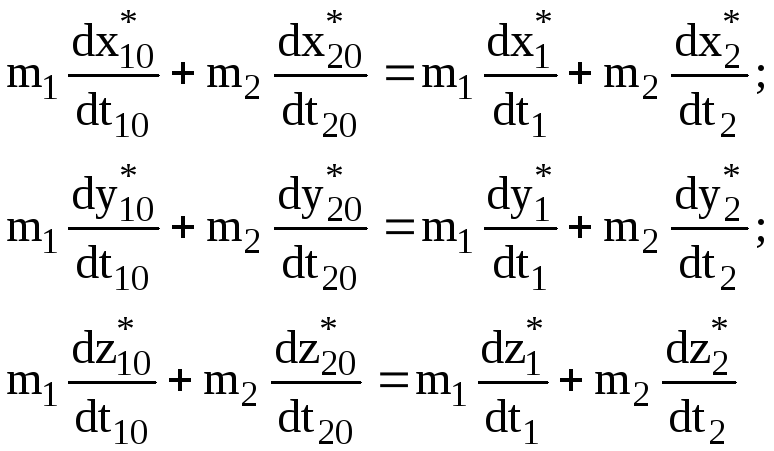(5.13)

или в векторном виде

. (5.14)

Анализ выражений (5.11) и (5.14) показывает, что представление импульса в виде

обеспечивает инвариантность закона сохранения импульса по отношению к преобразованиям Лоренца, где – перемещение частицы (м. т.) в той ИСО, в которой определяется импульс ее;dt – время, определяемое по часам, движущихся вместе с частицей (собственное время).

Так как,

то

, (5.15)

где

Следовательно, релятивистский импульс частицы

. (5.16)