1.16. Вычисление скорости равнопеременного

прямолинейного движения

Найдем скорость тела (м. т.) в любой момент времени.

По определению мгновенное ускорение

или .

При равнопеременном и прямолинейном движении м. т. вектор мгновенного ускорения с течением времени не изменяется ни по модулю, ни по направлению и совпадает с вектором среднего ускорения (a = const, ). Для того чтобы найти изменение скорости за конечный промежуток времениt, необходимо просуммировать изменение скорости по всем интервалам времени dt. Такое суммирование в математике выполняется операцией интегрирования, т. е.. После интегрирования.

Следовательно, скорость в любой момент времени

.

Если t₀ = 0, то (28)

При движении скорость тела линейно зависит от времени.

Векторное уравнение (28) соответствует системе трех скалярных уравнений для проекций на оси координат Х, У, Z:

Выражая проекции v_x, v_0x, a_x и т. д. через модули соответствующих векторов, нужно учитывать знаки («+» и «») и числовые коэффициенты, которые появляются в зависимости от направления проецируемого вектора и выбора положительного направления координатной оси. Например, при равнопеременном, и прямолинейном движении, происходящем вдоль оси Х, можно вместо векторного уравнения (28) написать соотношение v_x = v₀ + at, но только для случая, когда направления векторов совпадают с положительным направлением координатной оси.

Например, положительное направление координатной оси совпадает с направлением вектора начальной скорости , а положительный знак у слагаемого at соответствует ускоренному движению; положительный знак перед v_x говорит о том, что вектор конечной скорости направлен в ту же сторону, что и вектор начальной скорости.

Если при прочих равных условиях вектор противоположен по направлению вектору, то v_x = v₀  at. В зависимости от конкретных значений времени t, модулей начальной скорости v₀ и ускорения a результат расчета для v_x может привести как к положительному, так и к отрицательному значению. Рассмотрим конкретный пример.

Пусть м. т. совершает прямолинейное равнопеременное движение с начальной скоростью v₀ = 24 м/c и модулем ускорения а = = 4 м/с², но направления векторов противоположны, т. е.(а < 0).

Допустим, нас интересуют скорости м. т. через t₁ = 2 c и t₂ = 12 c после начала движения. Проецируя на координатную ось (например, ось Х), положительное направление которой совпадает с направлением вектора начальной скорости , и, выражая проекции векторов через их модули, получим, что через t₁ = 2 c скорость м. т. v_1x = 24  42 = 16 м/c.

При t₂ = 12 c v_2x = 24  412 = 24 м/c, т. е. проекция вектора скорости v_2x имеет знак минус. Это значит, что к моменту времени t₂ = 12 c после начала движения м. т. движется в противоположном направлении.

А когда же это произошло? В какой момент времени? Для этого в формуле v_x = v₀  at нужно скорость положить равной нулю, т. е. v_x = 0. Тогда v₀ = at или t = v₀ /a. После подстановки числовых значений имеем t = 6 с, т. е. через 6 с после начала движения м. т. изменила направление скорости на противоположное.

1.17. Путь равнопеременного, прямолинейного движения

Зная скорость в каждый момент времени v = v(t), можно найти путь, пройденный м. т. от момента времени t₁ до момента времени t₂.

Разделим промежуток времени t на N малых интервалов времени t_i (необязательно равных), где i = 1, 2 , 3, ... , N  номер интервала.

Согласно формуле мгновенной скорости v = dS / dt, можно считать, что путь S_i, пройденный м. т. за промежуток времени t_i, равен

S_i  v_i t_i,

где v_i  значение скорости м. т. за соответствующий промежуток времени t_i. Полный путь S, пройденный м. т., равен сумме отдельных отрезков пути S_i: S = S₁ + S₂ + ...+ S_N =или.

Если уменьшать интервалы времени t_i, то произведение v_i t_i будет с возрастающей точностью определять пройденный путь S_i. При t_i  0 в пределе получим истинное значение пути:

.

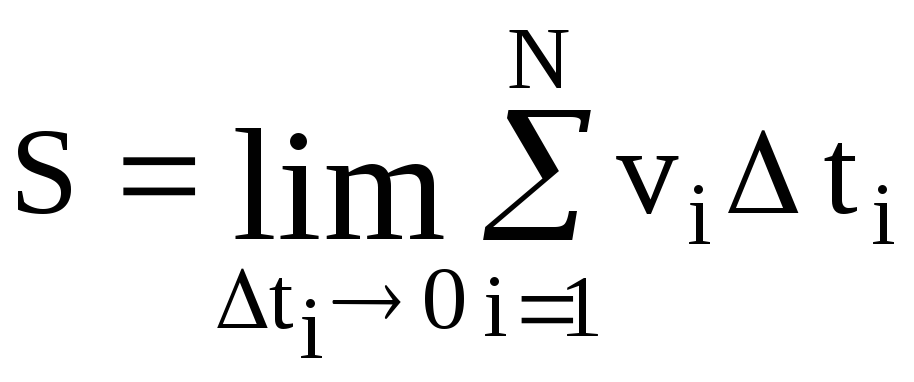В математике выражение данного вида называют определенным интегралом функции v = v(t), взятым по переменной времени t от t₁ (нижний предел) до t₂ (верхний предел), т. е.

Используя формулу скорости v = v₀ + at и формулу пути dS = v dt,

получим

.

После интегрирования найдем путь в виде

S = S₀+ v₀t + a t²/ 2. (29)

где S₀ – путь, пройденный м. т. к моменту времени t = 0.

Формулу вектора перемещения приведем без доказательства:

. (30)

Одному векторному уравнению можно сопоставить систему трех скалярных уравнений для определения изменения координат х, у, z за тот же промежуток времени при движении м. т., т. е.

х = х₀ + v_0xt + a_x t²/ 2,

y = y₀ + v_0yt + a_y t²/ 2, (31)

z = z₀ + v_0zt + a_z t²/ 2.

Из уравнения (1.31) можно получить уравнение, описывающее изменения радиус-вектора, характеризующего движение м. т. с течением времени в виде

. (32)

Примерами равноускоренного движения являются свободное падение тел в поле силы тяготения или скатывание тел по наклонной плоскости без учета сил трения и т. д.

Замечание: Существование начальных условий x₀, v₀, r₀ и т. д. вытекает из самой природы непрерывного течения времени и только в одном направлении от прошлого к будущему. Начальный момент времени t₀ = 0 не обязательно соответствует началу движения или выходу м. т. (частицы) из состояния покоя. Начальный момент времени можно выбирать произвольно. Это момент времени, с которого наблюдатель начал следить за данным движением или начал его исследовать. В этот момент обычно включается секундомер или иное устройство для измерения промежутков времени.