1.11. Мгновенная скорость

Уменьшая неограниченно промежуток времени t, за который произошло перемещение м. т. в пространстве в пределе, когда t  0, получим мгновенную скорость, т. е.

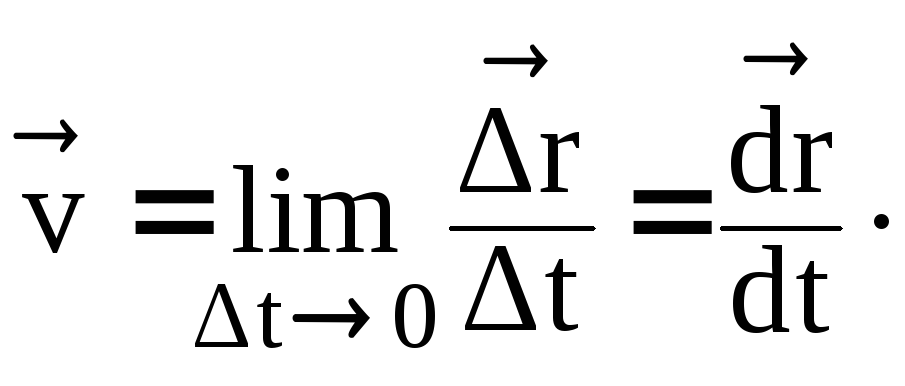(15)

Вектор мгновенной скорости равен пределу отношения приращения радиус-вектора м. т. к тому промежутку времени, за которое это приращение произошло, когда t  0 или равен первой производной радиус-вектора по времени.

Вектор мгновенной скорости в данный момент времени направлен по касательной к траектории в данной точке (рис. 9).

Действительно, при t  0, когда точка М₂ приближается к М₁, хорда (секущая) , сближается с длиной отрезка дугиs и в пределе s = , а секущая переходит в касательную. Это наглядно подтверждается опытами. Например, искры при заточке инструмента всегда направлены по касательной к точильному кругу. Поскольку, скорость – величина векторная, то модуль ее

.

В некоторых типах ускорителей (например, циклотронах и др.) частицы многократно движутся по замкнутой траектории без остановки. Следовательно, в любой точке траектории модуль вектора мгновенной скорости должен отличаться от нуля. Это заключение подтверждается не только уравнением (15), но и согласуется с понятием средней скалярной скорости (формула 11). Если в уравнении (11) перейти к пределу при t  0, то придется рассматривать такие малые участки пути на траектории s, которые не отличаются от модуля элементарного вектора перемещения . Тогда на основании уравнения (11) можно получить значение мгновенной скалярной скорости

совпадающее с модулем вектора мгновенной скорости ,

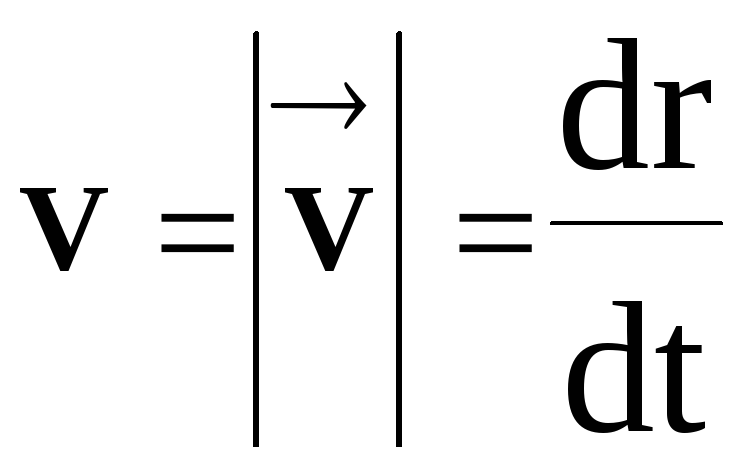так как r = s при t  0.

Одно уравнение вектора мгновенной скорости (15) можно заменить эквивалентной системой трех скалярных уравнений, проекций вектора скорости на оси координат

v_x = dx/dt, v_y = dy/dt, v_z = dz/dt. (16)

Вектор мгновенной скорости связан с его проекциями на оси координат выражением

, (17)

где – единичные векторы, направленные вдоль осей Х, У,Z соответственно.

По модулю

. (18)

Таким образом, вектор скорости характеризует быстроту изменения перемещения в пространстве по величине и направлению с течением времени. Скорость – функция времени.

1.12. Среднее ускорение

При движении тел скорость в общем случае может изменяться как по величине, так и по направлению.

Рис. 10

Примерами такого движения являются движение Солнечной системы вокруг центра нашей Галактики или движение поезда при торможении и т. д. Равномерное движение м. т. по окружности является примером, когда ее скорость изменяется по направлению, оставаясь постоянной по величине. Если м. т. движется по некоторой траектории, изменяя величину и направление скорости, то для характеристики ее движения уже недостаточно знать перемещение и скорость, нужно знать еще и быстроту изменения скорости, т. е. ускорение.

Пусть м. т. в некоторый момент времени t₁ находится в пункте М₁ и движется со скоростью , а в момент времени t₂ – в пункте М₂ – со скоростью (рис. 10).

Перенесем вектор параллельно самому себе в точку М₁ так, чтобы совпали начала векторов и.

Тогда разность векторов иесть вектор изменения (приращения) скорости за промежуток времениt = t₂ – t₁, т. е.

. (19)

Вектор среднего ускорения равен отношению вектора изменения скорости к промежутку времени, за которое это изменение произошло.

Следовательно,

. (20)

Вектор среднего ускорения совпадает с направлением вектора изменения скорости и, направлен внутрь кривизны траектории.

Одному векторному уравнению (1.20) соответствует система из трех скалярных уравнений для проекций вектора среднего ускорения на оси координат

(21)

Модуль вектора среднего ускорения

. (22)

За единицу измерения ускорения в СИ принят метр на секунду в квадрате.