1.9. Длина пути

При движении материальной точки по траектории используется кинематиче-ская характеристика – длина пути S (рис. 7).

Длина пути – скалярная величина, равна длине участка траектории, пройденного м. т. за рассматриваемый промежуток времени.

При прямолинейном движении м. т. в одном направлении =S, а в общем случае криволинейного движения , но различие между ними тем меньше, чем меньше , или при бесконечно малом промежутке времени dt, в случае произвольного криволинейного движения, равенство соблюдается при dr 0, т. е.

1.10. Средняя скорость материальной точки

Для количественного описания физических явлений используются различные физические величины, одной из них является скорость. Для оценки быстроты перемещения м. т. в пространстве с течением времени недостаточно знать траекторию и перемещение. Два же различных движения, для которых одно и то же перемещение совершилось за различные промежутки времени, геометрически одинаковы, но кинематически различны. Для характеристики быстроты изменения перемещения вводится понятие скорости.

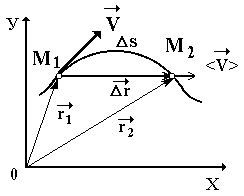
Пусть материальная точка движется и описывает некоторую траекторию в плоскости Х0У. В момент времени t₁ она находилась в точке М₁, характеризуемой радиус-вектором или координатами (х₁, у₁, z₁), в момент времени t₂ – в точке М₂, характеризуемой радиус-вектором или координатами (x₂, y₂, z₂). За промежуток времени t = t₂ – t₁ м. т. проходит по траектории путь s и получает элементарное перемещение, которое совпадает с приращением радиус-вектора за это время, т. е.

Вектором средней скорости называют физическую величину, равную отношению вектора перемещения (приращению радиус-вектора) к промежутку времени, за которое это перемещение произошло.

По определению вектор средней скорости . (9)

Вектор средней скорости направлен в ту же сторону, что и вектор перемещения (рис. 9).

В проекциях на оси координат вектора средней скорости с учетом (7) получаем три скалярных уравнения:

Рис. 9

Модуль средней скорости

. (10)

Замечание 1: Если м. т. движется по окружности или любой замкнутой траектории, т. е. через некоторое время возвращается в исходное положение, то ее перемещение равно нулю, следовательно, равна нулю и средняя скорость. Да, но тело-то двигалось! Для выхода из создавшегося положения вводят понятие средней скалярной скорости <v_c>, которая определяется отношением отрезка пути, пройденного м. т. по траектории за некоторый промежуток времени, к величине этого промежутка, т. е.

<v_c> = s / t. (11)

Если м. т. совершает ряд последовательных перемещений

,

за соответствующие промежутки времени t₁, t₂, ... , t_n, то вектор средней скорости результирующего перемещения находят по формуле

, (12)

а величину средней скалярной скорости – по формуле

. (13)

Замечание 2: Часто при решении задач для нахождения средней скорости используют формулу <v> = (v₀ + v_t) / 2 , (14)

где v₀ – начальная скорость, v_t – конечная.

Эта формула справедлива в случае прямолинейного равноускоренного или равнозамедленного движений и в одну сторону, т. е. без изменения направления скорости. Однако аналогичная формула в векторном виде

остается справедливой и в случае равнопеременного движения с изменением направления скорости.

В СИ за единицу измерения скорости принято м/c.