1.34. Векторная связь линейной и угловой скоростей

Пусть абсолютно твердое тело вращается вокруг неподвижной оси с угловой скоростьюВыберем на оси за начало отсчета т. 0 (рис. 21).

Рис. 21

Положение точки М характеризуется в данный момент времени радиус-вектором . Разложим радиус-векторна составляющие:Тогда, согласно рис.1.21, имеем. Эти векторы расположены во взаимно перпендикулярных плоскостях (рис. 22). Действительно, согласно (22) и рис. 21, имеем

v = R или v = r_, (64)

где R = r_, а угол между вектором угловой скорости и векторомравен 90^о. Согласно рис. 21 имеем r_= r sin . С учетом этого формула (64) примет вид v = r sin , т. е. имеем дело с векторным произведением

Рис. 1.22

. (65)

Так как

,

то формула (1.65) принимает вид

.

Учитывая, что векторное произведение двух коллинеарных векторов равно нулю (, рис. 21), получим

. (66)

Векторное произведение всегда связано с правилом правого винта.

Поэтому, вращая головку винта по направлению от вектора , стоящего на первом месте в (65), к вектору, стоящему на втором месте, определяем по поступательному движению винта направление третьего вектора, равного векторному произведению (рис. 22).

Вектор линейной скорости равен векторному произведению вектора угловой скорости и радиус-вектора.

Абсолютная величина этого векторного произведения

(67)

или v = r _  sin90^O= r _ , так как r sin  = r _.

1.35. Связь векторов тангенциального ускорения

и углового ускорения

Проведя аналогичные рассуждения, можно показать, что

. (68)

Вектор касательного ускорения равен векторному произведению вектора углового ускорения и радиус-вектора.

По модулю а_ =  r sin . Вектор нормального ускорения

, (). (69)

Рис. 23

Рис. 24

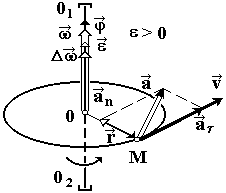
В заключение определим положение аксиальных векторов:

и полярных векторов: в случае равноускоренного > 0 (рис. 23) и равнозамедленного  < 0 (рис. 24) вращения м. т. вокруг неподвижной оси.