1.26. Среднее угловое ускорение

Из анализа равенства (47) следует, что угловая скорость  может изменяться как за счет изменения линейной скорости v при вращении (в этом случае угловая скорость изменяется по величине), так и за счет поворота оси вращения в пространстве. При неравномерном вращении тела вокруг неподвижной оси угловая скорость изменяется только по величине, оставаясь постоянной по направлению.

Если при вращении (R = сonst) за некоторое время t угловая скорость получит приращение , то линейная скорость получит приращение v, т. е.

v = R . (51)

Разделим правую и левую части равенствa (51) на время t, за которое произошло вращение, получим, что

.

Отношение (52)

– называют средним угловым ускорением.

Средним угловым ускорением тела называют отношение изменения угловой скорости к промежутку времени, в течение которого это изменение произошло.

1.27. Мгновенное угловое ускорение

При t  0 в пределе получим абсолютное значение мгновенного углового ускорения:

(53)

т. е. мгновенное угловое ускорение численно равно первой производной угловой скорости по времени или – второй производной углового перемещения по времени.

1.28. Связь линейного и углового ускорений

Используя равенство (1.52) и переходя к пределу, получаем

.

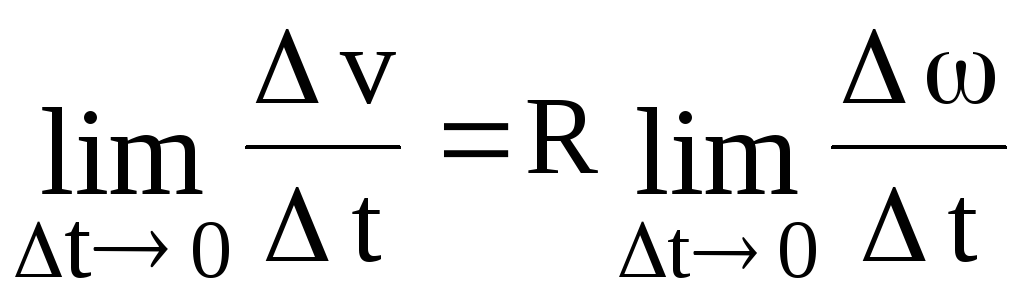Учитывая, что , так как тангенциальное ускорение, характеризует изменение скорости только по величине имеем

а_ = R  . (54)

В СИ единицей измерения углового ускорения является радиан на секунду в квадрате (рад/c² или с^-2).

1.29. Связь линейных величин s, V, a c угловыми , , 

Полученные равенства

s = R , v = R , a_ = R  (55)

показывают, что линейные кинематические величины s, v, a_, характеризующие движение отдельных точек тела, получаются умножением кинематических угловых величин , , , отражающих движение всего тела в целом на расстояние от этих точек до оси вращения (радиусы). При вращательном движении абсолютно твердого тела линейные скорости точек тела направлены по касательным к траекториям (окружности) и непрерывно изменяют направление. При равномерном вращении тела быстрота изменения направления скорости характеризуется нормальным ускорением

а_n ==² R. (56)

Вследствие того, что для всех точек тела  = const, а_n по абсолютной величине растет при удалении от оси вращения. Используя связь полного, нормального и касательного ускорений и учитывая (1.54) и (1.56) имеем

. (57)