4.9. Энергия волн
При распространении волн в среде происходит перенос энергии волной. В это время в среде наблюдаются колебания ее частиц, т. е. частицы среды приобретают кинетическую (за счет движения) и потенциальную (за счет деформаций) энергии.
Найдем объемную плотность кинетической энергии wk cреды, в которой распространяется волна:
,
(4.19)
где плотность среды;
v скорость колебания частиц cреды.
Скорость постоянна (v = сonst) в пределах объема dV.
Запишем формулу объемной плотности потенциальной энергии cреды:
,
(4.20)
где плотность среды; vф фазовая скорость волны в среде; относительная деформация.
Полная объемная плотность механической энергии волн в среде равна сумме объемных плотностей кинетической и потенциальной энергий, т. е.
.
(4.21)
При распространении волн в среде непрерывно происходит передача энергии все новым и новым участкам среды за счет энергии источника.
В связи с этим объемная плотность полной механической энергии волн зависит и от координат, и от времени.
Объемная плотность полной энергии волн (см. гл. 6) за период
(4.22)
4.10. Поток энергии. Вектор Умова
Если на пути распространения волны поставить некоторую площадку dS, то в этом случае говорят о потоке энергии через эту площадку.
Отношение энергии, переносимой сквозь некоторую площадку к промежутку времени, за который произошел ее перенос, называют потоком энергии.
Согласно определению можно записать формулу потока энергии:
dФэ=
.
(4.23)
Используя объемную плотность энергии w, запишем полную энергию волны
dW= w (vdt) dS сos ,
где
=
vdt
расстояние, на которое перемещается
волна, имея скорость v за малое время
dt;
угол между векторами скорости и нормалью
к площадке (рис. 4.6) или
Рис. 4.6
,
где
.
Следовательно, поток энергии переносимый волной
(4.24)
или
(4.25)
где
(4.26)
называют вектором Умова, или вектором плотности потока энергии.
Вывод:
Модуль
вектора Умова характеризует плотность
потока энергии волны, переносимой через
площадку перпендикулярно направлению
распространению волны,
т. е., U =
.
Мощность потока энергии волны характеризуют интенсивностью волны.
Модуль среднего значения вектора плотности потока энергии волн, называют интенсивностью J .
Интенсивность волны энергия, переносимая волной через единицу поверхности за единицу времени перпендикулярно к направлению распространению волны.
Для плоской бегущей и сферической синусоидальных волн за период интенсивность волны определяется выражением
.
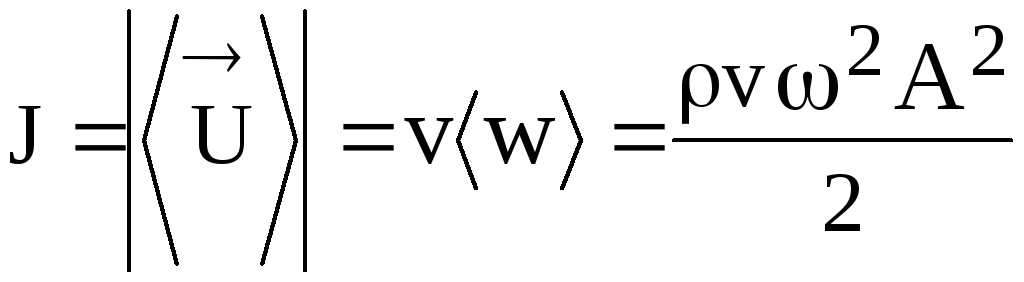(4.27)
Реальные среды, в которых распространяются волны, всегда поглощают энергию. При этом происходит уменьшение амплитуды и интенсивности волны, т. е. волны затухают.