18

Физика колебаний и волн

Лекция 11

4.4. Уравнение плоской бегущей волны

Для описания волновых процессов используют волновые уравнения. Например, уравнение плоской бегущей волны можно представить в общем виде s(х, y, z, t) = 0. (4.3)

В общем случае волны распространяются в пространстве в какой-то среде. При описании волн будем считать, что они распространяются, например, вдоль оси Х, т. е. только вдоль одного направления. Если источник колебаний будет находиться в начальный момент времени в точке 0, то спустя некоторое время  после возбуждения колебаний, волна, распространяясь со скоростью v в направлении оси Х, достигнет точки М с некоторым запаздыванием (рис. 4.3), т. е.

t = t   = t  х / v,

где х  расстояние от источника колебаний до точки М;

v  скорость распространения волны.

Рис. 4.3

Таким образом, от уравнения колебаний

s = Аcos(t + _o)

переходим к уравнению бегущей плоской волны

(4.4)

или

(4.5)

Используя формулу длины волны (4.1), перепишем последнее уравнение в виде

или

, (4.6)

где k ==(4.7)

 волновое число.

В связи с тем, что волны распространяются в средах с пространственными координатами x, y, z и в течение некоторого времени t, используют понятие волнового вектора .

Положение частиц среды, до которых распространилась волна, определяют радиус-вектором .

Поэтому уравнение волны можно представить в следующем виде:

, (4.8)

где

.

Без вывода приведем уравнение сферической волны, когда среда не поглощает энергию:

(4.9)

где  амплитуда сферической волны.

4.5. Волновое уравнение

Для однородной, изотропной, непрерывной среды, которая не поглощает энергию вместо уравнения волны используют волновое уравнение, представляющее собой дифференциальное уравнение в частных производных.

Волновое уравнение можно получить, если найти вторые частные производные по каждой из координат, используя уравнение плоской бегущей волны (4.8)

,

, (4.10^*)

,

.

После сложения производных по координатам, используем оператор Лапласа,

или

Запишем волновое уравнение:

или (4.10)

Если волна при распространении изменяется по гармоническому закону, то она одновременно удовлетворяет двум дифференциальным уравнениям:

1) s =  k²s, 2) . (4.11)

4.6. Фазовая скорость

Скорость распространения волны входит в значение фазы волны (4.5).

Фазовой называют скорость, с которой распространяется синусоидальная волна в данной среде.

Эта скорость равна скорости перемещения точек поверхности в пространстве, если значение фазы постоянно.

Действительно, для плоской бегущей волны, имеем

t  kx + _o = const.

После дифференцирования, получим

 k(dx/dt) = 0

или

v_ф = dx/dt =  / k . (4.12)

Например,

1. Фазовая скорость распространения звука в газах или жидкостях

v_ф² =,

где К  объемная упругость среды;   плотность среды.

2. Если газ идеальный, то v_ф²=,

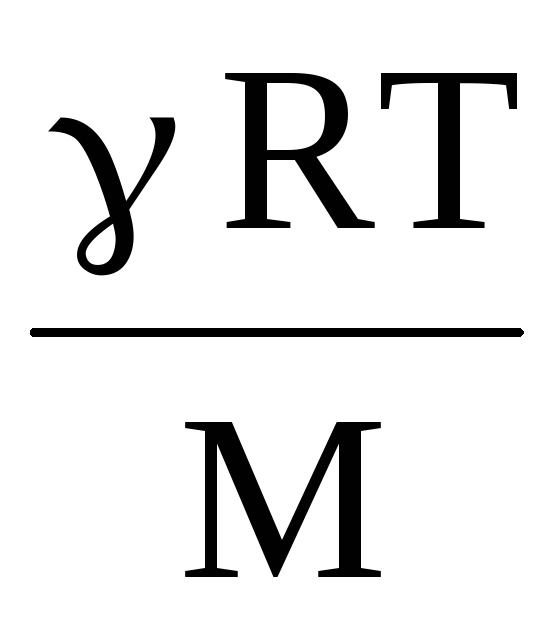где   показатель адиабаты; R  газовая постоянная; Т  абсолютная температура; М  молярная масса газа.

3. В однородной изотропной среде (твердое тело) фазовая скорость поперечных синусоидальных волн

v_ф² = ,

где G  модуль сдвига твердой среды;   плотность среды.

4. Фазовая скорость распространения поперечных волн вдоль струны

v_ф² = ,

где F_нат  сила натяжения струны;   плотность материала струны; S  площадь сечения струны.