1.2. Взаимодействие электрических зарядов. Закон Кулона.

В 1785 г. Кулон экспериментально установил зависимость силы взаимодействия зарядов от их величины, знака и расстояния между ними.

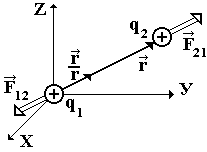
Сила взаимодействия двух точечных зарядов, находящихся в вакууме, прямо пропорциональна произведению зарядов и обратно пропорциональна квадрату расстояния между ними, направлена вдоль прямой линии, соединяющей эти заряды (рис. 1.1)..

Рис. 1.1

В СИ закон Кулона запишем в виде

, (1.2)

где _о = 8,8510^12  электрическая постоянная;  единичный вектор.

При решении задач удобно использовать величину

= 910⁹ .

Согласно третьего закона Ньютона

F₁₂ =F­₂₁= F.

Знак силы взаимодействия зарядов зависит от знака этих зарядов. Притяжению соответствует знак «  », разноименные заряды притягиваются, отталкиванию  « + », одноименные заряды отталкиваются (рис. 1.2, а, б).

По абсолютной величине закон Кулона

. (1.3)

а б

Рис. 1.2

Если заряды находятся в диэлектрической среде, то

, (1.4)

где   диэлектрическая проницаемость среды,

. (1.5)

В СИ заряд измеряют в кулонах (Кл).

На основании экспериментальных данных установлено, что закон Кулона справедлив для расстояний от 10^15 м до нескольких километров, а возможно и до бесконечности.

1.3. Электрическое поле

Взаимодействие между зарядами (согласно современным представлениям) осуществляется посредством электрического поля. Если заряды неподвижны, то поле называют электростатическим.

Любой электрический заряд q создает в окружающем его пространстве электрическое поле (изменяет свойства этого пространства). Электрическое поле проявляет себя в том, что помещенный в любую точку этого поля «пробный» заряд испытывает действие кулоновской силы со стороны этого поля. Основной количественной характеристикой электрического поля является вектор напряженности .

Напряженность электростатического поля  сила, действующая на единичный, положительный точечный неподвижный пробный заряд.

Замечание: пробный заряд q_o должен быть достаточно малым, чтобы его внесение в электрическое поле не вызывало заметного искажения его.

На основании опытов установлено, что напряженность электрического поля и кулоновская сила, действующая на внесенный в это поле пробный заряд, связаны соотношением

, (1.6)

где  вектор напряженности электростатического поля в данной точке.

Напряженность поля неподвижного точечного заряда q в вакууме на расстоянии r от него

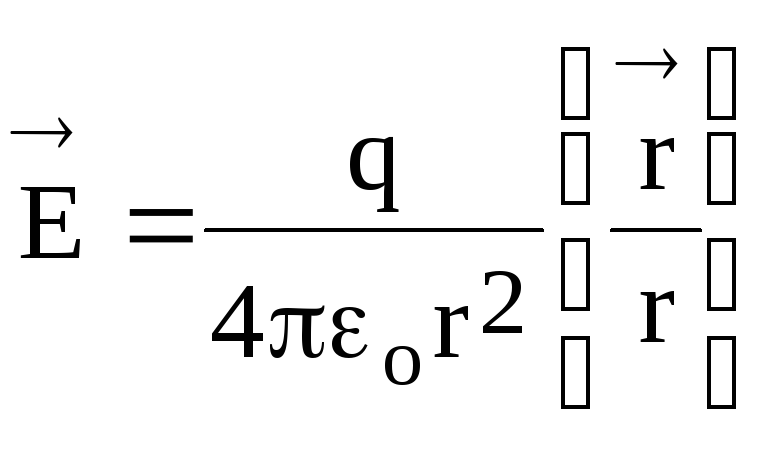(1.7)

или по модулю

, (1.8)

Рис. 1.3

где r  расстояние от заряда q, создающего электрическое поле, до точки пространства, в которой определяется напряженность этого поля (рис. 1.3).

Если заряд находится в безграничной среде с диэлектрической проницаемостью , то

. (1.9)

В электрическом поле, создаваемом неподвижным точечным зарядом, сила, действующая на внесенный пробный заряд, не зависит от того, покоится пробный заряд или движется. Это относится и к системе неподвижных зарядов.

Напряженность в СИ измеряется в вольтах на метр (В/м).

Если мы имеем систему точечных неподвижных зарядов, то можно определить напряженность результирующего электрического поля в произвольной точке этого поля (принцип суперпозиции).

Вектор напряженности поля системы точечных неподвижных зарядов равен векторной сумме напряженности полей, созданной каждым из зарядов в отдельности, т. е.

(1.10)

или , (1.11)

где _i  вектор напряженность поля, созданного i м точечным зарядом на расстоянии r_i от него.