8. Емкостные коэффициенты

Решения задачи о нахождении электрических полей в системе N статических заряженных проводников упрощаются, если воспользоваться следующим свойством: заряды проводников являются линейными, однородными функциями их потенциалов, а потенциалы  линейными, однородными функциями зарядов.

Коэффициенты этих линейных зависимостей называют емкостными коэффициентами, которые определяются размерами, формой и взаимным расположением проводников. Если пространство между проводниками заполнено однородным диэлектриком, в котором нет свободных зарядов, то емкостные коэффициенты прямо пропорциональны его диэлектрической проницаемости. Согласно линейности и однородности уравнений электростатики (например, уравнение Лапласа) аналитически это свойство записывается в виде

, (14)

где q_i  заряд i-го проводника; _j  потенциал j-го проводника; С_ij  емкостные коэффициенты ( индексы i, j = 1, 2, ... , N).

В свою очередь, емкостные коэффициенты характеризуются следующими свойствами: 1) С_ij = С_ji; 2) С_ii  0 для всех i. Действительно, емкостные коэффициенты С_ij с одинаковыми индексами (I = j) положительны. Заземлим все проводники, кроме i -го и j - го, тогда q_i = C_ii_i. Но величины q_i и _i имеют одинаковые знаки.

Следовательно, С_ii  0. 3) С_ij  0, если I  j, т. е. емкостные коэффициенты с различными индексами  отрицательны. Действительно, заземлим все проводники, кроме i -го и j- го. Сообщим i -му проводнику положительный заряд (q_i 0), а j-й  останется не заряженным (q_j=0),а потенциалы _i и _j будут положительными. Причем q_j = С_ji_I + C_jj_j = 0, что возможно, если С_ji  0. Во всех случаях потенциал поля в бесконечности равен нулю. Если число проводников (обкладок конденсатора) равно двум, то

q₁ = C₁₁ ₁ + C₁₂ ₂,

q₂ = C₂₁ ₁ + C₂₂ ₂, (15)

где +q=q= q.

Решая уравнения (14) относительно ₁ и ₂, находим разность потенциалов и емкость конденсатора: . (16)

9. Соединение конденсаторов в батарею

Для изменения емкости конденсаторов их соединяют в батарею. Различают последовательное, параллельное и смешанное соединения.

9.1. Последовательное соединение конденсаторов

Рис. 12

Все внутренние обкладки при последовательном соединении электризуются через влияние. Их заряды равны

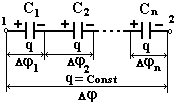
по величине, но противоположны по знаку (+q=q = q; рис. 12).

Следовательно, заряды на всех конденсаторах при последовательном их соединении равны, а потенциалы складываются,

т. е.

 = ₁ ₂ = ₁ + ₂ + ... + _n,

Но ,

где .

Следовательно, . (17)