6. Электрическая емкость проводников

Рассмотрим проводник, изолированный от влияния других проводников и заряженных тел. При сообщении заряда q проводнику возникает потенциал, пропорциональный этому заряду (  q). Опыт показывает, что отношение заряда проводника к его потенциалу уже не зависит ни от заряда, ни от потенциала, является для данного проводника величиной постоянной, которую называют электрической емкостью проводника С (емкостью), т. е.

С = q /  (4)

Найдем емкость проводящего шара радиуса R.

Потенциал на поверхности заряженного шара можно найти т. е. , где напряженность поля заряженной сферы (при r = R); _ = 0.

После интегрирования получим

(5)

или при наличии диэлектрика , (6)

когда окружающая шар диэлектрическая среда характеризуется диэлектрической проницаемостью . После подстановки вместо потенциала его значение [формула (6)] в (5) имеем

С = 4_оR. (7)

Следовательно, емкость проводника зависит только от размеров и формы, диэлектрической проницаемости окружающей среды и наличия вблизи других проводников. В СИ емкость измеряют в фарад: (1 мкФ = 10^6 Ф;

1 пФ = 10^12 Ф). Например, электроемкость Земного шара,  С  0,7 мкФ.

7. Конденсаторы

Рис. 9

Если вблизи заряженного проводника находятся другие проводники, то емкость его будет увеличиваться, так как электрическое поле вызывает появление на других проводниках индуцированных зарядов. Например, если заряд проводника положительный, то отрицательные индуцированные заряды на других телах располагаются ближе к проводнику, что приведет к уменьшению потенциала данного проводника, а емкость увеличится. Систему двух разноименно заряженных плоскостей (обкладок) называют плоским конденсатором (рис.9).

Их заряды равны по абсолютной величине (+q=q= q).

Если расстояние между обкладками много меньше их размеров, то электрическое поле является практически однородным и сосредоточено между обкладками. Вне конденсатора поле практически равно нулю.

Основной характеристикой конденсатора является электрическая емкость , (8)

где   разность потенциалов между его обкладками.

Напряженность электрического поля между его обкладками

, (9)

где q = S; где   поверхностная плотность заряда на обкладках конденсатора; S  площадь его обкладок.

Используя связь напряженности с разностью потенциалов, в виде  = Еd. После подстановки q, E и  получим

. (10)

Если пространство между обкладками конденсатора заполнено диэлектриком с проницаемостью , то . (11)

Рис. 10

Анализ формулы (11) показывает, что емкость плоского конденсатора зависит только от размеров обкладок, расстояния между ними и диэлектрической проницаемости  вещества между обкладками. Кроме плоского конденсатора, на практике используют сферический и цилиндрический конденсаторы. Найдем емкость сферического конденсатора, который представляет собой систему двух концентрических сфер с общим центром. Пусть радиусы внешней и внутренней сфер (обкладок) соответственно равны R₂ и R₁ (рис. 10). Если внутренняя обкладка конденсатора заряжена положительно, а внешняя  отрицательно, то электрическое поле создается вне сферы. Поэтому результирующее поле вне конденсатора равно нулю. В пространстве между обкладками поле создается только зарядом внутренней обкладки.

Применяя теорему Гаусса, найдем напряженность поля между сферическими обкладками конденсатора по формуле

, где q  заряд конденсатора.

Используя последнее выражение где = dr, найдем разность потенциалов между обкладками сферического конденсатора:

.

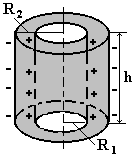
Рис. 11

Cледовательно, емкость сферического конденсатора, с учетом того, что пространство между обкладками заполнено диэлектрической средой с проницаемостью : . (12)

Найдем емкость цилиндрического конденсатора, представляющего собой систему двух цилиндров, вставленных один в другой с общей осью.

Проводя аналогичные рассуждения, как и в случае со сферическим конденсатором, получим

, (13)

где h  высота образующей цилиндрического конденсатора;   диэлектрическая проницаемость среды, заполняющей пространство между обкладками цилиндрического конденсатора; _о  электрическая постоянная; R₂ и R₁  радиусы основания внешней и внутренней его цилиндрических обкладок (рис. 11).