Конспект лекций по физике 2 части / Лекция 13 маг 2007

8

Электричество и магнетизм Н.Ф. Шемяков

Лекция 13

6.14. Закон Био-Савара-Лапласа

Рис. 6.21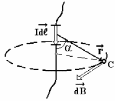

При своем движении электрические заряды в проводах создает в окружающем пространстве магнитное поле. Магнитное поле создает не только ток проводимости, но и любой ток: ток в газах, ток смещения. Найдем индукцию магнитного поля, созданного элементом проводника с током (рис. 6.21). Для этого воспользуемся формулой магнитной индукции равномерно движущегося заряда. Введем объемную плотность заряда,

т. е. q = dV, где dV - элемент объема, тогда

. (6.64)

Плотность тока в элементе проводника j = n_oqv = (N=1).

Поэтому формулу (6.64) перепишем в виде

. (6.65)

Если ток течет по проводу площадью поперечного сечения S,

то объемный элемент тока jdV равен линейному элементу тока , т. е.

jdV = .

С учетом этого формула (6.65) принимает вид (6.66)

или . (6.67)

Формулы (6.66) и (6.67) называют законом Био-Савара-Лапласа.

В общем случае расчет индукции магнитного поля тока, текущего в проводах произвольной формы, по формуле (6.66) довольно сложен. Если же распределение тока имеет некоторую симметрию, например, магнитное поле прямого и кругового токов, то расчет индукции магнитного поля значительно упрощается, если воспользоваться принципом суперпозиции магнитных полей, т. е. .

6.15. Магнитное поле прямого проводника с током

Найдем индукцию магнитного поля dB произвольного элемента прямого проводника c током конечной длины АС (рис. 6.22).

По закону Био - Савара - Лапласа индукцию магнитного поля, созданную элементом проводника с током в произвольной точке К, можно найти по формуле

. (6.68)

В этой формуле три переменные величины: элементом длины проводника , r - расстояние до этого элемента,  - угол, под которым виден из данной точки К элементом длины проводника.

Поэтому приведем формулу к одной переменной , введя известные величины: d - кратчайшее расстояние от точки К до проводника с током; I - сила тока в проводнике; и углы: ₁, ₂.

Согласно рис. 6.22 имеем .

Рис. 6.22

С учетом этого формула (3.23) принимает вид

. (6.69)

Используя принцип суперпозиции, находим результирующую индукцию магнитного поля прямого проводника с током длины АС в точке К,

т. е. .

После интегрирования имеем

. (6.70)

или .

Если проводник бесконечной длины, то ₁ = 0^о, ₂ =180^о.

Следовательно, индукция магнитного поля прямого проводника бесконечной длины в произвольной точке К окружающего пространства

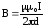. (6.71)

или .

6.16. Магнитное поле кругового тока

Найдем индукцию магнитного поля кругового тока на оси витка в произвольной точке А (рис. 6.23). Согласно закону Био - Савара - Лапласа индукцию магнитного поля, созданную элементом проводника с током _i в произвольной точке А на оси Х, можно найти по формуле

, где sin = 1. (6.72)

Из-за симметрии от элементов витка с током в точке А будет образован конус векторов . Направление вектора индукции можно определить по правилу правого винта: если головку винта вращать по направлению

тока в витке, то поступательное движение винта укажет направление вектора индукции.

Рис. 6.23

Проекция вектора индукции магнитного поля, созданного элементом проводника с током _i на ось Х,

,

где dB₁ = dB₂ =...= dB_n = dB_i.

Результирующая индукция магнитного поля в точке А витка с током

, (6.73)

где R - радиус витка. Согласно рис. 6.23 имеем cos  = , r² = R² + h², где h - расстояние от центра витка до точки А. После подстановки в (6.73) и интегрирования получим

. (6.74)

или

При h = 0 индукция в центре витка

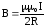. (6.75)

или

6.17. Момент сил, действующий на контур с током

Если контур с током (I = const) поместить в неоднородное внешнее магнитное поле, то на него будет действовать сила Ампера, т. е.

. (6.76)

В однородном магнитном поле результирующая сила Ампера, действующая на контур с током, равна нулю:

. (6.77)

Рассмотрим плоский контур с током малых размеров (магнитный листок), который называют элементарным. Такой контур характеризуют вектором магнитного момента

, (6.78)

Рис. 6.24

где I  сила тока в витке; S  площадь витка ограниченного контуром L;  вектор нормали, направление которого связано с направлением тока в витке правилом правого винта (рис. 6.24).

По модулю

р_m = IS. (6.79)

В СИ магнитный момент измеряется в амперах на метр в квадрате (Ам²).

Если контур не плоский, то

, (6.80)

где интеграл зависит только от выбора контура L, на который натянута поверхность S. Расчеты показывают, что эту силу можно записать в виде

, (6.81)

где р_m  модуль магнитного момента контура;  частная производная вектора по направлению вектора нормали (по направлению ).

Проекция силы, например, на направление оси Х

. (6.82)

В однородном магнитном поле F = 0, так как = 0.

Результирующий момент сил Ампера, действующий на контур, запишем в виде

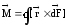(6.83)

или в виде

, где (рис. 6.25). (6.84)

Рис. 6.25

Пара сил Ампера действует на стороны b контура; на стороны а контура действуют силы, стремящиеся только растянуть его, на рис. 6.25 они не показаны. По модулю вращающий момент сил Ампера

М = р_mВsin = ISBsin, (6.85)

где   угол между векторами и .

При  = 0^о, М = 0 ( ) положение контураустойчиво. При  = 180^о, М = 0 ( ) положение контура  неустойчиво.

Если магнитное поле неоднородно и размеры контура малы, то влиянием неоднородности можно пренебречь.

6.18. Работа перемещения контура с током

в магнитном поле

Рис. 6.26

На любой проводник с током в магнитном поле действует сила Ампера.

В однородном магнитном поле работа, совершаемая силой Ампера (рис. 6.26),

А = Fx,

где

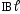
F =  сила Ампера

т. е. А = IB()x

или

А = IBS,

где S =()x

или А = IФ_м,

где Ф_м =BS.

В неоднородном магнитном поле элементарная работа dA, совершаемая силой Ампера при бесконечно малом перемещении элемента проводника с током ,

(6.86)

где

;

 вектор малой площадки, возникающей при перемещении элемента проводника с током на малое перемещение ;  магнитный поток, пронизывающий эту площадку (рис. 6.27).

Рис. 6.27

Следовательно, при перемещении проводника конечной длины , по которому течет ток, в переменном магнитном поле, из состояния 1 в 2 совершается работа

. (6.87)