21

Электричество и магнетизм Н. Ф. Шемяков

Лекция 15

6.2. Магнитное поле в веществе

6.2.1. Магнитный момент атома

Все вещества состоят из молекул и атомов.

Атом состоит из ядра, содержащего положительно заряженные протоны и нейтроны, не имеющие заряда. Вокруг ядра обращаются отрицательно заряженные электроны. При движении электрона вокруг ядра по орбите радиуса r со скоростью v возникает микроток

I = q_e = , (4.41)

где   частота обращения электрона по орбите; q_e  заряд электрона.

Движение электрона по орбите характеризуют:

1) орбитальным магнитным моментом (рис. 6.11), модуль которого

р_m = IS = , где S =r²  площадь орбиты; (4.42)

Рис. 4.11

2) орбитальным моментом импульса , модуль которого L_e = mvr, (4.43)

где m  масса электрона.

Вектор противоположен по направлению вектору.

Отношение (4.44)

называют гиромагнитным отношением.

Кроме орбитального, электрон обладает собственным (спиновым) моментом импульса  , с которым связан собственный магнитный момент, и характеризуется спиновым гиромагнитным отношением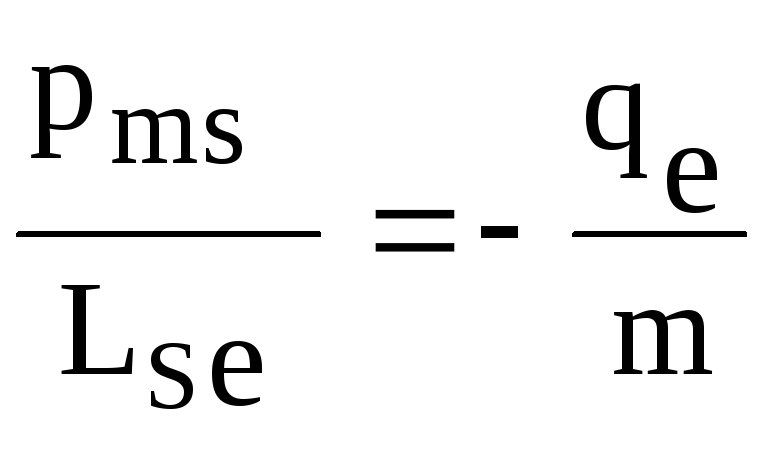. (4.45)

Элементарным магнитным моментом электрона является магнетон Бора

. (4.46)

Чтобы найти полный магнитный момент атома, надо сложить магнитные моменты всех электронов, входящих в состав атома и магнитный момент ядра. Магнитный момент ядра в ≈1840 раз меньше магнитного момента электрона и в дальнейшем его рассматривать не будем.

6.2.2. Атом в магнитном поле

При движении электрона вокруг ядра по орбите радиуса r на него действует центростремительная сила

.

Если атом внести во внешнее магнитное поле, вектор индукции которого перпендикулярен плоскости орбиты электрона, то на электрон начнет действовать силаЛоренца

,

где   круговая частота обращения электрона в магнитном поле.

Уравнение движения электрона в магнитном поле запишем в виде

m²r = F_цс  F_л

или

m²r = ,

где знаки «» выбираются в соответствии с относительной ориентацией векторов и.

После преобразования последнего выражения получим

mr(  _o) ( + _o) = 2mr =  q_erB,

где  =-_o << ; 2  +_o.

Из последнего выражения найдем, что

_L =  = 

или в векторном виде

. (4.47)

Таким образом, в магнитном поле электрон получает дополнительную угловую скорость вращения, которую называют частотой Лармора.

Причем векторы _L и cовпадают по направлению (рис.4.12).

Рис. 4.12

Частоту Лармора приобретают все электроны атома, так как она не зависит от радиуса орбиты и скорости движения электрона.

Скорость электрона при внесении атома в магнитное поле изменяется, поэтому изменяется и его кинетическая энергия W_k.

Но так как радиус вращения остается неизменным, то потенциальная энергия электрона не изменяется.

За счет чего же изменяется энергия электрона в атоме, если магнитное поле действует перпендикулярно скорости и не производит работы?

Частота Лармора возникает в момент включения магнитного поля.

Следовательно, переменное магнитное поле возбуждает переменное электрическое поле, которое и сообщает электрону дополнительное вращение с частотой Лармора.

Таким образом, возникновение ларморовского вращения вызвано проявлением электромагнитной индукции.

Это явление наблюдается во всех без исключения веществах при внесении их в магнитное поле. Векторы иначинают прецессировать вокруг направленияс частотой Лармора (векторописывает коническую поверхность, рис. 4.12.).

Теорема Лармора: Единственным результатом влияния магнитного поля на орбиту электрона в атоме является прецессия орбиты и вектора с угловой скоростью_L вокруг оси, проходящей через ядро атома и параллельно вектору индукции внешнего магнитного поля.

Рис. 4.13

В результате прецессии наводится дополнительный орбитальный магнитный момент электрона, модуль которого

р_m = IS_ =, (4.48)

где I = q_e, _L = 2; S_  площадь проекции орбиты электрона на плоскость, перпендикулярную (рис. 4.13).

Так как вектор противоположен по направлению вектору , то

= . (4.49)

Если атом содержит Z электронов, то наведенный магнитный момент

= , (4.50)

где < S_ >  cреднее значение площади S_ для орбит всех электронов атома.

При суммировании орбитальных и спиновых магнитных моментов атомов может произойти их полная компенсация.

Тогда результирующий магнитный момент атома равен нулю.

Если такой компенсации не происходит, то атом имеет постоянный магнитный момент. Вещества, у которых атомы в отсутствие внешнего магнитного поля имеют постоянный магнитный момент, не равный нулю, могут быть парамагнетиками, ферромагнетиками, антиферромагнетиками или ферримагнетиками.