6.7. Применение теоремы о циркуляции

6.7.1. Магнитное поле соленоида

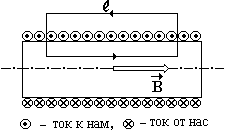
Соленоидом называют катушку с током, витки которой намотаны вплотную друг к другу на цилиндрический каркас (рис. 6.9). Если длина соленоида много больше его диаметра, то магнитное поле снаружи его практически равно нулю. Магнитное поле внутри соленоида можно считать однородным.

Силовые линии магнитного поля направлены вдоль оси, причем вектор составляет с направлением тока в соленоиде правовинтовую систему.

Рис. 6.9

Найдем индукцию магнитного поля соленоида в центре на его оси, используя теорему о циркуляции .

Пусть прямоугольный контур охватывает n витков (n  число витков на единицу длины соленоида, т. е. n , где N  полное число витков соленоида;  длина соленоида, витки с током которого охвачены прямоугольным контуром).

Циркуляция векторапо данному контуру.

Контур охватывает суммарный ток .

Согласно теореме о циркуляции , имеем В=₀nI.

Следовательно, индукция магнитного поля внутри соленоида

В = ₀nI, (6.33)

где nI  число ампервитков.

6.8. Проводник с током в магнитном поле

Сила , действующая на элемент длины проводника с током в неоднородном магнитном поле (рис. 6.10) ,

Рис. 6.10

(6.34)

или

dF = IdВsin. (6.35)

Формулы (6.34), (6.35) называют законом Ампера.

Интегрируя эти выражения по элементам тока, находим силу Ампера, действующую на линейный или объемный участок проводника с током (при условии, что ток течет по тонкому проводнику,

Рис. 6.11

jdV = Id),

т. е. . (6.36)

Направление силы Ампера можно найти по правилу правого винта или по правилу левой руки (рис. 6.11). В однородном магнитном поле сила Ампера

F=IBsin, (6.37)

где   угол между проводником и .

6.9. Взаимодействие параллельных токов

Найдем силу взаимодействия двух параллельных проводников с током бесконечной длины в вакууме (= 1, рис. 6.12).

Рис. 6.12

Каждый элемент проводника с током I₁находится в магнитном поле индукции В₂, созданным проводником с токомI₂, и, наоборот, каждый элемент проводника с токомI₂находится в магнитном поле индукции В₁, созданным проводником с токомI₁. Расстояние между проводникамиd.

Индукция магнитного поля проводника с током I₁

(6.38)

По закону Ампера на проводник с током I₂ действует сила

. (6.39)

На основании третьего закона Ньютона (рис. 6.12).

С учетом (6.38) формулу (6.39) перепишем в виде

. (6.40)

Так как проводники бесконечной длины, найдем силу, действующую на единицу длины проводника, в виде

_.(6.41)

Полученную формулу (6.41) используют для определения в Си единицы силы тока  ампера (А).

За единицу силы тока принимают ток, равный 1 А, текущий по двум параллельным бесконечной длины тонким проводам ничтожно малого сечения, находящимися на расстоянии одного метра в вакууме, взаимодействующими между собой с силой 210^7 Н на единицу длины.

Если ток течет по проводам в противоположных направлениях, то они отталкиваются друг от друга.