4. Работа перемещения заряда в электростатическом поле

Поместим пробный, положительный точечный заряд в неоднородное электрическое поле. Будем его перемещать из положения 1 в 2 (рис. 8).

Рис. 8

Весь путь 1  2 представим в виде малых элементов , в пределах которых электрическое поле можно считать однородным ().

Из механики известно, что работа силы

_(15а)

где dr =сos; r₁ и r₂  радиусвекторы начального 1 и конечного 2 перемещений.

На пробный заряд q₀ в электростатическом поле действует кулоновская сила F = q₀E, где Е  напряженность поля, созданного, например, точечным, положительным зарядом q, т. е. . Тогда работа

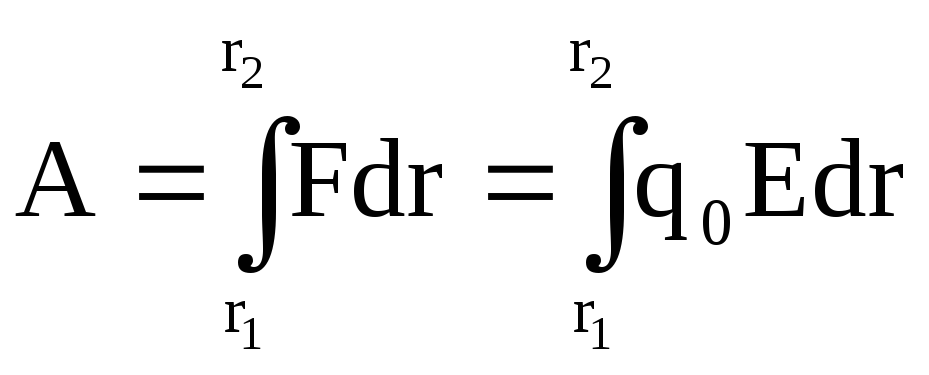или .

После интегрирования имеем

. (16)

Знак работы зависит от знака зарядов q и q₀ и величин r₁ и r₂.

Из (15) следует, что работа на конечном участке 12 произвольного пути перемещения заряда q₀ не зависит от формы пути (траектории), а зависит только от координат начального 1 и конечного 2 перемещений (от радиусвекторов)

Следовательно, кулоновская сила является консервативной (потенциальной), т. е. электростатическое поле является центрально-симметричным и потенциальным. Работа сил потенциального поля равна убыли потенциальной энергии, т. е.

А = W_p1  W_p2 . (17)

Из (16) и (17) следует, что потенциальная энергия взаимодействия зарядов q и q₀ может быть записана в виде

,

где С  постоянная, значение которой выбирается таким, чтобы при удалении пробного заряда в бесконечность (при r ) потенциальная энергия обращалась в нуль (W_р= 0). Таким образом,

(18)

Если электрическое поле создано системой зарядов q₁, q₂, ... , q_n, то полная работа по перемещению в вакууме пробного точечного заряда равна алгебраической сумме работ сил, совершающих перемещение каждого заряда в отдельности:

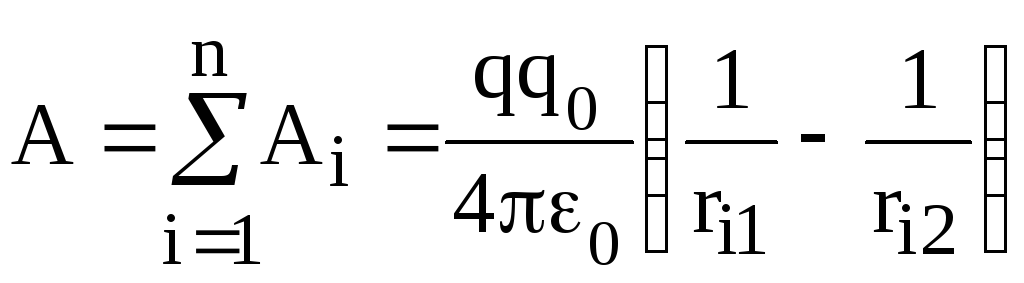, (19)

где r_i1, r_i2  расстояния от заряда q_i до начального и конечного положений пробного заряда q_o.

Следовательно, потенциальная энергия заряда q_o в поле системы зарядов

. (20)

5. Циркуляция вектора

Электростатическое поле является консервативным (потенциальным), следовательно, работа кулоновских сил на замкнутой траектории должна равняться нулю. Действительно, из формулы (16) следует, что работа на замкнутой траектории равна нулю, так как r₁ = r₂.

Если в качестве пробного заряда, переносимого из 1 в 2 данного электростатического поля , взять единичный, положительный заряд (например, в СИ, q_o= +1 Кл), то элементарная работа консервативных кулоновских сил поля при перемещении его на малый отрезок

(21)

Полная работа на всем пути 12

. (22)

Циркуляцией вектора по произвольному замкнутому пути L называют интеграл . Так как на замкнутой траектории работа консервативных кулоновских сил равна нулю, то циркуляция вектора электростатического поля равна нулю, т. е.

(23)

Это положение называют теоремой о циркуляции вектора .

Замечание: справедливо и обратное утверждение: если циркуляция вектора электростатического поля равна нулю, то такое поле является потенциальным.