3. Применение теоремы Гаусса.

3.1. Электрическое поле равномерно заряженной плоскости

Пусть бесконечная плоскость равномерно заряжена с поверхностной плотностью заряда +.

Рис. 3

Из свойств симметрии заряженной плоскости следует, что вектор напряженности электрического поля, созданного этой плоскостью, всюду перпендикулярен ей.

В симметричных точках этого поля вектор равен по модулю и противоположен по направлению. В связи с этим в качестве замкнутой поверхности можно выбрать цилиндрическую (рис. 3). Полный поток вектора пронизывающий

Ф_е = 2ЕS.

Согласно теореме Гаусса

,

где

.

Таким образом,

или

, (13)

где Е_n  проекция вектора на нормаль (, рис. 3).

Если   0, то Е_n  0, т. е. вектор направлен от заряженной плоскости (линии напряженности начинаются на положительных зарядах).

Если   0, то Е_n  0, т. е. вектор форме направлен к заряженной плоскости (линии напряженности оканчиваются на отрицательных зарядах).

Согласно (13) напряженность электростатического поля, созданного равномерно заряженной бесконечной плоскостью, не зависит от расстояния до нее, а поле является однородным справа и слева от плоскости.

3.2. Напряженность электростатического поля двух

разноименно заряженных бесконечно протяженных плоскостей

Пусть две параллельные бесконечно протяженные плоскости заряжены равномерно с поверхностной плотностью заряда  =+  =  .

Рис. 4

Результирующую напряженность электрического поля в этом случае можно найти, используя принцип суперпозиции полей, созданных каждой из заряженных плоскостей в отдельности (рис. 4), где линии напряженности с двумя стрелками соответствуют полю положительно заряженной плоскости, а с одной стрелкой  полю отрицательно заряженной плоскости. В соответствии с рис. 4 слева и справа от плоскостей электрическое поле равно нулю (Е ₊ = Е  = 0).

Между плоскостями линии напряженности направлены в одну сторону, следовательно, с учетом (13) имеем

(14)

Таким образом, электрическое поле между заряженными разноименно бесконечно протяженными плоскостями однородно, за исключением краевых эффектов. Если размеры плоскостей (пластин) много больше расстояния между ними, то полученный результат остается справедливым и для пластин конечных размеров (плоский конденсатор).

3.3. Поле равномерно заряженной сферической поверхности

Рис. 5

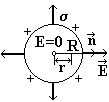
Пусть сферическая поверхность радиуса R заряжена равномерно с поверхностной плотностью заряда +. Электрическое поле заряженной сферы  центральносимметричное. Силовые линии напряженности направлены от поверхности на продолжение радиусов, а модуль вектора должен зависеть только от расстояния r до поверхности сферы. В качестве замкнутой поверхности проще всего использовать концентрическую сферу радиуса r, проходящую через ту точку электрического поля, в которой требуется определить напряженность этого поля.

Рассмотрим три случая:

а) r  R.

Внутри сферы зарядов нет. Все заряды расположены на внешней поверхности сферы, т. е. в любой точке внутри сферы Е = 0 (рис. 5);

б) r  R (рис. 6).

В качестве замкнутой поверхности возьмем концентрическую сферу радиуса r . Найдем напряженность поля, например, в т. Б;

Поток вектора , т. е. Ф_е = Е S_r (Е = Е_n, ),

где S_r = 4r²  площадь сферической поверхности радиуса r.

Рис. 6

Согласно теореме Гаусса поток вектора

,

или

где ;

Рис. 7

S_R = 4R²  площадь сферической поверхности радиуса R.

Таким образом,

Следовательно,

. (15)

Если в формуле (15) поверхностную плотность заряда , заменить на заряд q,

т. е. ,

то

.

Вывод: на любом расстоянии r от заряженной сферы напряженность электрического поля можно найти по формуле напряженности точечного заряда, если весь заряд сферы сосредоточить в ее центре (т. 0);

в) r = R. В этом случае нужно в формуле (15) вместо r запишем R, тогда

или .

График изменения напряженности электрического поля заряженной сферической поверхности от расстояния r приведен на рис. 7.