13

Электричество и магнетизм Н.Ф. Шемяков

Лекция 2

1. Теорема Гаусса в интегральной форме

Рис. 1

Электрическое поле обладает важным свойством: потоком вектора напряженности (потоком вектора ). Для наглядности воспользуемся геометрической картиной описания электрического поля: число силовых линий напряженности равно напряженности электрического поля. Часть силовых линий будет пронизывать элементарную площадку dS, вектор нормали которой составляет угол  с вектором (рис. 1).

Потоком вектора напряженности электрического поля называют интеграл по поверхности от скалярного произведения векторов и dS.

(1)

Элементарный поток вектора напряженности электростатического поля

, (2)

где Е_n  проекция вектора на нормаль .

В замкнутых поверхностях вектор нормали направлен наружу (внешняя нормаль), охватываемой этой поверхностью.

Замечание: понятие потока относится к любому векторному полю.

Рис. 2

Для того чтобы найти поток вектора , окружим точечный заряд произвольной замкнутой поверхностью S (рис. 2).

По определению поток вектора

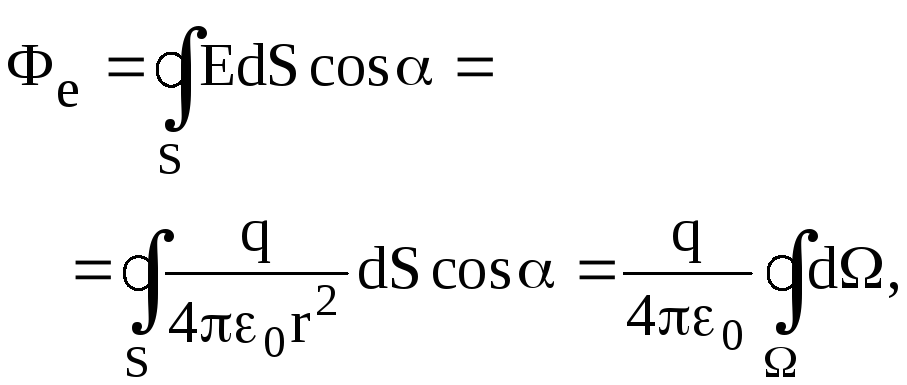(3)

где  телесный угол, опирающийся на элемент dS поверхности S, с вершиной в точке расположения заряда q;  напряженность электрического поля точечного заряда.

Интегрирование (3) по всей поверхности S эквивалентно интегрированию по всему телесному углу  = 4. Следовательно, после интегрирования

. (4)

Если замкнутая поверхность охватывает систему точечных зарядов (как положительных, так и отрицательных) q_1, q_2, ... , q_n, то согласно принципу суперпозиции напряженность результирующего поля

,

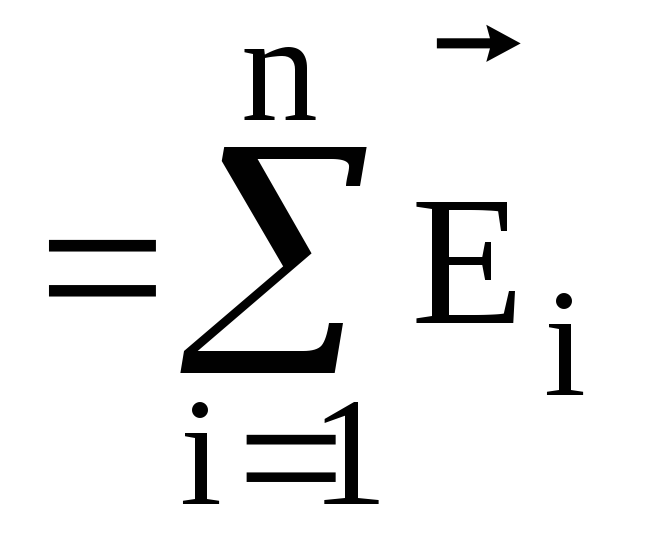где Е_i  напряженность электрического поля i го точечного заряда.

Полный поток вектора напряженности, созданного системой зарядов, запишем в виде

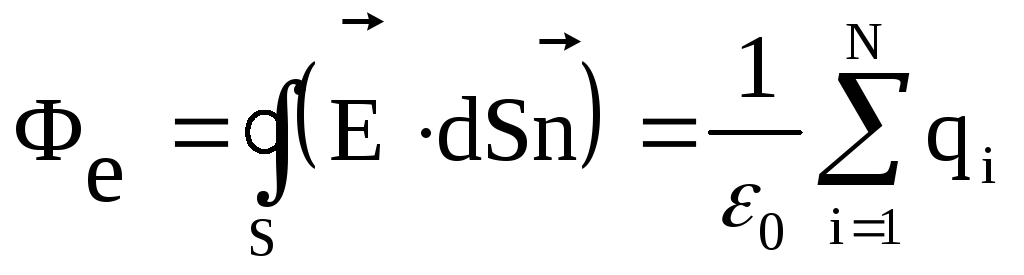(5)

Поток вектора сквозь произвольную замкнутую поверхность, охватывающую заряды, пропорционален алгебраической сумме зарядов.

Если заряды q₁, q₂, ... , q_n находятся вне замкнутой поверхности, то полный поток вектора через эту поверхность равен нулю.

Замечание: напряженность электрического поля зависит от расположения всех зарядов в замкнутой поверхности, а поток вектора останется неизменным.

2. Теорема Гаусса в дифференциальной форме.

Используя формулу объемной плотности заряда, имеем

, (6)

где   среднее значение объемной плотности заряда в объеме V.

Значение q из (6) подставим в (2), предварительно разделив правую и левую части его на объем V:

. (7)

При стягивании объема V в интересующей нас точке поля к нулю (V 0) средняя объемная плотность заряда  будет стремиться к истинному значению  в данной точке электрического поля, т. е. отношение в левой части (7) будет стремиться к .

Величина, являющая пределом отношения 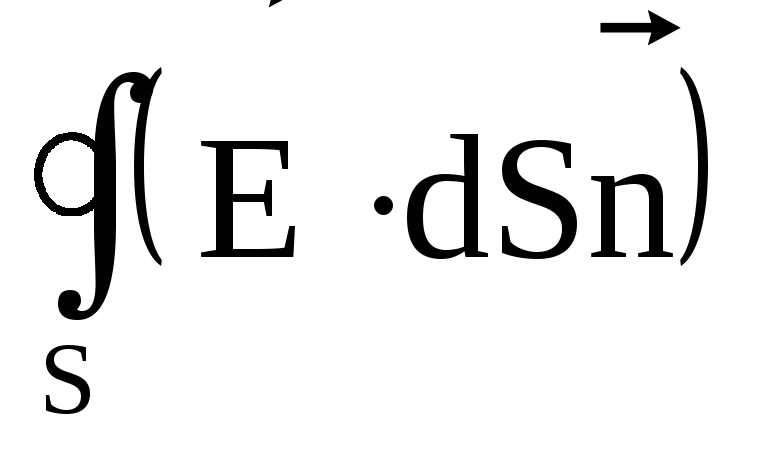кV при V 0, называется дивергенцией поля .

Дивергенцию поля обозначают символом diV, т. е. по определению

. (8)

Согласно (8) дивергенция является скалярной функцией координат.

Для нахождения отношения потока вектора к объему V берут бесконечно малый объем dV и определяют поток вектора ,пронизывающий произвольную замкнутую поверхность, охватывающий объем dV.

В декартовой системе координат

. (9)

Таким образом, при V 0 в формуле (8) его левая часть стремится к diV, а правая к .

Следовательно, . (10)

Формула (10) выражает теорему Гаусса в дифференциальной форме.

Запись формул и действия с ними упрощаются при введении векторного дифференциального оператора

, (11)

где  единичные векторы осей Х, У, Z соответственно.

Векторный дифференциальный оператор приобретает вполне определенный смысл только в сочетании со скалярной или векторной функцией, на которую символически умножается, т. е. теорему Гаусса в дифференциальной форме

=(12)

Теорема Гаусса является локальной, т. е. дивергенция поля в заданной точке этого поля зависит только от объемной плотности электрического заряда.