8

Волновая оптика ___________________________________________________________________________________________________________________________________________________________

Лекция 4

8.7. Разрешающая способность спектральных приборов

а). Призма

Рис. 8.10

Проходя через призму, белый цвет (луч) не только преломляется, но и разлагается в цветной радужный спектр.

Рассмотрим прохождение через призму монохроматического луча света.

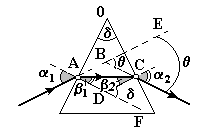
Свет, падающий на призму, с преломляющим углом  и абсолютным показателем преломления n (окружающая среда  вакуум, n_в = 1) проходит через призму, как показано на рис. 8.10.

Используя закон преломления в точках А и С, имеем

Из рис. 8.10 следует, что

 = (₁  ₁) + (₂  ₂);

₁ + ₂ = .

Следовательно,

n (8.41)

 = ₁ + ₂  

Если ₁ = ₂, то угол отклонения светового луча  будет наименьшим.

Во многих оптических приборах применяются отражательные призмы. Для построения хода лучей в них используют закон преломления и явление полного внутреннего отражения.

Световой луч, войдя в призму, испытывает одно или несколько полных внутренних отражений.

Угол, образованный выходящим лучом с выходной гранью призмы, равен углу, образованному входным лучом с входной гранью. Это приводит к тому, что в отражательных призмах не наблюдается разложение белого света на различные цвета.

Это не наблюдается и при прохождении белого света через плоскопараллельную пластинку.

В случае, где рассматривается призма Дове, световые лучи наряду с полным внутренним отражением испытывают два преломления.

При падении белого света на такую призму из нее выйдет набор лучей разного цвета.

Однако из-за параллельности лучей и вследствие того, что световой пучок имеет некоторую ширину, произойдет их сложение (перекрытие) и будет наблюдаться снова белый свет.

Это произойдет в том случае, если ширина пучка d< , где   ширина выходящего пучка из призмы.

При 210^4 м наблюдатель может разрешить (видеть раздельно), например, красный и фиолетовый лучи.

Отражательную призму используют вместо второго зеркала в резонаторе лазера для получения импульсного излучения, если она вращается.

Например, при числе оборотов n = 10³ об/c, совершаемых отражательной призмой, получают световые импульсы длительностью  10^7 с.

Максимальная величина мощности импульса составляет 10⁷ Вт.

Разрешающую способность призмы можно найти по формуле:

 /  =  (₂  ₁) n / , (8.42)

где ₂ и ₁  различные пути хода лучей в призме и при нормальной дисперсии стекла призмы (n /  < 0).

Минимальная разрешающая способность призмы, при которой может быть разрешена двойная D-линия натрия  /   956, если ₂ = 1 см  длина основания призмы; ₁= 0.

б). Оптическая линза

В науке и технике широко используются оптические собирающие и рассеивающие линзы, электронные, магнитные и гравитационные линзы.

Если оптическая линза находится в среде с абсолютным показателем преломления n₁ > 1, то формула линзы записывается в виде

,

где n  абсолютный показатель преломления материала линзы; R₁ и R₂  радиусы кривизны преломляющих поверхностей линзы; F  фокусное расстояние линзы.

Если n₁ = 1, то формула (6.41) принимает более простой вид:

(8.43)

или , (8.43а)

где f  расстояние от предмета до линзы; d  расстояние от изображения до

линзы.

Рис. 8.11

На рис. 8.11, а показан ход лучей в собирающей линзе. На рис. 8.11, б показан ход лучей в рассеивающей линзе.

Угловое расстояние между двумя светящимися точечными объектами можно найти по формуле  = ₁, где ₁ – угловое расстояние двух точечных источников, даваемое идеальной линзой с диаметром объектива линзы D. Величина, обратная  – есть разрешающая способность линзы (оптической системы).

Для телескопа угловое расстояние двух точечных источников можно найти по формуле

₁ =1,22 / D, (8.44)

D – диаметром объектива телескопа.