9.11.2. Линейный магнитооптический эффект Фарадея

Рис. 9.25

Из всех магнитооптических эффектов наибольшее распространение получил линейный по полю эффект магнитного кругового двойного лучепреломления, вызывающий поворот плоскости поляризации линейно-поляризованного света, распространяющегося через вещество вдоль магнитного поля.

Используя двойное лучепреломление, можно не только получать плоскополяризованный свет, но и управлять поляризацией света.

Например, пусть световой пучок нормально падает на пластинку одноосного кристалла, оптическая ось которого перпендикулярна пучку света (рис. 9.25).

Оптическая ось ОО пластинки составляет с электрическим вектором ₁ падающего луча угол /2.

Разложим вектор ₁ на составляющие: вектор ₀₁ и вектор _е1, соответствующие обыкновенному и необыкновенному лучам.

Эти лучи распространяются по одному направлению, но скорости обыкновенной v₀ и необыкновенной v_е волн различны (для исландского шпата v₀ > v_е).

Поэтому будут различными и длины волн для обыкновенного и необыкновенного лучей.

Длины волны обыкновенного и необыкновенного лучей

. (9.20)

Если толщину пластинки d подобрать такой, чтобы укладывающееся на ней число d / ₀ обыкновенных длин волн было больше укладывающегося на ней числа необыкновенных длин волн d / _e на 0,5, то получим

 = 0,5 (9.21)

В этом случае взаимная ориентация векторов ₀₂ и _е2 на выходе пластинки будет такой, что результирующий вектор

₂ =₀₂ + _е2

окажется повернутым относительно оптической оси на тот же угол , но в противоположную сторону, чем вектор₁.

Поэтому, вектор ₂ повернут относительно вектора ₁ на угол .

Рассматриваемую пластинку называют полуволновой, так как в ней оптическая разность хода обыкновенной и необыкновенной волн равна половине длины волны.

А сдвинуты они по фазе относительно друг друга на  радиан.

Из (9.20) и (9.21 ) найдем толщину пластинки:

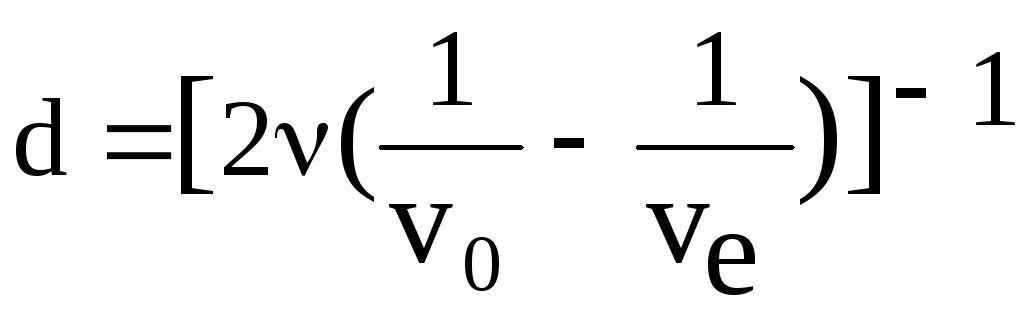. (9.22)

Например, при  = 4,510¹⁴ Гц (красный свет) для исландского шпата имеем

v₀ = 1,8110⁸ , v_е = 2,0210⁸ 

Тогда d = 210^6 м.

Полученный результат соответствует минимальной толщине полуволновой пластинки из исландского шпата.

Толщина реальной полуволновой пластинки может быть в 2N + 1 раз больше d, где N  целое число.

В квантовой теории оптически активных веществ рассматриваются процессы, связанные с конечным размером молекул (10^10 м).

Для объяснения оптической активности необходимо учитывать взаимодействие электрических и магнитных дипольных моментов, наведенных в молекулах полем проходящей волны.

Теория оптической активности молекулярных сред, активных лишь в кристаллической фазе, тесно связана с теорией экситонов (квазичастиц), так как оптическая активность таких веществ определяется характером волн поляризации в этих кристаллах.