5.5. Туннельный эффект

При описании движения классической частицы в потенциальном “ящике “ считается, что частица может покинуть потенциальный “ящик” или проникнуть в него, если ей сообщить энергию, равную или большую разности высоты потенциального барьера и ее собственной энергии. Квантовая механика допускает вероятность прохождения частицы сквозь потенциальные барьеры при меньших значениях ее энергии по сравнению с энергией потенциального барьера. Такое явление получило название туннельного эффекта.

Пусть квантовая частица с массой m движется вдоль оси Х слева направо. Сталкиваясь с потенциальным барьером высотой W_po:

причем энергия частицы W меньше высоты потенциального барьера W_po.

При х > 0, т. е. в области, в которую не способна проникнуть не квантовая частица уравнение Шредингера имеет вид

Решениями этого уравнения являются две экспоненты:

(х)  , где.

Экспонента с положительным показателем физического смысла не имеет и должна быть исключена, т. к. предсказывает неограниченный рост вероятности обнаружения частицы за барьером с увеличением глубины проникновения х.

Следовательно, при х > 0 частица с энергией W < W_po имеет волновую функцию, которая изменяется как (х) .

Это значит, что при х > 0 координаты частицы распределены с плотностью вероятности ],

где w(0) равно значению величины (х)² при х = 0.

Следовательно, с увеличением глубины проникновения х частицей плотность вероятности W(x) убывает экспортенциально. Причем убывание происходит тем быстрее, чем больше разность (W_po  W).

Таким образом, на глубине проникновения

плотность вероятности W(x) уменьшается в е раз.

Например, для электрона (m = 9,1110^31 кг), для которого W_po  W 10^-3 эВ= = 1,610^22 Дж, глубина проникновения х₀  10^9 м = 10 Å . На такие расстояния удаляются от поверхности металла электроны проводимости, энергия которых 10^3 эВ меньше глубины потенциальной ямы, удерживающей электроны внутри металла (потенциальная яма создается взаимодействием электронов с положительными ионами кристаллической решетки металла).

Рис. 5.4, а

Явление туннельного эффекта (подбарьерное прохождение) характеризуется коэффициентом прозрачности D потенциального барьера. Прозрачность барьера зависит от “формы” и высоты потенциального барьера. Например, если потенциальный барьер  прямоугольный высотой W_ро и шириной d (рис. 5.4, а), то его прозрачность

D =D₀exp(), (5.27)

где h  постоянная Планка; m  масса частицы; W  полная энергия частицы; D₀  постоянный коэффициент, близкий к единице. Вероятность туннелирования частицы (5.27), тем меньше, чем больше ширина барьера и чем меньше полная энергия налетающей частицы. Проницаемость барьера уменьшается и с увеличением массы частицы. Если барьер не прямоугольный и его высота зависит от координаты и медленно изменяется (рис. 5.4, б), то прозрачность барьера

D = D₀exp (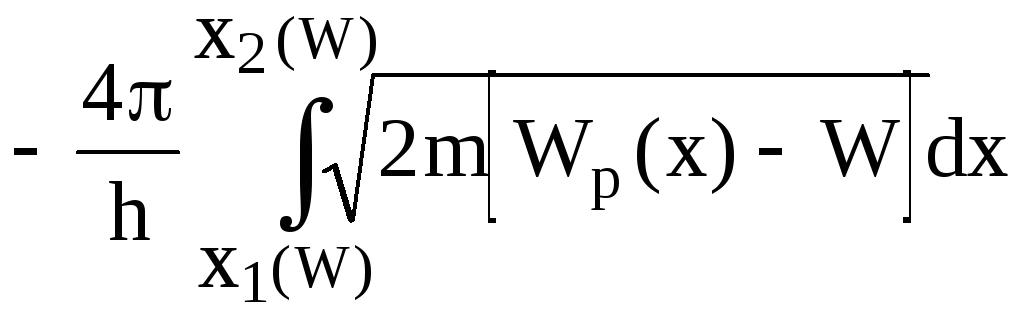), (5.28)

где в точках х₁(W) и х₂(W) начала и конца потенциального барьера

W = W_p(x).

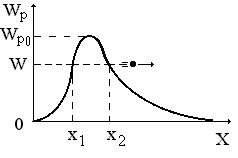
Прохождение частицы сквозь потенциальный барьер возможно благодаря существова6ию под барьером волновой функции, "прокладывающей" путь частице вплоть до точки х₂ (рис. 5.4, б) и правее этой точки, т. е. приводит к возможности обнаружить ее в области, запрещенной классической физикой.

Если полная энергия частицы W меньше высоты потенциального барьера W_p, то в области, где W_p(x) > W, кинетическая энергия частицы (W_k = p² / 2m) отрицательна, т. к. W = W_k+ W_p(x).

Рис. 5.4, б

С классической точки зрения эта область недоступна для такой частицы, т. к. невозможно существование мнимой кинетической энергии (мнимого импульса). Квантовая механика допускает возможность обнаружить частицу в этой области (парадокс туннельного эффекта).

Однако здесь нет парадокса и рассуждения о мнимом импульсе частицы неверны, т. к. туннельный эффект чисто квантовое явление.

В классической физике W = W_k+ W_p(x), т. е. можно одновременно определить кинетическую и потенциальную энергии с высокой степенью точности (W_p зависит от координаты, W_k  от импульса). В квантовой механике согласно соотношениям неопределенностей Гейзенберга нельзя одновременно точно определить импульс и координату (или потенциальная W_p и кинетическая W_k энергии частицы не могут быть одновременно определены точно). Следовательно, равенство W= W_k+ W_p(x) в квантовой механике применять нельзя. В квантовой механике движение частицы описывается волновой функцией (x, y, z, t). В случае одномерного движения частицы при фиксировании ее в определенной области х следует, что глубина проникновения ее в классически запрещенную область внутри потенциального барьера

. (5.29)

Поэтому изменение импульса частицы

. (5.30)

Тогда, изменение кинетической энергии

. (5.31)

Следовательно, изменение кинетической энергии превышает величину энергии, недостающей частице, находящейся внутри потенциальной ямы для того, чтобы она могла “классическим “ способом покинуть потенциальную яму. Проявление туннельного эффекта обнаружено в явлениях: распада радиоактивных ядер, холодной эмиссии электронов, примесной проводимости полупроводников, в эффекте Джозефсона и т. д. Аналогом туннельного эффекта в волновой оптике служит проникновение световой волны внутрь отражающей среды (на расстояние порядка длины волны света) в условиях, когда с точки зрения геометрической оптики происходит полное внутреннее отражение.