5.4. Квантовый гармонический осциллятор

В квантовой механике задача о колебании квантового осциллятора решается с помощью уравнения Шредингера

.

Стационарные состояния квантового осциллятора описываются такими решениями уравнения Шредингера, которые быстро убывают при  х , т. к. на сколь угодно больших расстояниях потенциальная энергия частицы W_p(x) массы m, совершающей колебания с циклической частотой , например, вдоль оси Х равна W_p(x) = m²x²/2. (5.20)

Введем обозначения: =, а₂ =.

С учетом этого уравнение Шредингера принимает вид

.

После введения новой переменной имеем.

Тогда уравнение Шредингера

или . (5.21)

Решения уравнения (5.21) имеют место лишь при определенных значениях параметра , а именно= 2v +1, (5.22)

После подстановки значений а₁ и а₂ в (5.22) имеем . (5.23)

Поэтому значения энергии квантового осциллятора можно найти по формуле

. (5.24)

Из формулы (5.24) следует: энергия осциллятора W_n квантована и может принимать дискретные значения (v = 0, 1, 2, ... – колебательное квантовое число).

Энергетический спектр волновых функций квантового осциллятора приведен на рис. 5.4, где по оси абсцисс отложено расстояние частицы от положения равновесия. Кривая (параболическая яма) изображает потенциальную энергию частицы.

В этом случае частица с любой энергией (как и в случае потенциальной ямы с бесконечными стенками) “заперта” внутри потенциальной ямы и спектр ее энергии дискретен. Горизонтальные прямые изображают энергетические уровни частицы.

Энергия низшего основного уровня  наименьшее значение энергии, совместимое с соотношениями неопределенностей Гейзенберга [положение частицы на дне ямы (W = 0) означало бы точное равновесие, при котором координата х = 0 и импульс р = 0, что не возможно согласно соотношениям неопределенностей]. Энергия v  го уровня

. (5.25)

Каждому состоянию соответствует своя волновая функция. В энергетическом спектре (5.25) расстояния между соседними уровнями W = W_n+1  W_n не зависят от колебательного квантового числа v и равны между собой. Такое расположение уровней в энергетическом спектре называют эквидистантным.

Рис. 5.4

Дискретный характер уровней энергии позволяет понять, почему в определенных условиях заведомо сложные, составные системы (например, атомы или молекулы) ведут себя как элементарные частицы (бесструктурные). Причина состоит в том, что основное состояние связанной системы отделено от первого возбужденного состояния энергетическим интервалом (энергетической щелью). Такая ситуация характерна для атомов, молекул, ядер и др. квантовых систем.

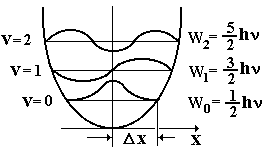
Благодаря энергетической щели внутренняя структура квантовых систем не проявляется до тех пор, пока обмен энергией при ее взаимодействии с другими системами не превысит значения, равного ширине энергетической щели. Поэтому при достаточно малом обмене энергией сложная квантовая система (например, атом или ядро) ведет себя как бесструктурная частица (материальная точка). Так, при энергиях теплового движения, меньших энергии возбуждения атома, атомные электроны не могут участвовать в обмене энергией и не дают вклада в теплоемкость. При v >> 1, (v + 1/2)  v энергетические уровни совпадают со значениями энергии осциллятора , использовал Планк. Согласно классической теории приv = 0, W_n= 0 осциллятор не колеблется и находится в положении равновесия.

Считая атомы твердого тела трехмерными осцилляторами из классической физики следует, что при Т = 0 К атом должен покоиться.

Согласно квантовой теории наименьшая энергия, которую имеет гармонический осциллятор при Т = 0 К не равна нулю, т. е.

. (5.26)

Эта нулевая энергия не может быть отнята у осциллятора никаким охлаждением, даже при Т = 0 К. Наличие нулевой энергии при абсолютном нуле температуры, когда квантовая система (атом) совершает “нулевые колебания” было подтверждено опытами по рассеянию света кристаллами при Т  0 К.

Такой вывод подтверждается и соотношениями неопределенностей Гейзенберга. Наличие “нулевой энергии” позволяет объяснить, почему гелий является единственным веществом, существующим в жидком состоянии при Т0 К? Это обусловлено тем, что у гелия частота колебаний атомов ₀ довольно велика изза малой массы атома гелия (2₀ = ₀ ). С другой стороны силы притяжения атомов гелия малы из-за полной застройки электронных оболочек.

Поэтому атомы гелия при Т 0 К совершают довольно интенсивные колебания, что позволяет гелию оставаться в жидком состоянии, т. е. это чисто квантовый эффект. Существенным отличием _кв от _кл является возможность обнаружить частицу за пределами классически запрещенной области (изза туннельного эффекта).