5.2. Движение квантовой частицы

в стационарном силовом поле

Простым видом движения квантовой частицы является свободное движение. Потенциальная энергия частицы в этом случае обращается в ноль, т. е. W_p(x) = 0.

Для свободной частицы, движущейся, например, вдоль оси Х, стационарное уравнение Шредингера

или

(5.10)

Функция (х) = Ае^ikx, где А = соnst и k = const, является частным решением этого уравнения с энергией

W = h²k²/(8²m). (5.11)

В общем случае для зависящей от времени волновой функции получаем

(x, t) = Ae^{-it |+ikx}. (5.12)

Это решение представляет собой плоскую монохроматическую волну с циклической частотой  и волновым числом k, которая называется волной де Бройля.

Координаты свободной квантовой частицы распределены с плотностью вероятности

w(x) = (х)² = A² = const.

Так как плотность вероятности постоянна, то существует одинаковая вероятность обнаружить свободную частицу в любых точках пространства, т. е. область движения свободной частицы неограниченно велика, что естественно.

Согласно корпускулярно-волновому свойству частиц

 = 2W / h;  = W / h, k = 2p / h,

где р  импульс частицы.

Тогда волна де Бройля запишется в виде:

(x, t) = A exp(2iWt / h + 2ipx / h). (5.13)

Причем зависимость энергии частицы от импульса оказывается обычной для нерелятивистских частиц:

W(p) = p² / 2m.

Таким образом, энергетический спектр свободной квантовой частицы (не путать со спектрами испускания или поглощения атома), которая при р  0 является простейшей квантовой системой с неограниченной областью движения, непрерывен и ограничен снизу значением энергии W = 0.

5.3. Одномерное движение электрона в потенциальном ящике

Примером движения электрона в потенциальном ящике является движение коллективизированных электронов в металлах.

В этом случае энергия электрона вне и внутри потенциального ящика имеет следующие значения:

W_p= 0 при 0  x  , W_p=  при x  0 и x  , (5.14)

где  ширина потенциального ящика.

Согласно классической теории вне металла потенциальная энергия электрона равна нулю, т. е. W_p = 0, а внутри металла она отрицательна и численно равна работе выхода электрона из металла (W_p = А_в).

Рис. 5.2

Следовательно, движение электрона ограничено потенциальным барьером прямоугольной формы с плоским дном (рис. 5.2).

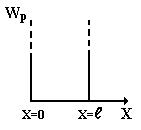
Для квантового описания движения электрона в таком потенциальном ящике применим стационарное уравнение Шредингера

.

Это уравнение имеет решение, если волновая функция (х) обращается в нуль на стенках ящика, т. е.

(0) = () = 0.

Тогда . (5.15)

В области значений 0  x  W_p = 0, а отношение имеет конечное значение (). При х 0 и х  W_p  , тогда (х)  0.

Следовательно, для электрона, находящегося в потенциальном ящике с бесконечно высокими стенками, уравнение Шредингера должно быть таким, чтобы  = 0 и ² = 0 вне области значений 0  x  , т. е. вероятность найти электрон вне ящика равна нулю (без учета туннельного эффекта).

Решая уравнение

или (5.16)

(,k =  волновое число) получаем, что при х = 0 волновая функция  = 0, а при x =  () = 0.

Таким образом, решение уравнения (8.40) можно записать в виде

или (х) =А₁coskx + A₂sinkx, (5.17)

где А₁ и А₂  некоторые постоянные, определяются из условия нормировки.

При х = 0 из (5.17) следует, что А₁= 0; при x = имеем () = А₂sink

или А₂0, А₁=0, sink=0. (5.18)

Из (5.18) следует, что величина k должна принимать дискретные значения k_n, удовлетворяющие условию k_n = n, где n =1, 2, 3, ... , т. е. .

Так как k_n = 2 / _n, где _n  длина волны де Бройля для электрона в потенциальном ящике, значит или.

Рис. 5.3

Следовательно, на длине потенциального ящика должно укладываться целое число волн де Бройля.

Выражая энергию через волновое число, найдем энергетический спектр частицы в глубокой потенциальной яме, т. е.

W_n = h²k_n²/(8²m) = h²n²/(8²m). (5.19)

Энергетический спектр частицы в глубокой потенциальной яме изображен на рис. 5.3. Видно, что он дискретен и ограничен снизу.

Следовательно, энергия электрона в потенциальном ящике может принимать лишь ряд дискретных собственных значений энергии W_n.

Это значит, что энергия электрона в потенциальном ящике является квантованной, а значения W_n называются уровнями энергии, где n = 1, 2, 3, …  главное квантовое число, определяющее вид волновой функции и энергию частицы в состоянии с этой волновой функцией.

В энергетическом спектре частицы (5.19) при n = 1 основной уровень имеет энергию W₁ = h²/(8²m) >0.

Это неравенство означает невозможность остановки частицы, т. к. ее кинетическая энергия не может быть меньше W₁.

Согласно соотношений неопределенности Гейзенберга неопределенность импульса частицы р не может быть меньше величины

Но в потенциальной яме шириной положение частицы определено с точностью х  . Следовательно, хр  h / (2), что находится в полном согласии с квантовой механикой.

При больших значениях n квантовая механика дает значения энергии, близкие по величине к результатам классической физики.

В этом проявляется принцип соответствия Бора: при больших квантовых числах выводы и результаты квантовой механики должны соответствовать результатам классической физики, т. е. в предельном случае квантовая механика переходит в классическую теорию.