14

Квантовая физика

___________________________________________________________________________________________________________________________________________________________0

Лекция 11

5. Уравнение шредингера

5.1. Временное и стационарное уравнения Шредингера

Любое состояние микрочастицы в квантовой механике определяется волновой функцией (амплитудой вероятности).

В нерелятивистском случае уравнением движения микрочастицы является временное уравнение Шредингера

(5.1)

где

 оператор Лапласа; i =  мнимая единица; h  постоянная Планка; W_p(x, y, z, t)  потенциальная энергия частицы в силовом поле; m  масса частицы;  = (х, у, z, t) = (r, t)  волновая функция частицы; r = (х, у, z)  пространственная координата и время t.

Справедливость уравнения Шредингера (оно постулируется, а не выводится) доказывается тем, что выводы квантовой механики, полученные на основании этого уравнения в атомной и ядерной физике, находятся в полном согласии с экспериментальными данными.

Стационарное уравнение Шредингера имеет вид

, (5.2)

где W = const  полная энергия частицы.

Уравнение (5.2) справедливо для любой квантовой частицы движущейся со скоростью v < c и характеризуется следующими свойствами:

1. функция  должна быть однозначной, непрерывной, конечной;

2. производные  непрерывны;

3. функция ²  должна иметь конечный интеграл.

Волновое уравнение Шредингера (волн де Бройля) имеет аналогичный вид, как и все волновые уравнения любой физической природы.

Таким образом, электрон в атоме существует не в виде частицы, а в виде волны де Бройля (волны вероятности).

Движение электрона (любой другой микрочастицы) должно подчиняться волновому уравнению Шредингера.

В случае движения частицы вдоль оси Х волна де Бройля имеет вид плоской волны:

, (5.3)

где W_p(x)  потенциальная энергия взаимодействия электрона и ядра, удаленные на расстояние х.

Из классической физики следует, что уравнение колебаний, например, струны, описывается формулой

или

, (5.4)

где

 волновое число; ₀  собственная циклическая частота колеблющейся системы.

Некоторые решения уравнения (5.4) [функции s(x)] приведены на рис. 5.1, а. Графики имеют вид синусоид, и смысл их очевиден: они изображают форму струны в какой-то момент времени, т. е. моментальную фотографию процесса ее колебаний.

Форма колебаний струны определяется числом узлов k, т. е. числом точек, остающихся неподвижными в процессе колебания.

Им соответствует бесконечный набор решений s(x), которые различаются только числом узлов.

Уравнение Шредингера (5.3) можно представить в виде

, (5.5)

где . (5.6)

Следовательно, по форме уравнение (5.5) мало отличается от уравнения струны (5.3).

Если электрон движется свободно, то W_p(x) = 0, поэтому его полная энергия W = W_k, и следовательно, длина волны электрона постоянна:

и равняется длине волны де Бройля.

В этом случае уравнение Шредингера в точности совпадает с уравнением струны.

а

б

Рис. 5.1

При движении электрона в атоме он взаимодействует с ядром (например, с протоном в атоме водорода) по закону Кулона и его потенциальная энергия

, (5.7)

где е  элементарный заряд, равный заряду протона и электрона (по модулю).

В этом случае длина волны де Бройля

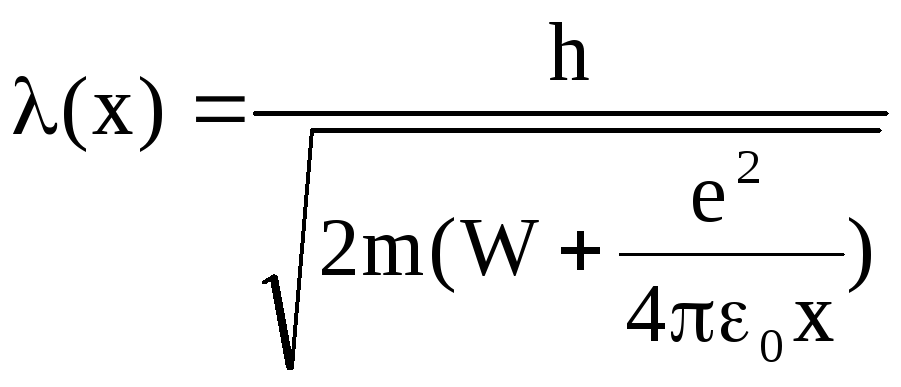(5.8)

не имеет определенного значения и меняется от точки к точке.

Несколько решений уравнения (5.5), т. е. функции _n(x), изображено на рис. 5.1, б, где n = 1, 2, 3, ...  главное квантовое число, характеризующее энергию электрона в атоме.

В теории колебаний струны возникает такой случай: если колеблется струна со всевозможными грузами и утолщениями на ней, то ее колебания описываются аналогичным волновым уравнением.

Таким образом, уравнение Шредингера имеет решение не всегда, а только при определенных значениях энергии W_n, которым соответствуют собственные функции _n(x), зависящие от n.

Дискретные значения энергии W_n стационарных состояний электрона в атоме, характеризуются квантовым числом n, т. е.

,

где ₀  электрическая постоянная; Z  порядковый номер элемента в периодической системе Д.И. Менделеева; m  масса электрона; е  заряд электрона.

Согласно квантовой механике атом не имеет определенных размеров, который определяется состоянием электронов в атоме.

Положение электрона в атоме подчиняется вероятностным законам.

Электрон в атоме представляется в виде электронного облака, и где он находится, в данный момент времени точно указать нельзя, т. е. понятие орбиты в квантовой механике не имеет смысла.

Причина устойчивости атома заключается в его движении и неизменности квантовомеханических законов, управляющих этим движением.

Причем квантовая устойчивость атома значительно надежнее, чем динамическая устойчивость классической механики, так как разрушенный атом восстанавливает свою структуру.

Вывод: Каждая квантовомеханическая система характеризуется своим энергетическим спектром.

В зависимости от вида потенциальной энергии (т. е. от характера взаимодействия в системе) энергетический спектр может быть либо дискретным (как у свободной частицы), либо смешанным (например, энергетические уровни атома при энергиях возбуждения, меньших энергий ионизации, дискретны, а при больших энергиях  непрерывны).

Характер квантовомеханического движения можно понять на примере одномерного движение частицы (например, вдоль оси X) в случае, когда потенциальная энергия W_p зависит только от координаты х.

Уравнение Шредингера (5.5) сводится к уравнению

, (5.9)

где выражение

р²(х) = 2m[W  W_p(x)]

совпадает с формулой квадрата классического импульса частицы в точке с координатой х.

Таким образом, волновая функция и является той величиной, которая позволяет отыскать все вероятности.

Из всех квантовых вероятностей в учебном пособии используется только одна, которая описывает распределение координат частиц.

Для одномерного движения:

вероятность нахождения частицы в интервале (х, х + dx) в момент времени t равна

(х, t)²dx,

где

(х, t)² = ^* (х, t) (х, t)

 квадрат модуля волновой функции

[^* (х, t)  комплексное сопряжение волновой функции  (х, t)].

С помощью волновой функции  (х, t) среднее значение координаты определяется по формуле

.