
- •Часть 1.
- •Потенциальная энергия в поле тяготения Земли
- •О физическом смысле понятия потенциальной энергии
- •21. Гравитационная энергия взаимодействия многих частиц.
- •22. Собственная гравитационная энергия тел. Гравитационная
- •Чёрные дыры
- •23. Теорема о распределении потенциальной и кинетической энергии (теорема о вириале). Пример использования теоремы : оценка средней температуры Солнца.
- •24. Движение планет. Законы Кеплера. Движение нижних планет
- •[Править]Движение верхних планет
- •Законы Кеплера
- •[Править]Первый закон Кеплера (закон эллипсов)
- •[Править]Второй закон Кеплера (закон площадей)
- •[Править]Третий закон Кеплера (гармонический закон)
- •25. Простые задачи нерелятивистской динамики: груз на пружине в
- •26. Космические скорости.
- •27. Движение в неинерциальных системах. Принцип эквивалентности.
- •28. Соударение тел. Упругий и неупругий удар.
- •29. Движение тела переменной массы. Уравнение Мещерского, уравнение Циолковского.
- •30. Закон сохранения момента импульса.
28. Соударение тел. Упругий и неупругий удар.
Абсолютно
упругий удар —
модель соударения, при которой полная
кинетическая энергия системы сохраняется.
В классической
механике при
этом пренебрегают деформациями тел.
Соответственно, считается, что энергия
на деформации не теряется, а взаимодействие
распространяется по всему телу мгновенно.
Хорошей моделью абсолютно упругого
удара является столкновение бильярдных
шаров или упругих мячиков. Математическая
модель абсолютно упругого удара работает
примерно следующим образом:![]()
Абсолю́тно неупру́гий удар — удар, в результате которого компоненты скоростей тел, нормальные площадке касания, становятся равными. Если удар был центральным (скорости были перпендикулярны касательной плоскости), то тела соединяются и продолжают дальнейшее своё движение как единое тело.
![]()
29. Движение тела переменной массы. Уравнение Мещерского, уравнение Циолковского.
Уравнение Мещерского — основное уравнение в механике тел переменной массы, полученное И. В. Мещерским для материальной точки переменной массы (состава)
Уравнение обычно записывается в следующем виде:
![]() ,
,
где:
m — масса материальной точки переменной массы, меняющаяся за счет обмена частицами с окружающей средой;
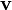 —
скорость движения материальной
точки переменной массы;
—
скорость движения материальной
точки переменной массы;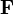 —
внешние силы, действующие на материальную
точку переменной массы со
стороны ее внешнего окружения (в том
числе, если такое имеет место, и со
стороны среды, с которой она обменивается
частицами, например электромагнитные
силы — в случае массообмена с
магнитной средой, сопротивление среды
движению и т. п.);
—
внешние силы, действующие на материальную
точку переменной массы со
стороны ее внешнего окружения (в том
числе, если такое имеет место, и со
стороны среды, с которой она обменивается
частицами, например электромагнитные
силы — в случае массообмена с
магнитной средой, сопротивление среды
движению и т. п.);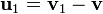 —
относительная скорость присоединяющихся
частиц;
—
относительная скорость присоединяющихся
частиц;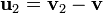 —
относительная скорость отделяющихся
частиц;
—
относительная скорость отделяющихся
частиц;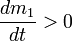 ,
, 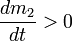 —
скорости массообмена присоединяющихся
и отделяющихся частиц;
—
скорости массообмена присоединяющихся
и отделяющихся частиц;
Формула Циолковского определяет скорость, которую развивает летательный аппарат под воздействием тяги ракетного двигателя, неизменной по направлению, при отсутствии всех других сил. Эта скорость называется характеристической.
![]() ,
,
где:
![]() —
конечная (после выработки всего топлива)
скорость летательного
аппарата;
—
конечная (после выработки всего топлива)
скорость летательного
аппарата;
![]() — удельный
импульс ракетного
двигателя (отношение тяги двигателя к
секундному расходу массы топлива);
— удельный
импульс ракетного
двигателя (отношение тяги двигателя к
секундному расходу массы топлива);
![]() —
начальная масса летательного аппарата
(полезная нагрузка + конструкция аппарата
+ топливо).
—
начальная масса летательного аппарата
(полезная нагрузка + конструкция аппарата
+ топливо).
![]() —
конечная масса летательного аппарата
(полезная нагрузка + конструкция);
—
конечная масса летательного аппарата
(полезная нагрузка + конструкция);
30. Закон сохранения момента импульса.
Зако́н сохране́ния моме́нта и́мпульса (закон сохранения углового момента) — один из фундаментальных законов сохранения. Математически выражается через векторную сумму всех моментов импульса относительно выбранной оси для замкнутой системы тел и остается постоянной, пока на систему не воздействуют внешние силы. В соответствии с этим момент импульса замкнутой системы в любой системе координат не изменяется со временем.
Закон сохранения момента импульса есть проявление изотропности пространства относительно поворота.
В упрощённом виде: ΣL(вектор)=const ,если система находится в равновесии.
