Потенциальная энергия в поле тяготения Земли

Потенциальная энергия в поле тяготения Земли вблизи поверхности приближённо выражается формулой:

где —масса тела, —ускорение свободного падения, — высота положенияцентра масс тела над произвольно выбранным нулевым уровнем.

О физическом смысле понятия потенциальной энергии

• Потенциальная энергия характеризует как минимум два тела или положение тела во внешнем поле.

• Кинетическая энергия характеризуется скоростью; потенциальная — взаиморасположением тел.

• Основной физический смысл имеет не само значение потенциальной энергии, а её изменение.

16) Потенциальная энергия зависит от положения тела. В зависимости от того, куда мы будем (чуть-чуть) смещаться от данной точки, потенциальная энергия будет либо уменьшаться, либо увеличиваться. Вот здесь и живет связь между потенциальной энергией и силой. Сила показывает направление, в котором потенциальная энергия уменьшается быстрее всего, а величина силы определяется скоростью изменения. Другими словами, сила - градиент потенциальной энергии.

F = -grad(U) Где F - консервативная сила, U - потенциальная энергия.

Поле может быть любым, например гравитаионное или электрическое или еще какое... Хоть растянутая пружина. А чем не поле? Ну да, искусственно созданное и одномерное, но поле! Так вот, потенциальная энергия (обозначим U) - это полная работа против сил этого самого поля. Соответственно сила (F) - это производная от потенциальной энергии по перемещению со знаком -. Ну или без знака, если речь идет о скалярном значении поля. F = -(dU/dx).

17) Гравитацио́нный потенциа́л — скалярная функция координат и времени, характеризующая гравитационное поле в классической механике. Имеет размерность квадрата скорости, обычно обозначается буквой . Гравитационный потенциал равен отношениюпотенциальной энергии материальной точки, помещённой в рассматриваемую точку гравитационного поля, к массе этой точки. Впервые понятие гравитационного потенциала ввёл в науку Адриен Мари Лежандр в конце XVIII века.

В современных теориях гравитации роль гравитационного потенциала играют обычно тензорные поля. Так, в стандартной в наше время теории гравитации — общей теории относительности — роль гравитационного потенциала играет метрический тензор.

Гравитационный потенциал и уравнения движения

Движение частицы в гравитационном поле в классической механике определяется функцией Лагранжа, имеющей в инерциальной системе отсчета вид:

, где: —масса частицы, —координата частицы, — потенциалгравитационного поля.

Подставляя выражение для лагранжиана L в уравнения Лагранжа:

,

получаем уравнения движения

.

Гравитационный потенциал и принцип эквивалентности

Уравнения движения частицы в гравитационном поле в классической механике не содержат массы или другой величины, характеризующей частицу. Это является выражением основного свойства гравитационного поля — принципа эквивалентности.

Гравитационный потенциал точечной частицы и произвольного тела

Гравитационный потенциал точечной частицы равен: , где—гравитационная постоянная, —масса частицы, — расстояние от частицы. Эта же формула справедлива и для гравитационного потенциала любого тела со сферически-симметричным распределением плотности массы внутри него.

Для тела с произвольным распределением плотности массы гравитационный потенциал удовлетворяетуравнению Пуассона: , где—оператор Лапласа, — объёмная плотность распределения массы в рассматриваемой точке. Общее решение этого уравнения имеет вид:где r — расстояние от элемента объёма dV до рассматриваемой точки поля, а интегрирование производится по всему объёму тел, создающих поле. Гравитационный потенциал симметричного тела симметричен.

Гравитационный потенциал и потенциальная энергия

Потенциальная энергия частицы в гравитационном поле равна ее массе, умноженной на потенциал поля. Для потенциальной энергии любого распределения масс справедливо выражение:

где — плотностьмассы тела, — гравитационный потенциал,— объём тела.

Гравитационный потенциал постоянного гравитационного поля

Формула для гравитационного потенциала произвольного тела имеет вид:

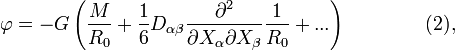
где — полнаямасса системы, а величины:

можно назвать тензором квадрупольного момента масс. Он связан с обычным тензором моментов инерции

очевидными соотношениями

Гравитационный потенциал планет

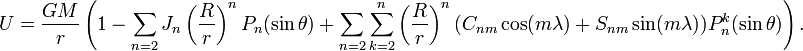
Гравитационный потенциал и гравитационная энергия тела

Гравитационная энергия тела получается интегрированием выражения (1) по объёму тела с использованием выражения для потенциала (2). Для шара массы m, радиусом a, с равномерным распределением плотности масс, получается значение U гравитационной энергии тела:

Гравитационный потенциал и общая теория относительности

В общей теории относительности для случая слабых стационарных гравитационных полей устанавливается связь между компонентом метрического тензора пространства-времени и значением гравитационного потенциала Относительное замедление хода времени в точке с меньшим значением гравитационного потенциала по сравнению с временем в точке с большим значением гравитационного потенциала равно разности гравитационных потенциалов в этих точках, делённой на квадрат скорости света.

Градие́нт (от лат. gradiens, род. падеж gradientis — шагающий, растущий) — вектор, своим направлением указывающий направление наискорейшего возрастания некоторой величины , значение которой меняется от одной точки пространства к другой (скалярного поля), а по величине (модулю) равный быстроте роста этой величины в этом направлении.

Например, если взять в качестве высоту поверхности Земли над уровнем моря, то её градиент в каждой точке поверхности будет показывать «направление самого крутого подъёма», и своей величиной характеризовать крутизну склона.

С математической точки зрения градиент — это производная скалярной функции, определенной на векторном пространстве.

Пространство, на котором определена функция и её градиент, может быть, вообще говоря, как обычным трёхмерным пространством, так и пространством любой другой размерности любой физической природы или чисто абстрактным.

Термин впервые появился в метеорологии, а в математику был введён Максвеллом в 1873 г. Обозначение grad тоже предложил Максвелл.

Стандартные обозначения:

или, с использованием оператора набла,

— вместо может быть любое скалярное поле, обозначенное любой буквой, например— обозначения градиента поляV.

Определение

Для случая трёхмерного пространства градиентом скалярной функции координат,,называется векторная функция с компонентами

, ,.

Или, использовав для единичных векторов по осям прямоугольных декартовых координат :

Если — функцияпеременных, то её градиентом называется-мерный вектор

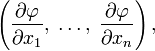
компоненты которого равны частным производным по всем её аргументам.

Размерность вектора градиента определяется, таким образом, размерностью пространства (или многообразия), на котором задано скалярное поле, о градиенте которого идет речь.

Оператором градиента (обозначаемым обычно, как говорилось выше, или) называется оператор, действие которого на скалярную функцию (поле) дает ее градиент. Этот оператор иногда коротко называют просто "градиентом".

Смысл градиента любой скалярной функции в том, что его скалярное произведение с бесконечно малым вектором перемещениядаетполный дифференциал этой функции при соответствующем изменении координат в пространстве, на котором определена , то есть линейную (в случае общего положения она же главная) часть измененияпри смещении на. Применяя одну и ту же букву для обозначения функции от вектора и соответствующей функции от его координат, можно написать:

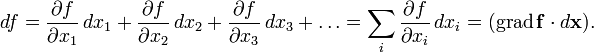
Стоит здесь заметить, что поскольку формула полного дифференциала не зависит от вида координат , то есть от природы параметров x вообще, то полученный дифференциал является инвариантом, то есть скаляром, при любых преобразованиях координат, а поскольку— это вектор, то градиент, вычисленный обычным образом, оказываетсяковариантным вектором, то есть вектором, представленным в дуальном базисе, какой только и может дать скаляр при простом суммировании произведений координат обычного (контравариантного), то есть вектором, записанным в обычном базисе. Таким образом, выражение (вообще говоря — для произвольных криволинейных координат) может быть вполне правильно и инвариантно записано как:

или, опуская по правилу Эйнштейна знак суммы,

(в ортонормированном базисе мы можем писать все индексы нижними, как мы и делали выше). Однако градиент оказывается настоящим ковариантным вектором в любых криволинейных координатах.

Пример

Например, градиент функции будет представлять собой:

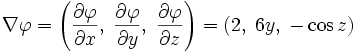
В физике

В различных отраслях физики используется понятие градиента различных физических полей.

Например, напряженность электростатического поля есть минус градиент электрического потенциала, напряженность гравитационного поля (ускорение свободного падения) в классической теории гравитации есть минус градиент гравитационного потенциала. Сила в классической механике есть минус градиент потенциальной энергии.

18) Найдем потенциальную энергию упругодеформированного тела (пружины). Сила упругости пропорциональна испытываемой телом деформации: где Fx_upr - проекция силы упругости на ось x; k - коэффициент упругости (для пружины - жесткость), а знак минус указывает, что Fx_upr направлена в сторону, противоположную деформации x. По третьему закону Ньютона, деформирующая сила равна по модулю силе упругости и противоположна ей по направлению:Элементарная работа dA, совершаемая силой Fx при бесконечно малой деформации dx, равнаа полная работатратится на увеличение потенциальной энергии пружины. Значит, потенциальная энергия упругодеформированного телаПотенциальная энергия системы является функцией состояния системы. Она зависит только от конфигурации системы и ее положения по отношению к внешним телам. Полная механическая энергия системы - энергия механического движения и взаимодействия:т. е. равна сумме кинетической и потенциальной энергий.

19) Сумма кинетической и потенциальной энергии тел называется полной механической энергией.

   Для полной механической энергии закон сохранения энергии имеет следующее выражение: полная механическая энергия замкнутой системы тел, взаимодействующих силами тяготения и упругости, остается неизменной.

   Основное содержание закона сохранения энергии заключается не только в установлении факта сохранения полной механической энергии, но и в установлении возможности взаимных превращений кинетической и потенциальной энергии тел в равной количественной мере при взаимодействии тел.

   Закон сохранения энергии раскрывает физический смысл понятия работы.

   Работа сил тяготения и сил упругости, с одной стороны, равна увеличению кинетической энергии, а с другой стороны, — уменьшению потенциальной энергии тел.

   Следовательно, работа равна энергии, превратившейся из одного вида в другой.

   Закон сохранения полной механической энергии в процессах с участием сил упругости и гравитационных сил является одним из основных законов механики. Знание этого закона упрощает решение многих задач, имеющих большое значение в практической жизни.

Механическая энергия консервативной системы сохраняется постоянной в процессе движения системы. E=k+п=constant

Этот закон справедлив как для замкнутых, так и для незамкнутых консервативных систем.

20) Потенциальная энергия гравитационного взаимодействия системы двух материальных точек с массами m и M, находящихся на расстоянии  R одна от другой, равна

где G – гравитационная постоянная, а нуль отсчета потенциальной энергии (Е_p = 0) принят при r = ∞.

G — гравитационная постоянная, равна примерно 6,6725×10-11 м³/(кг·с²).

20. Энергия гравитационного взаимодействия для двух тел.

Гравитационная энергия — потенциальная энергия системы тел (частиц), обусловленная их взаимным тяготением.

Гравитационно-связанная система — система, в которой гравитационная энергия больше суммы всех остальных видов энергий (помимо энергии покоя).

Общепринята шкала, согласно которой для любой системы тел, находящихся на конечных расстояниях, гравитационная энергия отрицательна, а для бесконечно удалённых, то есть для гравитационно не взаимодействующих тел, гравитационная энергия равна нулю. Полная энергия системы, равная сумме гравитационной и кинетической энергии, постоянна. Для изолированной системы гравитационная энергия является энергией связи. Системы с положительной полной энергией не могут быть стационарными.

Для двух тяготеющих точечных тел с массами M и m гравитационная энергия равна:

,