
- •17. Теорема Вариньона
- •19. Опорные устройства балочных систем
- •20.Проекция силы на ось и на плоскость
- •22.Связи и их реакции. Аксиома связей
- •24. Равнодействующая сходящихся сил и условие их равновесия
- •25. Мощность и кпд
- •27.Скорость
- •33. Силы инерции твердого тела
- •34. Понятие о плоскопараллельном движении твердого тела
- •35. Силы инерции при прямолинейном и криволинейном движении материальной точки
- •36. Теоремы о сложении скоростей и ускорений точки при сложном движении
- •37.Принцип Даламбера
Пара сил. Момент пары. Доказать теорему о моментах сил пары. Момент относительно оси.
Парой сил называется система двух равных по модулю, параллельных и направленных в противоположные стороны сил, действующих на абсолютно твердое тело. Система сил F, F’ образующих пару, очевидно, не находится в равновесии (эти силы не направлены вдоль одной прямой). В то же время пара сил не имеет равнодействующей, поскольку, как будет доказано, равнодействующая любой системы сил равна_ее главному вектору R, т. е. сумме этих сил, а для пары R=F+F'= 0.
Плоскость, проходящая через линии действия пары сил, называется плоскостью действия пары. Расстояние d между линиями действия сил пары называется плечом пары. Действие пары сил на твердое тело сводится к некоторому вращательному эффекту, который характеризуется величиной, называемой моментом пары. Этот момент определяется:
1) его модулем, равным произведению Fd
2) положением в пространстве плоскости действия пары;
3) направлением поворота пары в этой плоскости.
Таким образом, как и момент силы относительно центра, это величина векторная.
Моментом пары сил называется вектор М, модуль которого равен произведению модуля одной из сил пары на ее плечо и который направлен перпендикулярно плоскости действия пары в ту сторону, откуда пара видна стремящейся повернуть тело против хода часовой стрелки
Заметим еще, что так как плечо силы F относительно точки А равно d, а плоскость, проходящая через точку А и силу F, совпадает с плоскостью действия пары, то одновременно т=тА (F)=AB*F. Но в отличие от момента силы вектор т, может быть приложен в любой точке (такой вектор называется свободным). Измеряется момент пары, как и момент силы, в ньютон- метрах.
Моменту пары можно дать другое выражение: момент пары равен сумме моментов относительно любого центра О сил, образующих пару, т. е.
m=mo(F)+m0(F').

Для доказательства проведем из произвольной точки О (рис. 33) радиусы-векторы rА=ОА и rв=ОВ. Тогда согласно формуле m=mo(F)+m0(F')
Учтя еще что F’=-F, получим
m0(F)=rB*F, т0(F’) =rA*F' =-rA*F и, следовательно,
m0 (F) + m0 (F’) = (RВ—RA) *F=AB*F.
Так как AB*F=m, то справедливость равенства доказана.
момент пары равен моменту одной из ее сил относительно точки приложения другой силы. Отметим еще, что модуль момента пары
m-=Fd. (151
Если принять, что действие пары сил на твердое тело (ее вращательный эффект) полностью определяется значением суммы моментов сил пары относительно любого центра О - две пары сил, имеющие одинаковые моменты, эквивалентны, т. е. оказывают на тело одинаковое механическое действие.
Момент силы относительно центра или точки. Перечислить отчего зависит вращательный эффект силы. Записать основные свойства момента силы.
Момент силы относительно центра. Когда все силы системы лежат в одной плоскости, их моменты относительно любого центра О, находящегося в той же плоскости, перпендикулярны этой плоскости, т. е. направлены вдоль одной и той же прямой. Тогда, не прибегая к векторной символике, можно направления этих моментов отличить одно от другого знаком и рассматривать момент силы F относительно центра О как алгебраическую величину. Условимся для краткости такой момент называть алгебраическим и обозначать символом m0(F). Алгебраический момент силы F относительно центра О равен взятому с соответствующим знаком произведению модуля силы на ее плечо, т. е.*
m0(F)=±Fh.
При этом в правой системе координат, принятой в механике, момент считается положительным, когда сила стремится повернуть
Вращательный эффект действия силы на тело относительно оси определяется моментом силы относительно оси. Момент силы относительно оси находится иначе, чем момент силы относительно точки.
Алгебраический момент силы относительно некоторой оси равен алгебраическому моменту проекции силы на плоскость, перпендикулярную оси, относительно точки пересечения плоскости с осью (рис. 3.2).
Правило нахождения момента относительно оси:
Необходимо спроецировать силу F на плоскость а перпендикулярную оси z.
Подсчитать момент проекции силы fa относительно точки пересечения оси с плоскостью
M(F) = ±F,h. (3.2)
Момент силы относительно оси считается положительным, если при взгляде с положительного направления оси проекция силы Ра стремится повернуть тело против часовой стрелки.
Сила, параллельная оси, и сила пересекающая ось, не создают вращения относительно этой оси, то есть моменты таких сил относительно оси равны нулю.
Свойства момента сил
1) момент силы не изменяется при переносе точки приложения силы вдоль ее линии действия;
2) момент силы относит. точки =0 только тогда, когда сила =0 или когда линия действия силы проходит через точку (т.е. плечо =0). Если x,y,z — координаты точки приложения силы, Fx, Fy, Fz — проекции силы на оси координат и точка 0 — начало координат, то
=(yFz — zFy)+(zFx — xFz)+(xFy — yFx), откуда проекции момента силы на оси коорд.: М0x()=yFz — zFy; М0y()=zFx — xFz; М0z()=xFy — yFx.
Сложение и разложение двух параллельных сил, расположенных в одну сторону
Пусть параллельные и одинаково направленные силы F1 и F2 приложены к точкам А и В тела и нужно найти их равнодействующую (рис. 3.1). Приложим к точкам А и В равные по модулю и противоположно направленные силы Q1 и Q2 (их модуль может быть любым); такое добавление можно делать на основании аксиомы 2. Тогда в точках А и В мы получим две силы R1 и R2: R1~(F1, Q1) и R2~(F2, Q2). Линии действия этих сил пересекаются в некоторой точке О. Перенесем силы R1 и R2 в точку О и разложим каждую на составляющие: R1~(F1’, Q2’) и R2~(F2’, Q2’). Из построения видно, что Q1’=Q1 и Q2’=Q2, следовательно, Q1’= –Q2’и две эти силы согласно аксиоме 2 можно отбросить. Кроме того, F1’=F1, F2’=F2. Силы F1’ и F2’ действуют по одной прямой, и их можно заменить одной силой R = F1 + F2, которая и будет искомой равнодействующей. Модуль равнодействующей равен R = F1 + F2. Линия действия равнодействующей параллельна линиям действия F1 и F2. Из подобия треугольников Оас1 и ОАС, а, также Оbс2 и ОВС получим соотношение: F1/F2=BC/AC. Этим соотношением определяется точка приложения равнодействующей R. Система двух параллельных сил, направленных в одну сторону, имеет равнодействующую, параллельную этим силам, причем ее модуль равен сумме модулей этих сил.
Условие равновесия плоской системы сходящихся сил
для равновесия тела, находящегося под действием системы сходящихся сил, необходимо и достаточно, чтобы их равнодействующая равнялась нулю: R = 0. Следовательно, в силовом многоугольнике уравновешенной системы сходящихся сил конец последней силы должен совпадать с началом первой силы; в этом случае говорят, что силовой многоугольник замкнут (рис. 2.3). Это условие используется при графическом решении задач для плоских систем силдля равновесия сходящейся системы сил необходимо и достаточно равенства нулю алгебраических сумм проекций всех сил данной системы на каждую из координатных осей. Для плоской системы сил пропадает условие, связанное с осью Z. Условия равновесия позволяют проконтролировать, находится ли в равновесии заданная система сил.
17. Теорема Вариньона
Теорема
Вариньона.
Если
рассматриваемая плоская система сил
приводится к равнодействующей, то момент
этой равнодействующей относительно
какой-либо точки равен алгебраической
сумме моментов всех сил данной системы
относительно той же самой точки.
Предположим, что система сил приводится
к равнодействующей R, проходящей через
точку О. Возьмем теперь в качестве центра
приведения другую точку O1.
Главный момент (5.5) относительно этой
точки равен сумме моментов всех сил в
общем виде: MO1=ƩMo1(Fk).
В нашем случае, имеем MO1=MOl(R),
так как главный момент для центра
приведения О равен нулю (MO=0).
Сравнивая соотношения , получаем
MO1(R)=ƩMOl(Fk);
ч.т.д. 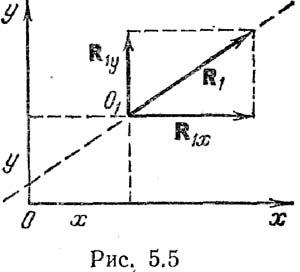
18.Аналитический
способ задания силы Выберем
систему координат Oxyz. Вектор
![]() можно
построить, зная модуль
можно
построить, зная модуль![]() и
углы
и
углы![]() между
вектором и соответствующими осями
Задание этих величин и определяет силу
между
вектором и соответствующими осями
Задание этих величин и определяет силу![]() .
Точка приложения силы должна быть задана
дополнительно координатами х, у, z. Кроме
того, силу можно задавать проекциями
на оси
.
Точка приложения силы должна быть задана
дополнительно координатами х, у, z. Кроме
того, силу можно задавать проекциями
на оси![]() .
Тогда
.
Тогда
Эти
формулы позволяют, зная проекции силы
на оси координат найти ее модуль и углы
с осями, т.е. определить силу. Зная
проекции, можно построить вектор
геометрически.
Для
плоскости формулы (2.2.1) и (2.2.2) запишутся
Построение в плоскости производится
по 4-й аксиоме статики.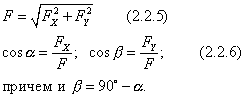
19. Опорные устройства балочных систем
Применяются следующие виды опор:
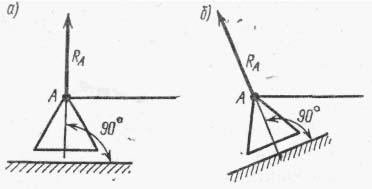
Шарнирно - подвижная опора
Здесь остается неизвестным числовое значение опорной реакции RA. Следует отметить, что опорная поверхность шарнирно-подвижной опоры может быть непараллельна оси балки (рис.б). Реакция RA в этом случае не будет перпендикулярна оси балки, так как она перпендикулярна опорной поверхности.
Шарнирно
- неподвижная опора
Эта опора допускает поворот вокруг оси шарнира, но не допускает никаких линейных перемещений. В данном случае известна только точка приложения опорной реакции — центр шарнира; направлениеи значение опорной реакции неизвестны. Обычно вместо определения значения и направления (полной)реакции RA находят ее составляющие RAx и RAy.
Жесткая
заделка (защемление)Такая опора не
допускает ни линейных перемещений, ни
поворота.Неизвестными в данном случае
являются не только значение и направление
реакции, но и точка ее приложения. Поэтому
жесткую заделку заменяют силой реакции
RA
и парой сил с моментом MA.
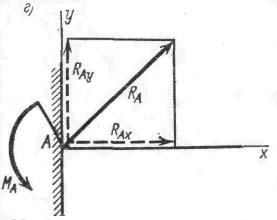
Для определения опорной реакции следует найти три неизвестных: составляющие RAx и RAy опорной реакции по осям координат и реактивный момент MA.
20.Проекция силы на ось и на плоскость
Скалярная величина, равная взятой с соответствующим знаком длине отрезка, заключенного между проекциями начала и конца силы называется проекцией силы на ось.
Знак плюс проекция имеет, если перемещение от начала к концу происходит в положительном направлении оси, и знак минус если в отрицательном.
Таким образом, проекции данной силы на любые параллельные и одинаково направленные оси равны друг другу.
Проекция
силы
![]() на
ось Ох обозначается как
на
ось Ох обозначается как![]() To
есть проекция силы на ось равна
произведению модуля силы на косинус
угла между направлением силы и
положительным направлением оси.
To
есть проекция силы на ось равна
произведению модуля силы на косинус
угла между направлением силы и
положительным направлением оси.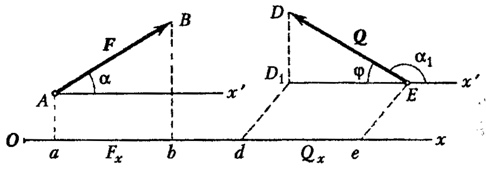
Если
сила перпендикулярна оси, то ее проекция
на эту ось равна нулю.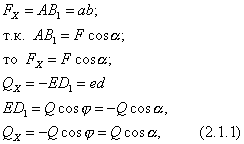
Проекцией
силы
![]() на
плоскость Оху называется вектор
на
плоскость Оху называется вектор![]() ,
заключенный между проекциями начала и
конца силы F на эту плоскость (рис. 13
,
заключенный между проекциями начала и
конца силы F на эту плоскость (рис. 13![]() ).
).
Проекция
силы на плоскость есть величина векторная
и характеризуется как модулем, так и
направлением в плоскости Оху. Модуль
проекции силы
![]() на
плоскость Оху выражается как
на
плоскость Оху выражается как![]() Тогда проекции на оси Ох и Оу:
Тогда проекции на оси Ох и Оу:![]()
21. разложение сил. Разложить данную силу на несколько составляющих — значит найти такую систему нескольких сил, для которой данная сила является равнодействующей. Эта задача является неопределенной и имеет однозначное решение лишь при задании дополнительных условий. Рассмотрим два частных случая:
а) разложение силы по двум заданным направлениям. Задача сводится к построению такого параллелограмма, у которого разлагаемая сила является диагональю, а стороны параллельны заданным направлениям
б)разложение силы по трем заданным направлениям. Если заданные направления не лежат в одной плоскости, то задача"является определенной и сводится к построению такого параллелепипеда, у которого диагональ изображает заданную силу R, а ребра параллельны заданным направлениям. Способом разложения можно в простейших случаях пользоваться для определения сил давления на связи. Для этого действующую на тело (конструкцию) заданную силу надо разложить по направлениям реакции связей, так как согласно закону о действии и противодействии сила давления на связь и реакция связи направлены вдоль одной и той же прямой.
