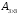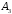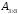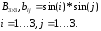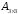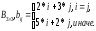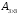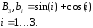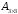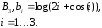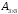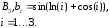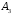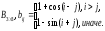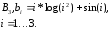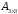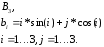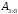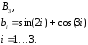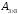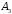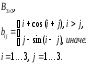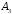Оператор цикла for

Часто при организации цикла требуется перебирать значение счетчика в заданном диапазоне значений и с заданным шагом изменения. Например, чтобы перебрать элементы вектора (массива), нужно организовать счетчик от 1 до N с шагом 1, где N – число элементов вектора. Чтобы вычислить сумму ряда, также задается счетчик от a до b с требуемым шагом изменения step. И так далее. В связи с тем, что подобные задачи часто встречаются в практике программирования, для их реализации был предложен свой оператор цикла for, который позволяет проще и нагляднее реализовывать цикл со счетчиком.

Синтаксис оператора цикла for имеет следующий вид:

for <счетчик> = <начальное значение>:<шаг>:<конечное значение>       <операторы цикла> end

Рассмотрим работу данного цикла на примере реализации алгоритма поиска максимального значения элемента в векторе:

function search_max a = [3 6 5 3 6 9 5 3 1 0]; m = a(1);                    % текущее максимальное значение for i=1:length(a)            % цикл от 1 до конца вектора а с                              % шагом 1 (по умолчанию)     if m < a(i)                   % если a(i) > m,          m = a(i);           % то m = a(i)     end end                          % конец цикла for disp(m);

В данном примере цикл for задает счетчик i и меняет его значение от 1 до 10 с шагом 1. Обратите внимание, что если величина шага не указывается явно, то он берется по умолчанию равным 1.

В следующем примере рассмотрим реализацию алгоритма смещения элементов вектора вправо, т.е. предпоследний элемент ставится на место последнего, следующий  – на место предпоследнего, и т.д. до первого элемента:

function queue a = [3 6 5 3 6 9 5 3 1 0]; disp(a); for i=length(a):-1:2              % цикл от 10 до 2 с шагом -1      a(i)=a(i-1);            % смещаем элементы вектора а end                          % конец цикла for disp(a);

Результат работы программы

3 6 5 3 6 9 5 3 1 0 3 3 6 5 3 6 9 5 3 1

Приведенный пример показывает, что для реализации цикла со счетчиком от большего значения к меньшему, нужно явно указывать шаг, в данном случае, -1. Если этого не сделать, то цикл сразу завершит свою работу и программа  будет работать некорректно.

В заключении рассмотрим работу оператора цикла for на примере моделирования случайной последовательности с законом изменения

,

где - коэффициент от -1 до 1;- нормальная случайная величина с нулевым математическим ожиданием и дисперсией

,

где - дисперсия моделируемого случайного процесса. При этом первый отсчетмоделируется как нормальная случайная величина с нулевым математическим ожиданием и дисперсией. Программа моделирования имеет следующий вид:

function modeling_x r = 0.95;                    % коэффициент модели N = 100;                     % число моделируемых точек ex = 100;                    % дисперсия процесса et = ex*(1-r^2);             % дисперсия случайной добавки x = zeros(N,1);                   % инициализация вектора х x(1) = sqrt(ex)*randn;       % моделирование 1-го отсчета for i=2:N                    % цикл от 2 до N      x(i)=r*x(i-1)+sqrt(et)*randn;          % моделирование СП end                          % конец цикла plot(x);                     % отображение СП в виде графика

При выполнении данной программы будет показана реализация смоделированной случайной последовательности .

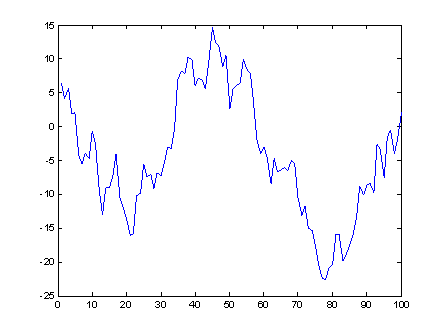
Рис. 2. Результат моделирования случайной последовательности.

Работа программы начинается с определения переменных ,(в программе переменная ex) идля реализации указанной модели. Затем вычисляется дисперсияи моделируется первый отсчет случайного процесса с помощью функции randn. Функция randn выполняет генерацию нормальных случайных величин с нулевым средним и единичной дисперсией. Чтобы сгенерировать случайную величину с дисперсиейдостаточно случайную величину с единичной дисперсией умножить на, т.к. дисперсия – это средний квадрат случайной величины относительно математического ожидания. В результате имеем программную строчку

x(1) = sqrt(ex)*randn;

Затем, реализуется цикл for со счетчиком i от 2 до N с шагом 1. Внутри цикла выполняется моделирование оставшихся N-1 отсчетов случайного процесса в соответствии с приведенной выше формулой. В последней строчке программы записана функция plot(), которая выводит смоделированную последовательность на экран в виде графика.

Задание для лабораторной работы №6

Написать файл-функцию с использованием операторов ветвления и циклов, на основании вариантов задания, представленных в таблице 1.

Таблица 1. Варианты заданий

№	Вход.массив	Формируемый массив		Задача
1	2	3		4
1				Сформировать массив А1 из минимальных элементов строк матрицы А и массив В1 из минимальных элементов строк матрицы В. Среди элементов А1 и В1 найти максимальный
2				Сформировать массив С – сумму элементов массивов А и В. Найти максимальное значение массивов А, В, С.
3				Определить минимальные элементы в матрицах А и В (mА и mВ). Вычислить С=А*В*mА*mВ.
4				Сформировать массив А1 из максимальных элементов строк матрицы А и массив В1 из максимальных элементов строк матрицы В. Упорядочить массив А1 по возрастанию, а массив В1 – по убыванию.
5				Определить максимальные элементы в матрице А и массиве В (mА и mВ). Вычислить С=А*В*mА*mВ.
6				Сформировать массив А1 из средних значений элементов строк матрицы А. Упорядочить массив А1 по возрастанию, а В – по убыванию. Осуществить поэлементное умножение А1 и В.
7				Заменить строку матрицы А, содержащую максимальный элемент, массивом В. Вычислить сумму элементов полученной матрицы.
8				Массив А упорядочить по возрастанию и заменить им последнюю строку матрицы В.
9				Упорядочить по возрастанию массивы А и В. Осуществить поэлементное деление упорядоченных массивов. Определить произведение элементов результирующего массива.
10				Вычислить произведение элементов матрицы А (рА) и сумму элементов матрицы В (сВ). Вычислить матрицу С=рА*сВ*А*В'.
11				Определить минимальные элементы в матрицах А и В (mА и mВ). Вычислить С=А*В*mА*mВ.
12				Сформировать массив А1 из максимальных элементов строк матрицы А. Осуществить поэлементное умножение А1*В. Упорядочить массив А1 по возрастанию.
13				Заменить строку матрицы А, содержащую минимальный элемент, массивом В. Вычислить произведение элементов полученной матрицы.
14			Массив А упорядочить по убыванию и заменить им первую строку матрицы В.
15			Сформировать массив С – произведение элементов массивов А и В. Найти максимальные и минимальные значения массивов А, В, С.

Содержание отчета

1. Цель работы.

2. Описание операторов, используемых для выполнения задания.

3. Листинг файла-сценария и результаты работы программы.

4. Ответы на контрольные вопросы.

Контрольные вопросы

1. Какое значение имеют файлы с расширениями .mat и .m?

2. Как можно вызвать многооконный редактор–отладчик?

3. М–файлы каких типов можно создать в редакторе-отладчике?

4. Структура и свойства М-файла-сценария.

5. Структура и свойства М-файла-функции.

6. Какие операторы используются для организации диалогового ввода и вывода?

7. Какие операторы служат для организации ветвлений. Конструкции условных операторов и оператора выбора.

8. Какие операторы сравнения могут применяться в системе MATLAB?

9. Какие логические операции применяются в системе MATLAB? В виде каких функций их можно записывать?

10. Какие операторы служат для организации циклов. Конструкции циклических операторов.