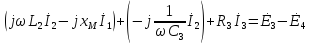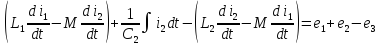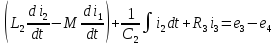ТОЭ РГР, вариант 19
.docxФедеральное государственное автономное образовательное учреждение
высшего профессионального образования
«СИБИРСКИЙ ФЕДЕРАЛЬНЫЙ УНИВЕРСИТЕТ»
ПОЛИТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ
Кафедра «Электротехнология и электротехника»
Расчетно-графическая работа № 2
ЭЛЕКТРИЧЕСКИЕ ЦЕПИ СИНУСОИДАЛЬНОГО ТОКА
Студент ФЭ12-06Б А.А.Никитин
Преподаватель Ю.С. Перфильев
Красноярск 2013
Задание
Вариант 19
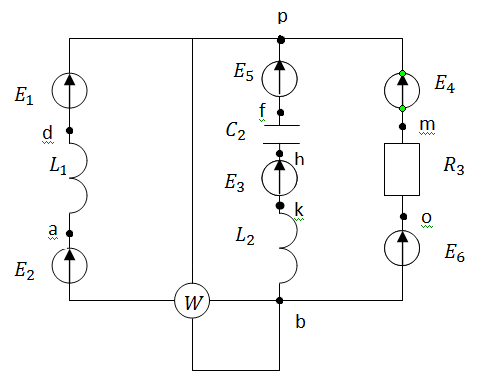
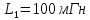
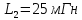
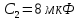
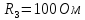
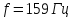
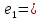 169sin(ωt+
169sin(ωt+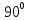 )В
)В
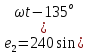 В
В
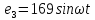
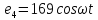
Рис.1 Исходная схема
-
На основании законов Кирхгофа составить в общем виде систему уравнений для расчета токов во всех ветвях, записав её в двух формах:
-
дифференциальной;
-
символической.
-
Определить комплексы действующих значений тока во всех ветвях воспользовавшись одним из методов расчета линейных электрических цепей.
-
По результатам, полученным в п.2, определить показания ваттметра двумя способами:
-
с помощью выражения для комплексов тока и напряжения на ваттметре;
-
по формуле
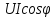 .
.
С
помощью векторной диаграммы тока и
напряжения, на которые реагируют
ваттметры, пояснить определение угла
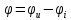 .
.
-
Построить топографическую диаграмму, совмещенную с векторной диаграммой тока. При этом потенциал точки
 ,
указанной на схеме, принять равным
нулю.
,
указанной на схеме, принять равным
нулю. -
Используя данные расчетов полученных в п.2 записать выражение для мгновенного значения тока или напряжения. Построить график зависимости указанной величины
-
Пологая, что между двумя любыми индуктивными катушками, расположенными в различных ветвях заданной схемы, имеется магнитная связь при коэффициенте взаимной индуктивности, равном М составить в общем виде систему уравнений по законам Кирхгофа для расчета токов во всех ветвях схемы записав её в двух формах:
-
дифференциальной;
-
символической.
Подготовка исходных данных
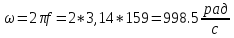
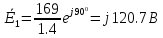
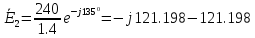 В
В
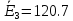 В
В
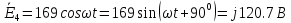
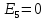
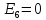
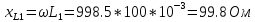

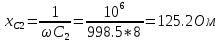
1.
На основании законов Кирхгофа составим
в общем виде систему уравнений для
расчета токов во всех ветвях

а) Дифференциальная форма:
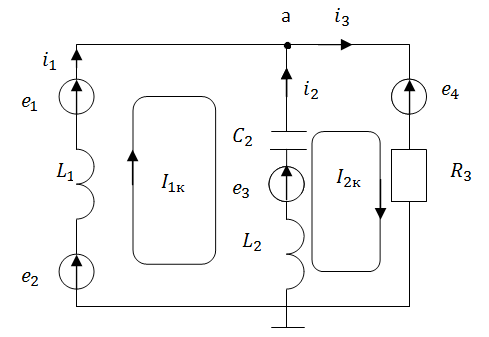
Рис.2 Схема для составления уравнений Кирхгофа
в дифференциальной форме
(а)
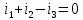
(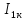 )
)
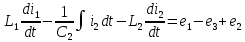
(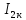 )
)
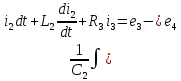
б) Символическая форма:
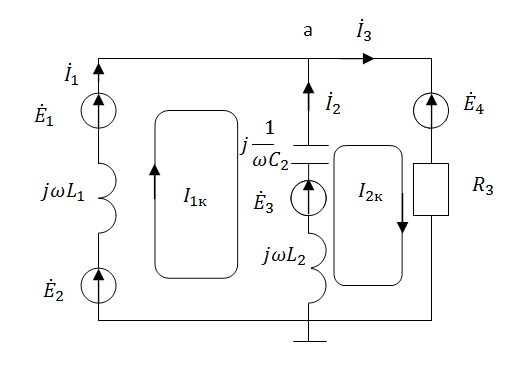
Рис.3 Схема для составления уравнений Кирхгофа
в символической форме
(а)
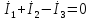
(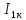 )
)
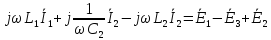
(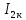 )
)
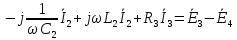
2. Определим комплексы действующих значений тока во всех ветвях, воспользовавшись методом между двумя узлами.
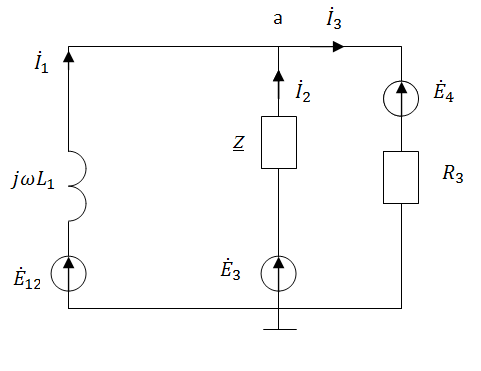
Рис.4 Схема для определения действующих значений тока в ветвях.
Т.к.
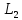 и
и
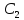 соединены последовательно, то
соединены последовательно, то
Z=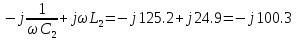
Т.к.
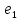 и
и
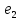 соединены последовательно, то:
соединены последовательно, то:
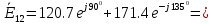 121.2
121.2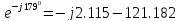
Найдём потенциал точки а:
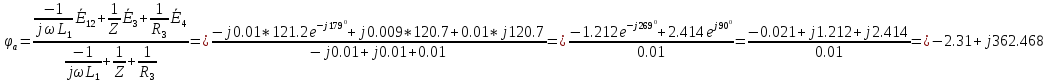
Рассчитаем токи в ветвях по обобщенному закону Ома:
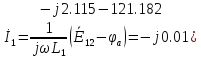 +
(
+
(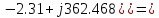
 A
A
 A
A

3. Определим показания ваттметра
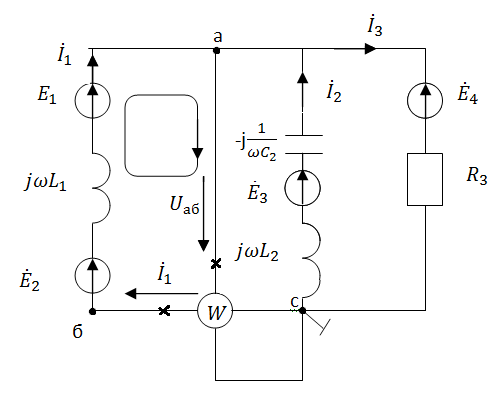
Рис.5 Схема для нахождения показаний ваттметра
Т.к.
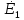 и
и
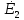 соединены последовательно, то:
соединены последовательно, то:
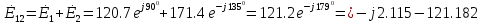
а) с помощью выражения для комплексов тока и напряжения на ваттметре;
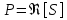
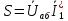
 В
В
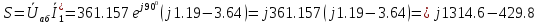
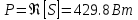
б)
по формуле
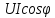 ;
;
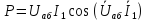
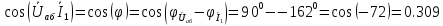
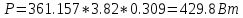
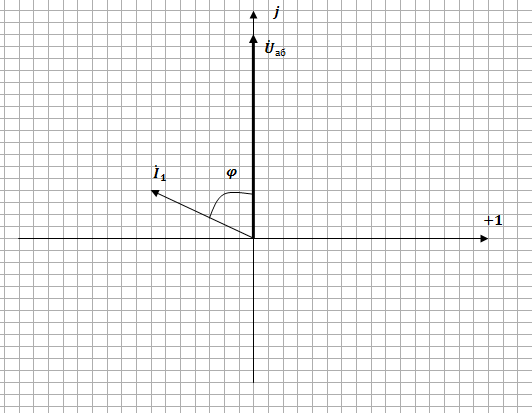
С
помощью векторной диаграммы тока и
напряжения, на которые реагируют
ваттметры, пояснить определение угла
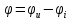 .
.
 – фазовый
сдвиг вектора тока относительно вектора
напряжения
– фазовый
сдвиг вектора тока относительно вектора
напряжения
Рис.6 Векторная диаграмма тока и напряжения действующих на ваттметр
4. Построим топографическую диаграмму, совмещенную с векторной диаграммой тока. При этом потенциал точки а примем равным нулю
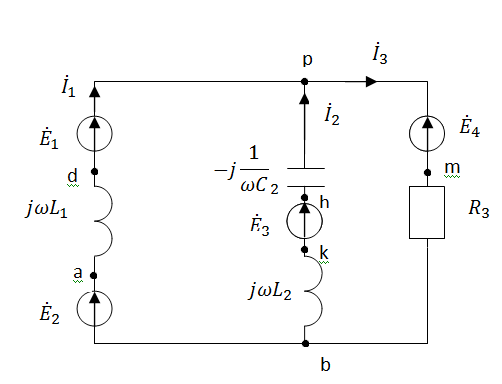
Рис.7 Схема для нахождения потенциалов точек
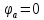
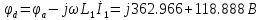
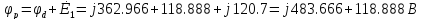
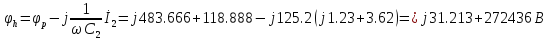
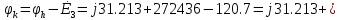
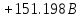
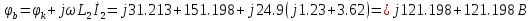
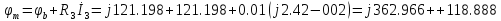 В
В
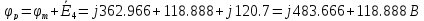
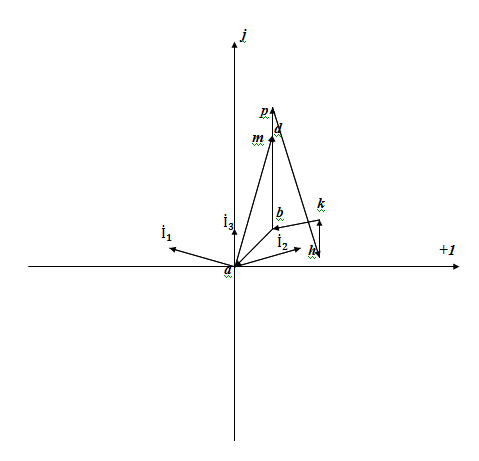
Рис.8 Топографическая диаграмма совмещенная с векторной диаграммой тока
5.
Используя данные расчетов, запишем
выражение для мгновенного значения
тока
 .
Построим график зависимости данной
величины от ωt
.
Построим график зависимости данной
величины от ωt
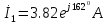
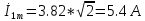
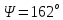
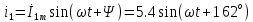 А
А
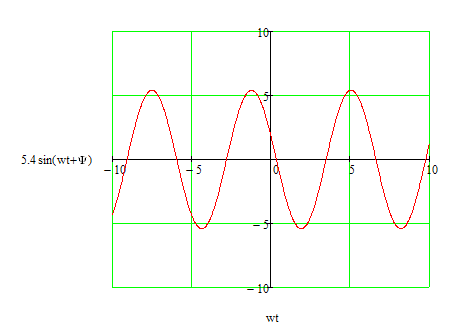
Рис.9 График мгновенного значения тока
6. Между двумя индуктивными катушками расположенных в различных ветвях заданной схемы, имеется магнитная связь при коэффициенте взаимной индуктивности, равном M, составим в общем виде систему уравнений по законам Кирхгофа для расчета токов во всех ветвях схемы
Для этого введем дополнительно вторую индуктивную катушку в первой ветви
а) Дифференциальная форма записи:
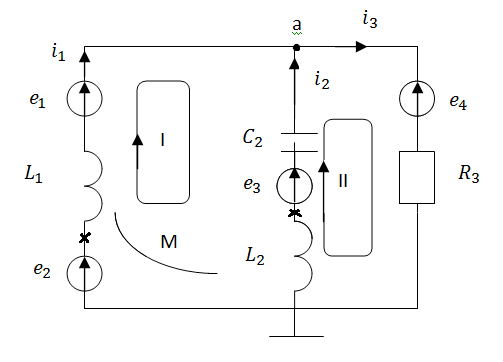
Рис. 10 Схема цепи с магнитной связью для составления
системы уравнений по законам Кирхгофа для расчета
токов в ветвях в дифференциальной форме
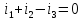 (а)
(а)
б) Символическая форма записи:
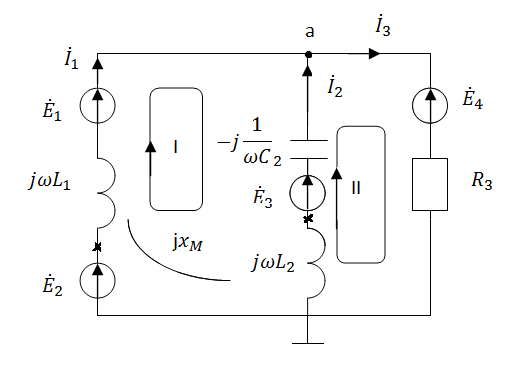
Рис. 10 Схема цепи с магнитной связью для составления
системы уравнений по законам Кирхгофа для расчета
токов в ветвях в символической форме
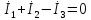 (a)
(a)
(I)
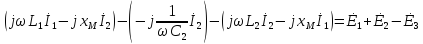
(II)