1 Анализ статической устойчивости электроэнергетической системы

Выключатели линии Q1 и Q2 и выключатель системы бесконечной мощности Q включены. Системы GS обладает бесконечным регулирующим эффектом нагрузки, что приводит к неизменности напряжения на шинах эквивалентной системы, а поэтому при изменениях режима напряжение U_н будет постоянным, рисунок 2.

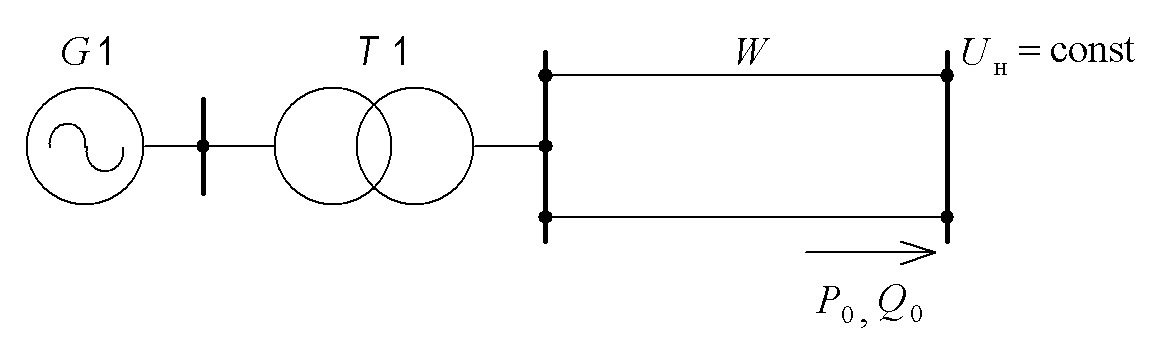
Рисунок 2 – Схема электропередачи

1. Выбор базисных условий

Расчет проводим в относительных единицах при базисных условиях и точном приведении параметров схемы к выбранной ступени напряжения, т. е. с учетом действительных коэффициентов трансформации [2].

За базисное напряжение примем напряжение на шинах эквивалентной системы GS «бесконечной» мощности U_б1 = 220 кВ. Базисную мощность примем равной S_б = 1000 МВ∙А.

Определим базисные напряжения других ступеней, кВ

2. Определение параметров режимов и схемы замещения

Определим сопротивления элементов:

– эквивалентного генератора G1

;

;

;

– эквивалентного генератора G2

;

– эквивалентного трансформатора Т1

;

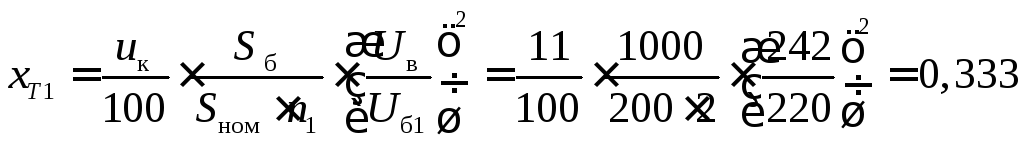– эквивалентного трансформатора Т2

;

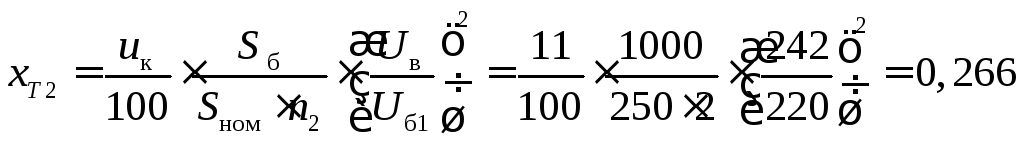– линии W:

_{Исходная схема замещения системы представлена на рисунке 3.}

Представим номинальную полную мощность нагрузки и мощность, подтекающую к шинам неизменного напряжения, в виде суммы активной и реактивной составляющих.

Мощность нагрузки

Рисунок 3 – Исходная схема замещения системы

_{Передаваемая мощность электропередачи}

_{Напряжение основной ступени}

3. Анализ устойчивости электропередачи при отсутствии АРВ без учета явнополюсности ротора эквивалентного генератора

_{Расчетная схема замещения электропередачи представлена на рисунке 4.}

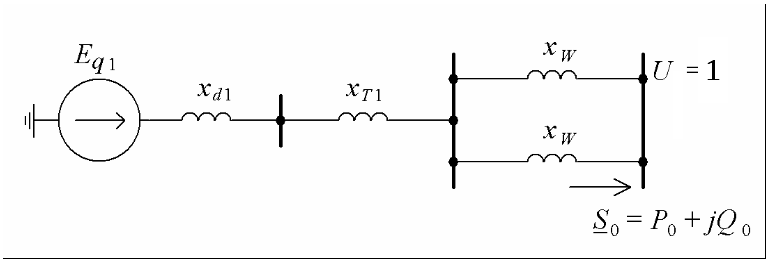
Рисунок 4 – Схема замещения электропередачи

В данном случае имеет место равенство синхронных индуктивных сопротивлений по продольной и поперечной осям x_d = x_q, а также постоянство синхронной ЭДС Е_q = const, которая пропорциональна току возбуждения i_f.

Определим сопротивление электропередачи (суммарное сопротивление электрической сети между шинами эквивалентного генератора G1 и шинами неизменного напряжения)

Суммарная реактивность

Определяем синхронную ЭДС (холостого хода) генерирующей станции

Угол сдвига векторов и

Для проверки исходного режима воспользуемся выражением, определяющим передаваемую мощность

Определим предел (идеальный) передаваемой мощности

Угловая характеристика мощности представлена на рисунке 5.

Коэффициент запаса статической устойчивости по передаваемой мощности, %

Анализируя значение коэффициента запаса статической устойчивости, можно сделать вывод о том, что система является слабо загруженной, работающей с большим запасом по статической устойчивости.

Рисунок 5 – Угловая характеристика мощности генератора G1

без учета явнополюсности и отсутствии АРВ

1.4 Анализ устойчивости электропередачи при отсутствии арв с учетом явнополюсности ротора эквивалентного генератора

Гидрогенератор представляем в расчетах синхронной реактивностью по поперечной оси x_q и фиктивной расчетной ЭДС ( зависит от режима), рисунок 6

Рисунок 6 – Схема замещения электропередачи

Суммарная реактивность

_{Расчетная ЭДС ЕQ}

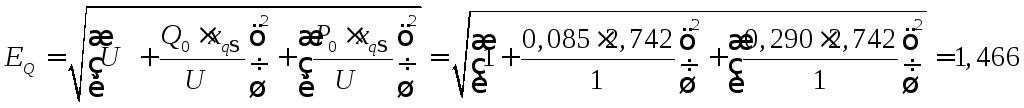
Угол сдвига векторов и

Синхронная ЭДС

Проверка исходного режима

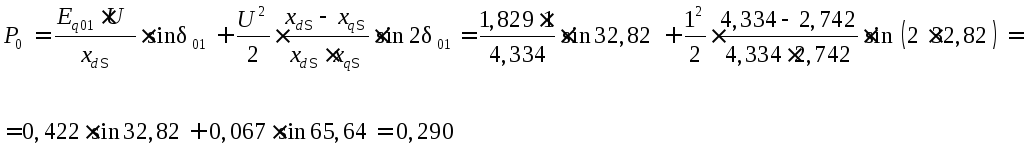
Угловая характеристика мощности представлена на рисунке 7 .

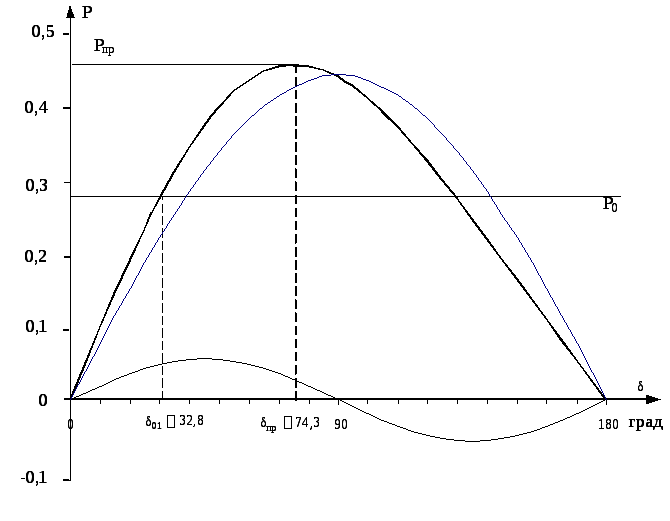
Рисунок 7 – Угловая характеристика мощности генератора G1

с учетом явнополюсности и отсутствии АРВ

Для определения предельной величины активной мощности в этом случае нужно найти угол, обеспечивающий максимальное значение последнего выражения. Приравниваем производную активной мощности по углу нулю, получим квадратное уравнение и решаем его относительно cos.

;

;

;

, ;

, не существует.

Определим предел передаваемой мощности

Коэффициент запаса статической устойчивости по передаваемой мощности, %

_{Сравнительный анализ влияния конструктивных особенностей гидрогенератора приведен в таблице 7.}

Таблица 7 – Сравнительные параметры режима генератора G1 при отсутствии АРВ с учетом и без учета явнополюсности

Параметр режима	Учет явнополюсности
	нет	да
	1,858	1,829
, град	42,5	32,82
, град	90	74,28
	0,429	0,441
, %	47,9	52,07

Учет явнополюсности увеличивает предел передаваемой мощности и, как следствие, возрастает запас статической устойчивости по передаваемой мощности. Характеристика мощности явнополюсного генератора кроме основной синусоидальной составляющей содержит вторую составляющую – синусоиду двойной частоты, амплитуда которой пропорциональна разности индуктивных сопротивлений x_d и x_q. Составляющая двойной частоты смещает максимум характеристики мощности в сторону меньших углов. Амплитуда характеристики мощности возрастет по сравнению с характеристикой, не учитывающей явнополюсности машины. У явнополюсной вращающейся машины устойчивость (по углу) нарушается раньше неявнополюсной машины равной мощности.