1.1. Простейшие способы получения цифрового сигнала

На Рис.1.3. представлен способ получения цифрового сигнала с помощью механического переключателя.

Рис.1.3. Получение цифрового сигнала при помощи механического

переключателя

Пусть механический переключатель установлен на низкий уровень (U0).

При установке механического переключателя на высокий уровень (U1) низкий уровень сразу сменяется высоким (точка A), затем из-за дребезга контактов вновь низким уровнем (точка В) и снова высоким (точка С). Хотя такое переключение происходит за короткое время, но некоторые быстродействующие электронные схемы, принимающие данный сигнал, воспринимают процесс, как чередование низкого, высокого, низкого и снова высокого уровня, что может привести к некорректной работе всей принимающей схемы.

Н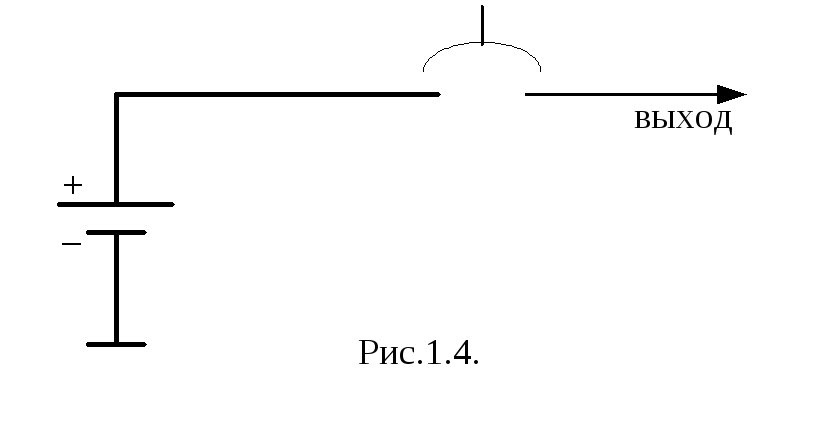а Рис.1.4. представлен способ получения цифрового сигнала с помощью кнопочного переключателя.

Если кнопка нажата, на выходе формируется высокий уровень – уровень 1.

При отпущенной кнопке уровень напряжения на выходе является неопределенным, т.к. в цепи между выходом и источником питания - разрыв.

Такая схема может быть использована при необходимости формирования только сигналов высокого уровня.

На Рис.1.5. представлен способ получения цифрового сигнала с помощью одновибратора.

При нажатии кнопки на выходе формируется короткий импульс, длительность которого не зависит от того, как долго нажата кнопка.

1.2. Простейшие способы контроля цифровых сигналов

На Рис.6.1. индикатором цифрового сигнала служит светоизлучающий диод. Резистор R ограничивает ток, проходящий через светодиод до безопасной величины.

Если переключатель в верхнем положении, то на анод светодиода подается напряжение в 5В, светодиод включен в прямом направлении, ток через него возрастает и возникает свечение.

На рисунке 1.7. представлена схема, в которой светоизлучающий индикатор управляется транзистором. Преимущество такой схемы - меньший ток, потребляемый транзистором с входа контролируемой схемы.

Если переключатель включен в верхнее положение, то на базу транзистора подается напряжение достаточное для его открытия. В цепи коллектора протекает ток, что обеспечивает индикацию сигнала высокого уровня.

1.3. Логические переменные, базовые операции между логическими переменными

Одна и та же задача может решаться аналоговыми или цифровыми методами.

Цифровые устройства, решающие задачу аналогичную с аналоговыми устройствами, содержат гораздо большее число элементов. Вместо одной линии обработки информации требуется N линий.

Цифровые устройства кажутся относительно сложными, однако они основаны на принципе многократного повторения относительно простых базовых логических схем. Связи между этими схемами строятся на основе чисто формальных методов. Даже самые сложные преобразования цифровой информации, в конечном счете, сводятся к простейшим операциям над сигналами 0 и 1.

Инструментом такого построения служит булева алгебра, которая называется также алгеброй логики.

В отличие от переменной в обычной алгебре логическая переменная в булевой алгебре имеет только два значения – "истинность" и "ложность", которые называются логическим нулем и логической единицей. В качестве обозначений используются "1" и "0".

Существуют три основные (базовые) операции между логическими переменными:

1. конъюнкция (логическое умножение), иначе операция И.

2. дизъюнкция (логическое сложение), иначе операция ИЛИ;

3. инверсия (логическое отрицание), иначе операция НЕ.

Введем условные обозначения:

• F - значение выходного сигнала:

• Х1 и Х2 - значения входных сигналов.

Тогда базовые логические операции можно записать в виде представленном в Таблице 1.1.

Таблица 1.1

Операция	Логическое выражение	Определение
Конъюнкция	F = Х1*Х2 = Х1  Х2	Значение функции И истинно (равно 1) тогда и только тогда, когда все её аргументы (Х1 и Х2) равны 1, т.е. истинны.
Дизъюнкция	F = Х1+Х2 = Х1  Х2	Значение функции ИЛИ истинно (равно 1) тогда, когда хотя бы один из ее аргументов (Х1 или Х2, или Х1 и Х2) равны 1, т.е. истинны.
Инверсия	___ F = Х1	Значение F истинно тогда, когда аргумент (Х1) является ложным

Применительно к логическим операциям существуют теоремы, приведенные в Таблице 1.2.

Таблица 1.2

Наименование	Для умножения	Для сложения
Коммутативный закон	Х1Х2 = Х2Х1	Х1+Х2 = Х2+Х1
Ассоциативный закон	Х1(Х2Х3) = (Х1Х2)Х3	Х1+(Х2+Х3) = (Х1+Х2)+Х3
Дистрибутивный закон	Х1(Х2 + Х3) = Х1Х2+ Х1Х3
Правило повторения	ХХ = Х	Х+Х=Х
Правило отрицания
Правило двойного отрицания
Теорема де Моргана:
Операции с 0 и 1:	Х1=1 Х0=0	Х+1=1 Х+0=Х

Многие из этих теорем известны из алгебры чисел. Однако некоторые теоремы для чисел несправедливы; кроме того, понятие "инверсия" (отрицание) для чисел вообще не определено.

С помощью выражений алгебры логики можно вычислить результаты логических операций для всех возможных значений входных переменных и определить их таблицы истинности.