
БНТУ / Математика / МАТЕМАТИКА ДЛЯ ИНЖЕНЕРОВ ПРИМЕРЫ И ЗАДАЧИ
.pdf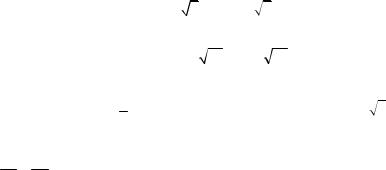
58. |
Составить уравнения асимптот гиперболы |
x2 |
− |
y2 |
=1 . |
|
|
|
|
36 |
|
|
|
|
|||||
|
|
8 |
|
x2 |
|
y2 |
|
||
59. |
Найти точки пересечения асимптот гиперболы |
|
− |
=1 с |
|||||
64 |
|
||||||||
|
|
|
|
|
36 |
|
|||
прямой 2x − y + 7 = 0 .
60.Составить уравнение гиперболы с фокусами на оси Ox , проходящей через точки (8;3
 3), (−12;6
3), (−12;6
 2 ).
2 ).
61.Составить уравнение гиперболы с фокусами на оси Ox , проходящей через точки (−9;−2
 10 ), (−6;
10 ), (−6;
 15) .
15) .
62.Составить уравнение гиперболы, если ее асимптоты заданы уравнениями y = ± 23 x и она проходит через точку (−45;10
 6 ).
6 ).
63.Найти вершины, фокусы, эксцентриситет и асимптоты гиперболы
x2 − y2 = −1.
9 16 64. Найти вершины, фокусы, эксцентриситет и асимптоты гиперболы
|
x2 |
− |
y2 |
= −1. |
|
|
|
|
|
36 |
64 |
x2 |
|
y2 |
|
||||
|
|
|
|
||||||
65. Дана |
гипербола |
− |
=1 . Найти расстояние между ее |
||||||
14 |
|
||||||||
|
|
|
|
|
25 |
|
|||
фокусами.
66.Составить уравнение параболы с вершиной в начале координат, если уравнение ее директрисы x = −5 .
67.Составить уравнение параболы с вершиной в начале координат,
симметричной относительно оси Oy и проходящей через точку
(3;−5) .
68.Составить уравнение параболы с вершиной в начале координат, симметричной относительно оси Ox и проходящей через точку пересечения прямых 2x + 3y − 5 = 0 и 3x + y − 4 = 0 .
69.Найти точку пересечения директрисы параболы y2 = 5x и прямой
4x − y +1 = 0 .
70.Найти расстояние от точки (2;−1) до фокуса параболы x2 = 24y .
201
71.Дана парабола y2 =16x . Найти длину хорды, проходящей через фокус параболы перпендикулярно ее оси.
72. Найти точки пересечения параболы x2 = 4y и прямой
2x − 5y + 33 = 0 .
73.Найти точки пересечения парабол y2 =16x и x2 =16y .
74.Найти множество середин отрезков, соединяющих точки окружности x2 + y2 − 4y − 4 = 0 и начало координат.
75. |
Найти |
точки пересечения эллипса |
|
x2 |
+ |
|
y2 |
=1 |
и гиперболы |
|||||
6 |
|
|
||||||||||||
|
|
x2 |
|
y2 |
|
8 |
|
|
|
|||||
|
|
− |
=1 . |
|
|
|
|
|
|
|
|
|
||
|
3 |
|
|
|
|
|
|
|
|
|
|
|||
|
2 |
|
|
x2 |
|
|
|
y2 |
|
|
|
|||
76. |
Найти точки пересечения гиперболы |
|
|
− |
|
=1 |
и директрисы |
|||||||
9 |
|
|
|
|||||||||||
|
|
|
|
|
|
4 |
|
|
|
|||||
параболы y2 = 24x .
77.Найти угол между фокальным радиус-вектором точки M (6;6
 2) параболы y2 =12x и биссектрисой I и III координатных четвертей.
2) параболы y2 =12x и биссектрисой I и III координатных четвертей.
78.Установить, какие кривые задают следующие уравнения. Найти их центры симметрии и полуоси:
|
а) x2 + y2 + 8x − 9 = 0 ; |
|
б) x2 − y2 + 4x −12y − 96 = 0 ; |
|
||
|
в) 2x2 + y2 + 24x − 2y − 24 = 0 ; |
г) x2 − y2 + 8x − 8y −16 = 0 ; |
|
|||
|
д) x2 + y2 − 2y − 26 = 0 ; |
|
е) 4x2 − 3y2 + 8x −12y − 26 = 0 . |
|||
79. |
Установить оси симметрии и вершины парабол: |
|
||||
|
а) x2 + y + 8x − 30 = 0 ; |
б) y2 + 6x −12y + 2 = 0 ; |
|
|||
|
в) 4y2 + 8x − 2y +10 = 0 ; г) x2 − 5x − y + 6 = 0 ; |
|
||||
|
д) x2 + 3x − 3y + 7 = 0 ; |
е) 5y2 +10y − 4x + 8 = 0 . |
|
|||
80. |
Через |
центры |
окружностей |
x2 + y2 − 4x + 6y + 9 = 0 |
и |
|
|
x2 + y2 + 8x −12y + 31 = 0 проведена прямая до пересечения |
с |
||||
осью Oy . Найти острый угол, образуемый этой прямой с положительным направлением оси Oy .
202

81. |
На эллипсе |
x2 |
+ |
y2 |
=1 найти точки, один из фокальных радиусов |
||
|
|
||||||
|
16 |
25 |
|
|
|
||
|
которых равен 3. |
|
|
|
|||
82. |
Найти уравнения |
общих |
касательных |
для окружностей |
|||
|
x2 + y2 − 8x + 2y +13 = 0 и x2 + y2 + 4x − 5 = 0 . |
|
|||||
83. |
Окружность x2 + y2 + 2x − 6y − 40 = 0 пересекает прямая |
||||||
|
3x − y +16 = 0 , |
внутренний |
отрезок которой |
служит стороной |
|||
вписанного в окружность прямоугольника. Составить уравнения сторон этого прямоугольника.
84. В окружность x2 + y2 = 9 вписан правильный треугольник, одна из вершин которого имеет координаты (−3;0) . Составить
уравнения сторон треугольника.
85. Из точки O под острым углом к горизонту брошено тело, которое описав дугу параболы, упало на землю на расстоянии 40м от точки O . Найти параметр параболической траектории, если максимальная высота, достигнутая телом, равна 25м (сопротивление воздуха в расчет не принимать).
86. Вычислить площадь квадрата, вписанного в эллипс x2 + y2 =1. 36 9
87. Определить площадь прямоугольника, вписанного в эллипс
x2 + y2 =1, две противоположные стороны которого проходят
16 12
через фокусы эллипса.
88. Найти длину общей хорды параболы 3y2 = −x и окружности x2 + y2 + 2x − 4y = 0 .
89.Написать уравнения касательных, проведенных к окружности
x2 + y2 + 4x − 25 = 0 из точки A(−5;7) .
90.Составить уравнения прямых соединяющих фокусы эллипсов
x2 |
+ |
y2 |
=1 и |
x2 |
+ |
y2 |
=1. |
25 |
|
24 |
|
||||
16 |
|
49 |
|
||||
91.Стальной трос подвешен за два конца (точки крепления расположены на одинаковой высоте), расстояние между ними равно 40 м. Величина его прогиба на расстоянии 6 м от точки крепления, считая по горизонтали, равна 18 см. Определить величину прогиба этого троса в середине между точками
203
крепления, приближенно считая, что трос имеет форму дуги параболы.
§ 6. Общее уравнение кривых второго порядка
Одной из основных задач аналитической геометрии является исследование уравнения линии второго порядка и приведение его к простейшим формам.
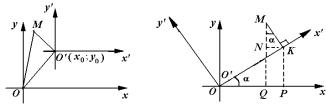
10. Преобразование прямоугольных координат. Рассмотрим три вида преобразований прямоугольных координат на плоскости:
1) параллельный перенос осей координат, когда изменяется положение начала координат, а направления осей остаются прежними
(рис. 1).
Формулы
x = x0 + x′, y = y0 + y′ . |
(1) |
устанавливают связь между старыми и новыми координатами и определяют
параллельный перенос координатных осей;
2) поворот осей координат, когда обе оси поворачиваются на один и тот же угол, а начало координат не изменяется. Формулы
x = x′cosα − y′sinα ,
(2)
y = x′sinα + y′cosα .
устанавливают связь между старыми и новыми координатами и определяют
поворот координатных осей на угол α (рис. 2);
Рис. 1 Рис. 2
3) зеркальное отображение, когда направление одной из координатных осей меняется на противоположное, а направление второй не меняется.
Формулы |
|
x = −x′, y = y′. |
(3) |
устанавливают связь между старыми и новыми координатами и определяют зеркальное отображение относительно оси Оу. Аналогичные формулы ( x = x′, y = −y′ ) получаем и при зеркальном отображении относительно
оси Ох.
20. Общее уравнение линии второго порядка. Общее уравнение линии второго порядка имеет следующий вид:
204

Ax2 + 2Bxy + Cy2 + 2Dx + 2Ey + F = 0 , |
(4) |
где A, B, C, D, E, F – любые заданные числа, но A, B и C одновременно не равны нулю (A2 + B2 + C2 ¹ 0) .
Величину AC - B2 называют инвариантом общего уравнения линии второго порядка и, в зависимости от его знака, линии второго порядка подразделяются на следующие три типа:
эллиптический, если AC - B2 > 0; гиперболический, если AC - B2 < 0 ;
параболический, если AC - B2 = 0 .
Теорема. Пусть в прямоугольной системе координат Оху задано общее уравнение линии второго порядка (4). Тогда существует такая прямоугольная система координат, в которой уравнение (4) принимает один из следующих девяти простейших (канонических) видов:
1) эллипс x2 + y2 = 1 ; a2 b2
2) мнимый эллипс x2 + y2 = -1 ; a2 b2
3) пара мнимых пересекающихся прямых a2 x2 + c2 y2 = 0 ;
4) гипербола |
x2 |
- |
y2 |
= 1 ; |
|
a2 |
b2 |
||||
|
|
|
5)пара пересекающихся прямых a2 x2 - c2 y2 = 0 ;
6)парабола x2 = 2 py ;
7)пара параллельных прямых x2 - a2 = 0 ;
8)пара мнимых параллельных прямых x2 + a2 = 0 ;
9)пара совпадающих прямых x2 = 0 .
В перечисленных х и у равноправны, т.е. их можно менять местами.
Если кривая второго порядка задана уравнением (4), то при приведении его к каноническому виду нужно последовательно поступать так:
а) |
Вычислить |
tg2α = |
2B |
. |
Затем |
cos 2α = ± |
|
1 |
, |
||||||||
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
A - C |
|
|
|
1+ tg2 2α |
|
|||
|
|
|
|
|
|
|
|
|
|
, причем знак cos 2α нужно выбрать |
|||||||
cosα = |
1 |
+ cos 2α |
|
, sinα = |
|
1- cos 2α |
|
||||||||||
|
|
2 |
|
||||||||||||||
|
|
|
|
|
2 |
A = C , |
|
|
|
|
|
||||||
таким |
же, |
как знак tg2α . |
|
Если |
то можно |
взять угол |
поворота |
||||||||||
α = 45o .
205
Применив преобразование поворота осей координат с использованием формул (2), освобождаемся в уравнении (4) от члена с произведением координат 2Bxy , т.е. получаем уравнение второй степени вида
¢ ¢ 2 |
¢ ¢ 2 |
¢ ¢ |
¢ ¢ |
+ F = 0 , |
(4’) |
A (x ) |
+ C ( y ) |
+ 2D x |
+ 2E y |
где (A¢)2 + (C¢)2 ¹ 0 .
б) Применить к уравнению (4’) параллельный перенос осей координат по формулам x′ = x0 + x′′, y′ = y0 + y′′ , где точку (x0; y0 ) найти из системы
A′x0 + D′ = 0, C′y0 + E′ = 0 . |
|
|
|
|
|
|
|
|
|
|
|||
в) Возможно |
потребуется |
|
применить |
и |
зеркальное |
отображение |
|||||||
(x′′ = -x′′′, y′′ = y′′′) . |
|
|
|
|
|
|
|
A′ |
|
|
C′ получить одно |
|
|
В зависимости |
от коэффициентов |
|
и |
из |
|||||||||
уравнений, указанных в теореме. |
|
|
|
|
|
|
|
|
|
|
|||
Пример |
1. |
Какую |
|
линию |
|
определяет |
уравнение |
||||||
6x2 +12y2 −12x − 24y +10 = 0 ? |
|
|
|
|
|
|
|
|
|
|
|||
Решение. Выделим полные квадраты для переменных x и y : |
|
||||||||||||
|
6(x2 − 2x +1)+12(y2 − 2y +1)− 8 = 0 |
|
|
||||||||||
или 3(x −1)2 + 6(y −1)2 = 4 . Разделим |
обе |
|
части уравнения на |
4. |
|||||||||
Получим уравнение эллипса |
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
(x −1)2 |
( y −1)2 |
|
|
|
||||||
|
|
|
|
|
|
+ |
|
|
|
=1 |
|
|
|
|
|
|
|
4 |
|
|
2 |
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
||
33
сцентром в точке (1;1) и полуосями a = 233 , b =  36 . □
36 . □
Пример 2. Какую линию определяет уравнение
2x2 − 9y2 + 4x + 36y − 64 = 0 ?
Решение. Выделим полные квадраты для переменных x и y : 2(x2 + 2x +1)− 9(y2 − 4y + 4)− 30 = 0
или 2(x +1)2 − 9( y −1)2 = 30 . Разделим обе части уравнения на 30. Получим уравнение гиперболы
(x +1)2 |
− |
( y − 2)2 |
=1 |
||
15 |
10 |
|
|||
|
|
|
|||
|
|
|
3 |
|
|
206

с центром в точке (−1;2) и полуосями a = |
|
b = |
|
30 |
. □ |
||||
15, |
|||||||||
|
|
||||||||
|
|
|
|
|
|
3 |
|
||
Пример 3. Привести к каноническому виду уравнения парабол |
|||||||||
а) y =10x2 - 20x + 2 ; |
б) x = y2 + 6y + 7 ; |
|
|
|
|||||
в) x = -3y2 + 2y ; |
г) y = -2x2 + 7x + 3 . |
|
|
|
|||||
Решение. |
а) |
Перепишем уравнение параболы в виде |
|||||||
y =10(x -1)2 - 8 |
или |
y + 8 =10(x -1)2 . Сделаем замену переменных |
|||||||
y′ = y + 8, x′ = x -1 . Тогда каноническое уравнение параболы имеет
вид y¢ =10(x¢)2 . В исходной системе координат получили параболу, ветви которой направлены вверх и вершина смещена в точку (1;−8) ;
б) |
Аналогично, |
перепишем уравнение в виде |
x + 2 = ( y + 3)2 . |
|||||
Сделаем |
замену |
переменных |
x′ = x + 2, y′ = y + 3 . |
Тогда |
||||
каноническое уравнение параболы имеет вид x |
¢ |
¢ |
2 |
. В исходной |
||||
|
= ( y ) |
|
||||||
системе |
координат |
ось Ox является осью |
|
симметрии |
данной |
|||
параболы. Ветви параболы направлены вправо и вершина смещена в точку (−2;−3) ;
в) Выделяя полный квадрат, получаем уравнение параболы в
|
æ |
1 |
ö2 |
|
1 |
|
|
1 |
|
æ |
1 |
ö2 |
||
виде x = -3 |
ç y - |
|
÷ |
+ |
|
|
или x - |
|
= -3 |
ç y - |
|
÷ |
. Используя замену |
|
3 |
3 |
3 |
3 |
|||||||||||
|
è |
ø |
|
|
|
è |
ø |
|
||||||
переменных y¢ = y - 13, x¢ = x - 13 , получаем каноническое уравнение
параболы x¢ = -3( y¢)2 . В исходной системе координат ось Ox является осью симметрии данной параболы. Ветви параболы
направлены влево и вершина смещена в точку æ 1 ; 1 ö ;
ç ÷ è 3 3 ø
г) Аналогично, |
|
|
|
получаем |
|
уравнение |
параболы |
||||||||||||||||||
æ |
7 ö2 |
|
|
49 |
|
|
|
|
|
|
|
|
|
|
|
73 |
æ |
|
7 |
ö2 |
|
||||
y = -2ç x - |
|
÷ |
+ |
|
+ 3 |
или |
y - |
|
|
|
= -2ç x - |
|
÷ . Сделаем замену |
||||||||||||
|
8 |
8 |
|
4 |
|||||||||||||||||||||
è |
4 ø |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
è |
|
ø |
|
||||||
|
|
|
¢ |
|
|
|
73 |
|
¢ |
|
|
|
|
7 |
|
|
|
|
|
|
|
|
|||
переменных y |
= y |
- 8 |
, x |
= x - 4 . |
Тогда |
каноническое |
уравнение |
||||||||||||||||||
|
|
||||||||||||||||||||||||
параболы имеет вид |
y |
¢ |
|
|
|
¢ |
2 |
. В исходной системе координат это |
|||||||||||||||||
|
= -2(x ) |
|
|||||||||||||||||||||||
уравнение |
параболы, |
|
ветви |
которой направлены вниз |
и вершина |
||||||||||||||||||||
207
смещена в точку çæ |
7 |
; |
73 |
÷ö . □ |
|
|
|
|
|
|
||
|
8 |
|
|
|
|
|
|
|||||
è 4 |
|
ø |
|
|
|
|
|
|
||||
Пример 4. Привести уравнения гипербол |
|
|
||||||||||
а) y = |
3x + 2 |
; |
|
б) y = |
9x + 2 |
; в) y = |
5x + 3 |
|
; г) y = |
3x |
||
|
|
6x + 7 |
2x +1 |
4x - 3 |
||||||||
|
3x - 3 |
|
|
|
|
|
||||||
к виду x′y′ = k . Записать уравнения асимптот гипербол в случаях а) и
г) в первоначальной системе координат. |
|
|
|
|
|
|
|||||
Решение. а) Выделим целую часть и получим |
|
|
|
|
|
||||||
y = |
3x + 2 |
= |
(3x - 3) + 5 |
=1+ |
5 |
|
. |
|
|
|
|
|
|
3x - 3 |
|
|
|
||||||
|
3x - 3 |
3x - 3 |
|
5 |
|
|
|||||
|
|
|
|
|
|
|
|
|
|
||
Тогда уравнение гиперболы можно записать |
y -1 = |
3 |
|
или, |
|||||||
x -1 |
|||||||||||
|
|
|
|
|
|
5 |
|
|
|||
используя замену y′ = y -1, x′ = x -1, в виде x¢y¢ = |
. Асимптотами |
||||||||||
3 |
|||||||||||
|
|
|
|
|
|
|
|
|
|
||
гиперболы в первоначальной системе координат являются прямые
x =1, y =1; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
б) Аналогично, будем иметь |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
9x + 2 |
|
|
9 |
(6x |
+ 7) - |
51 |
|
9 |
|
|
|
51 |
|
|
|
|
|
|
9 |
|
|
|
|
51 |
|
|
|
|
|
|
|
|
|||||||||||||||||
y = |
= |
|
6 |
6 |
= |
- |
|
|
6 |
|
|
|
|
= |
|
|
- |
|
|
36 |
|
|
. |
|
|
|
|
|||||||||||||||||||||||
6x + 7 |
|
|
|
|
6x + 7 |
|
|
|
6 |
6x + |
7 |
6 |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x + |
|
7 |
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6 |
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
9 |
|
|
|
|
|
|
51 |
|
|
|
|
|||||||
Тогда уравнение |
гиперболы |
|
примет |
вид |
|
y - |
= - |
|
|
36 |
|
|
или, |
|||||||||||||||||||||||||||||||||||||
|
6 |
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x + |
|
7 |
|
|
|
|
||||||||
|
|
|
|
|
|
|
9 |
|
|
|
|
|
7 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
51 |
6 |
|
|
|
|
||||||||||||
|
|
¢ |
|
|
|
|
|
¢ |
|
|
|
|
|
|
|
|
|
|
|
¢ |
|
¢ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
используя замену y |
= y - 6 , x |
= x + |
|
|
|
|
|
|
|
|
|
|
|
|
= - 36 ; |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
6 , получим x y |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
5 |
|
|
|
|
5 |
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|||||
в) Имеем |
y = |
5x + 3 |
= |
2 (2x |
+1) - |
2 |
+ |
3 |
= |
5 |
+ |
|
|
|
2 |
|
|
= |
5 |
|
+ |
4 |
|
. |
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
2x +1 |
|
|
|
|
1 |
||||||||||||||||||||||||||||||||||
|
|
|
|
2x +1 |
|
2x +1 |
|
|
|
2 |
|
|
|
2 |
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x + |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Тогда уравнение гиперболы можно записать |
|
y - |
= |
|
|
|
|
4 |
|
|
|
|
или, вводя |
|||||||||||||||||||||||||||||||||||||
|
2 |
|
x + |
1 |
|
|
||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
208
замену y′ = y − |
5 |
, x′ = x + |
1 |
, в виде x′y′ = |
1 |
; |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
г) Проводя аналогичные рассуждения будем иметь |
|
|
|
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
3x |
|
|
|
|
|
3 |
(4x − 3) + |
9 |
|
|
|
|
|
3 |
|
|
|
|
|
|
9 |
|
|
|
3 |
|
9 |
|
|
|
||||||
|
|
y = |
|
|
|
|
= |
|
4 |
4 |
|
= |
|
|
+ |
|
4 |
|
|
= |
+ |
16 |
|
|
, |
|||||||||||||||||
|
|
|
4x − 3 |
|
|
4x − 3 |
|
|
|
4x − 3 |
|
|
3 |
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
4 |
|
x − |
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
9 |
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
получаем |
уравнение |
в |
виде |
y − |
|
= |
|
16 |
|
|
|
|
или, |
используя замену |
||||||||||||||||||||||||||||
|
|
|
3 |
|
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
x − |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
3 |
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
9 |
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
y′ = y − |
, x′ = x − |
, |
в |
|
виде |
x′y′ = |
|
. Асимптотами гиперболы в |
||||||||||||||||||||||||||||||||||
|
|
|
16 |
|||||||||||||||||||||||||||||||||||||||
4 |
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
первоначальной системе координат являются прямые x = 34 , y = 34 . □
Пример 5. Установить, какие кривые определяются следующими уравнениями и построить их:
а) 47x2 +17 y2 − 94x + 34y − 7 = 0 , б) 16x2 − 7 y2 − 32x + 28y − 51 = 0 , в) x2 + 6y2 − 4x +12y +15 = 0 , г) 2x2 − 4x + 7 y −18 = 0 ,
д) y2 − 6y + 8 = 0 , е) x2 + 2x + 7 = 0 , ж) 8x2 −18xy + 8y2 + 
 2x − 5 = 0 , з) 14x2 + 24xy + 21y2 − 4x +18y −141 = 0 .
2x − 5 = 0 , з) 14x2 + 24xy + 21y2 − 4x +18y −141 = 0 .
Решение: а) выделим полные квадраты для переменных x и y :
47(x2 − 2x +1)− 47 +17(y2 + 2y +1)−17 − 7 = 0 или |
|
||||||||||||||
47(x −1)2 +17(y +1)2 = 71. Разделим |
обе |
|
части уравнения на 71 и |
||||||||||||
получим уравнение эллипса |
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
(x −1)2 |
( y +1)2 |
|
|||||||
|
|
|
|
|
|
|
|
|
|
+ |
|
|
|
=1 |
|
|
|
|
|
|
|
|
71 |
|
|
|
71 |
||||
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
47 |
|
|
|
|
17 |
|
|
|
|
с |
центром в |
точке |
(1;−1) и полуосями |
|||||||||||
|
|
|
|
|
|
|
|
|
|||||||
|
a = |
|
71 |
|
≈1,23, b = |
71 |
≈ 2,04 (рис. 3); |
||||||||
|
47 |
17 |
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||
Рис. 3 |
б) выделим полные квадраты: |
|
|||||||||||||
209

16(x2 - 2x +1)-16 - 7(y2 - 4y + 4)+ 28 - 51 = 0
или 16(x -1)2 - 7( y - 2)2 = 39 . Разделим обе части уравнения на 39 и
получим |
уравнение |
гиперболы |
(x -1)2 |
- |
(y - 2)2 |
=1 с полуосями |
||||||||||
|
39 |
|
|
39 |
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
16 |
|
|
7 |
|
|
||
a = |
|
39 |
|
»1,56, b = |
39 |
|
» 2,36 (рис. 4); |
|
|
|
|
|
||||
4 |
|
7 |
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Рис. 4 |
Рис. 5 |
Рис. 6 |
в) выделим полные квадраты: |
|
|
(x2 - 4x + 4) + 6(y2 + 2y +1) + 5 = 0 или (x - 2)2 + 6( y +1)2 = -5 .
Разделим обе части уравнения на 5 и получим уравнение
(x - 2)2 + (y +1)2 = - 1 .
5 5
6
Это уравнение не представляет ни одной точки на плоскости. Однако ввиду внешнего сходства с уравнением эллипса говорят, что оно представляет “мнимый эллипс”;
|
г) преобразуем заданное уравнение: 2(x -1)2 + 7 y - 20 = 0, или |
||||||||
y = - |
2 |
(x -1)2 + |
20 |
. Это уравнение параболы, ветви которой |
|||||
7 |
|
||||||||
|
|
7 |
|
|
20 |
|
|||
направлены вниз и вершина смещена в точку çæ1; |
÷ö (рис. 5); |
||||||||
|
|||||||||
|
|
|
|
|
|
è |
7 ø |
||
|
д) |
уравнение |
y2 - 6y + 8 = 0 или (y − 2)( y − 4) = 0 распадается |
||||||
на два: |
y = 2, y = 4 . |
Таким образом, согласно теореме 1 п.7) имеем |
|||||||
две горизонтальные прямые (рис. 6);
210
