
БНТУ / Математика / МАТЕМАТИКА ДЛЯ ИНЖЕНЕРОВ ПРИМЕРЫ И ЗАДАЧИ
.pdf
а) a = 2i + 3 j + k - 12 (2i + 8 j + 6k );
|
|
|
|
|
|
|
|
æ |
1 |
|
|
|
|
|
1 |
|
|
ö |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
б) |
a = 5i + 3 j + 2k - 3 |
ç |
|
|
i |
+ j + |
|
k ÷ |
; |
|||||||||||
3 |
6 |
|||||||||||||||||||
|
|
|
|
|
|
|
|
è |
|
|
|
|
|
ø |
|
|||||
в) a = i + 2 j + k - 15 (4i + 8 j + 3k );
г) a = -i + 8 j - 6k + 4(i - j + 2k ).
6. Найти длину и |
|
направляющие |
|
косинусы вектора |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
если |
||
d |
= 3a - 5b + c , |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
a = 4 |
|
|
|
|
|
|
|
|
|
|
|
|
+ 7 |
|
+ 3 |
|
|
|
|
|
|
|
|
, |
|
|
|
|
|
|
|
|
= |
|
|
|
|
|
|
|
+ 2 |
|
|
|
|
|
+ |
|
|
|
|
|
, c = 2 |
|
|
|
- 3 |
|
|
|
|
- |
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
k |
b |
k |
k |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
i |
j |
i |
|
|
j |
|
i |
|
j |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
7. Нормировать вектор a : |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
а) a = |
|
|
|
+ 2 |
|
|
|
|
|
|
- 2 |
|
|
|
|
|
|
; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
б) a = 4 |
|
|
|
|
|
+ 3 |
|
|
; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
k |
|
|
|
|
|
|
|
|
|
|
|
|
k |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
i |
j |
|
|
|
|
|
|
|
|
|
|
|
|
i |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
в) a = |
1 |
|
|
|
|
|
|
|
+ |
|
|
2 |
|
|
|
|
|
|
|
|
- |
|
2 |
|
|
|
|
|
|
|
|
; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
г) a = 2 |
|
|
|
|
- 3 |
|
+ 6 |
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k |
|
|
|
|
|
|
|
|
|
|
|
|
k |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
i |
|
j |
|
|
|
|
|
|
|
|
|
|
|
|
i |
j |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||
8. Найти скалярное произведение векторов a и |
|
|
: |
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
b |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
а) a = 2 |
|
|
|
|
+ 3 |
|
|
|
- |
|
|
|
|
, |
|
|
|
|
|
= |
|
|
|
+ 4 |
|
|
; |
|
|
|
|
|
|
|
|
|
|
|
|
|
б) a = |
|
|
- 3 |
|
, |
|
= 3 |
|
+ 2 |
|
+ |
|
; |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
k |
b |
k |
k |
b |
k |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
i |
j |
i |
i |
i |
j |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
в) a = |
1 |
|
|
|
|
|
|
+ |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
+ |
|
|
|
|
, |
|
|
|
|
= 2 |
|
|
|
|
|
+ 3 |
|
|
|
+ 8 |
|
|
|
|
; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k |
b |
k |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
i |
|
|
j |
i |
j |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
г) a = -2 |
|
|
|
+ |
2 |
|
|
|
|
|
|
|
|
, |
|
|
= - |
|
+ 5 |
|
+ 8 |
|
|
; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
b |
k |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
i |
|
|
|
j |
i |
j |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
д) a = -2 |
|
|
+ 3 |
|
|
|
|
|
|
- |
|
|
|
, |
|
|
|
|
= |
|
1 |
|
|
|
|
+ 2 |
|
|
- 3 |
|
|
; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
k |
b |
k |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
i |
j |
i |
|
j |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
е) a = |
5 |
|
|
|
- |
|
2 |
|
|
|
|
|
|
+ |
|
|
, |
|
|
= 6 |
|
|
|
+ 3 |
|
+ 8 |
|
; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k |
b |
k |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
i |
|
|
|
|
j |
|
i |
j |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
ж) a = 4 |
|
- |
|
, |
|
|
= - |
|
- 7 |
|
|
; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
b |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
i |
j |
i |
j |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
з) a = |
|
+ 2 |
|
- |
|
, |
|
= -4 |
|
+ 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
k |
b |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
i |
j |
i |
j |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
9. При каком значении m векторы a и |
|
|
|
|
|
перпендикулярны: |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
b |
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
101
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
а) a = 2mi |
|
+ 3 j + k , b = i + mj + 3k ; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
б) a = 3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
+ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
+ k |
b |
+ 8k ; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
i |
j |
|
|
|
|
|
|
= 3mi |
|
+ mj |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
в) a = 3 |
|
|
|
+ |
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
+ 4 |
|
|
|
|
|
|
|
|
, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
- 2 |
|
|
; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k |
b |
k |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
i |
|
|
|
mj |
|
|
= 2mi |
|
|
+ 3mj |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
г) a = |
|
|
|
|
|
|
+ 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
- 3 |
|
|
|
|
+ 2 |
|
|
|
; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
+ mk |
b |
k |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
i |
j |
|
= mi |
j |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
+ 3 |
|
|
|
|
|
|
|
|
|
+ 4 |
|
|
|
|
|
|
, |
|
|
|
= 4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
- 7 |
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k |
b |
k |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
д) a = mi |
j |
i |
+ mj |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
10 |
. Определить угол между векторами a и |
|
|
|
: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
b |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
а) a = 5 |
|
|
|
|
|
+ 6 |
|
|
|
|
, |
|
|
|
= 6 |
|
|
|
|
|
|
- 5 |
|
|
|
|
|
|
; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
б) a = 3 |
|
|
|
+ 4 |
|
|
|
|
|
, |
|
|
|
|
= 5 |
|
|
+12 |
|
|
|
; |
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
k |
b |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k |
b |
k |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
i |
|
i |
|
|
j |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
j |
i |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
в) a = |
|
|
|
|
|
- |
|
|
|
|
|
|
|
+ |
|
|
|
, |
|
|
|
= 5 |
|
|
|
|
|
+ |
|
|
|
|
+ |
|
|
|
|
; г) a = |
|
|
|
- |
|
|
+ |
|
|
, |
|
|
|
= -2 |
|
+ 2 |
|
|
- 2 |
|
; |
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
k |
b |
k |
k |
b |
k |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
i |
j |
i |
|
j |
i |
j |
i |
|
j |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
д) a = 4 |
|
|
-10 |
|
+ |
|
|
, |
|
|
|
|
|
|
=11 |
|
|
- 8 |
|
- 7 |
|
; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
k |
b |
k |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
i |
j |
i |
j |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
е) a = 2 |
|
|
- |
|
|
|
- 2 |
|
, |
|
= 2 |
|
|
+ 4 |
|
|
+ 4 |
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
k |
b |
k |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
i |
|
|
j |
i |
j |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
11 |
. Даны |
|
|
a |
|
= 3 и |
|
|
|
|
|
|
|
= 4 , |
|
|
|
|
угол между векторами |
|
a |
|
|
и |
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
b |
|
|
|
|
|
|
b |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
равен |
2π |
|
|
. Найти: а) |
|
|
|
|
|
|
a2 |
; б) (3a - 2 |
|
|
|
|
)(a + 2 |
|
|
); |
|
|
|
в) |
|
(a + |
|
)2. |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
b |
b |
|
|
|
|
b |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
12 |
. Даны три вектора: |
|
a = (1;-1;1), |
|
|
= (5;1;1) |
|
и |
c = (0;3;−2). |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
b |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Найти: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
а) |
|
a |
|
2 + |
|
c |
|
2 - (a × |
|
)×( |
|
×c ); б) (a ×c )×(a × |
|
)- |
|
a |
|
2 ×( |
|
×c ). |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
b |
b |
b |
b |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
13 |
. В плоскости Оху найти вектор |
|
, перпендикулярный |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
b |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
вектору |
|
|
|
|
|
a = (5;−3;4) |
|
|
|
|
|
|
|
|
и |
|
|
|
|
|
имеющий одинаковую |
|
с |
|
|
ним |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
длину. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
14 |
|
|
= |
|
×(a ×c ) - c ×(a × |
|
) ортогонален вектору |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
. Доказать, что вектор d |
b |
b |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
a . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
102
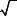
15 |
. Вычислить угол ϕ между векторами a + |
|
|
|
|
|
|
и a − |
|
, если |
||||||||||||||||||||||||||||||||||||||
b |
b |
|||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
π |
|
|
векторы |
|
|
a |
и b |
образуют |
угол, |
|
|
равный |
|
|
и |
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
6 |
|||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
= |
|
|
|
|
|
|
=1. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
3, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
b |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
16 |
. |
|
Дана |
точка |
|
|
A(3;0;5) |
и |
вектор a = |
|
|
− 9 |
|
+ 3 |
|
. |
|
|
Найти |
|||||||||||||||||||||||||||||
|
i |
j |
k |
|
|
|||||||||||||||||||||||||||||||||||||||||||
|
длину вектора |
|
|
|
|
|
, перпендикулярного вектору |
a , если |
||||||||||||||||||||||||||||||||||||||||
|
|
|
AB |
|||||||||||||||||||||||||||||||||||||||||||||
|
известно, что точка В принадлежит оси Oz. |
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||
17 |
. |
|
Найти |
|
|
внутренние |
углы |
треугольника с |
вершинами |
|||||||||||||||||||||||||||||||||||||||
|
|
A(1;7;2), B(5;−3;3), C(12;−1;−5). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
18 |
. Найти прa |
|
|
и пр |
|
a , если |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
b |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
b |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
а) |
|
a = (10;2;−11), |
|
= (−2;1;−2); |
б) |
a = (2;2;1), |
|
|
= (6;3;2); |
|
|||||||||||||||||||||||||||||||||||||
|
|
b |
b |
|
||||||||||||||||||||||||||||||||||||||||||||
|
в) |
|
a = (1;−3;1), |
|
= (12;−16;15). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
b |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
19 |
. |
|
Даны |
три вектора: |
|
a = (7;−5;3), |
|
= (−2;4;−7), с = (4;4;−2). |
||||||||||||||||||||||||||||||||||||||||
|
|
b |
||||||||||||||||||||||||||||||||||||||||||||||
|
Вычислить прc (a + |
|
) . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
b |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
20 |
. |
|
|
Даны |
|
|
две |
|
|
|
точки |
P(−5;7;6), Q(7;−9;9). |
Вычислить |
|||||||||||||||||||||||||||||||||||
|
проекцию вектора a = (1;−3;1) на вектор |
|
|
. |
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||
|
|
PQ |
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||
21 |
. |
|
|
Найти проекцию |
|
вектора |
a = (1;2;3) |
на |
ось l , |
|||||||||||||||||||||||||||||||||||||||
образующую с координатными осями равные острые углы.
22. |
|
|
Вычислить |
пр( |
|
+c )a, |
если |
||||||||
b |
|||||||||||||||
a = (4;3;8), |
|
= (4;−9;8), с = (7;1;−6). |
|
|
|
|
|||||||||
b |
|
|
|
|
|||||||||||
23. |
Представить вектор c через |
пару неколлинеарных |
|||||||||||||
векторов a, |
|
, если: |
|
|
|
|
|||||||||
b |
|
|
|
|
|||||||||||
а) |
с = (7;−5),a = (−1;3), |
|
= (1;2); |
|
|
|
|
||||||||
b |
|
|
|
|
|||||||||||
б) |
с = (−1;2),a = (−5;−1), |
|
|
|
= (−1;3); |
|
|
|
|
||||||
b |
|
|
|
|
|||||||||||
в) |
с = (2;−6),a = (−5;−1), |
|
= (−1;3). |
|
|
|
|
||||||||
b |
|
|
|
|
|||||||||||
103
24. |
Даны |
три |
вектора |
a = (3;−1), |
|
= (1;−2), с = (−1;7). |
||
b |
||||||||
Представить вектор p = a + |
|
+ c |
через пару векторов a и |
|||||
b |
||||||||
b , предварительно показав, что они неколлинеарны.
25 |
. Даны векторы |
a1 = (1;0;0), a2 = (1;1;0), a3 = (1;1;1). |
Разложить |
||
|
вектор a = (−2;0;1) |
по векторам a1, a2 , a3. |
|
||
26 |
. Даны |
три вектора |
a1 = (3;−2;1), a2 = (−1;1;2), a3 = (2;1;−3). |
||
|
Найти |
разложение |
вектора a = (11;6;−7) |
по базису |
|
a1, a2 , a3.
27. Вычислить, какую работу производит равнодействующая сил
F1 = (1;−3;4), F2 = (2;5;−5), F3 = (7;−8;9), приложенных в одной точке, когда ее точка приложения, двигаясь прямолинейно, перемещается из положения S1(3;−2;4) в положение S2 (6;8;7) .
28. |
Под действием силы |
|
|
|
|
= (5;2;1) точка перемещается из |
||||||
|
F |
|||||||||||
|
|
|
|
|
|
|
. |
|
|
|||
|
C(3;0;3) в D(−1;2;1) . Найти работу силы F |
|
|
|||||||||
29. |
Даны три силы |
|
|
|
|
|
|
|
||||
F1 = (2;4;3), F2 = (3;−2;5), F3 = (−1;3;−2), |
||||||||||||
приложенных в одной точке. Вычислить работу равнодействующей этих сил, когда ее точка приложения, двигаясь прямолинейно, перемещается из положения S1(2;−1;3) в положение S2 (7;4;8) .
30. Найти координаты вектора, совпадающего с высотой параллелограмма, построенного на векторах
a = (−1;2;−2), b = (3;5;−1), перпендикулярной к стороне a .
31. Вычислить длину диагоналей параллелограмма, построенного на
векторах |
a = 2 p − 3q и |
b |
= 3p + 4q , если известно, что |
||||||||
|
p |
|
= 2, |
|
q |
|
= 3 |
и угол между ними ϕ = |
π . |
||
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
104

32 |
. |
Даны |
вершины |
параллелограмма |
||||
|
|
A(−3;5;6), B(3;2;1), C(6;4;4) . Найти его четвертую вершину. |
||||||
33 |
. Доказать, |
что четырехугольник с вершинами A(−3;5;6), |
||||||
|
|
B(3;2;1), C(6;4;4) и |
D(4;7;−2) − квадрат. |
|
|
|||
34 |
. |
Найти |
косинус |
угла |
между |
диагоналями |
||
|
параллелограмма, |
если |
заданы три |
его вершины |
||||
|
|
A(2;1;3), B(5;2;−1), C(−3;3;−3) . |
|
|
|
|||
35 |
. |
Доказать, |
что |
cos2 α + cos2 β + cos2 γ =1, |
где |
|||
cosα,cos β ,cosγ − направляющие косинусы вектора.
36. Средствами векторной алгебры доказать, что диагонали ромба взаимно перпендикулярны.
§ 3. Векторное и смешанное произведение векторов
Тройку векторов называют упорядоченной, если указано,
какой из векторов считается первым, какой вторым и какой третьим. В записи (a;b;c ) вектор a считается первым, b – вторым, c – третьим; в записи (c;b;a) вектор c – первый, b –
второй, a – третий.
Упорядоченная тройка некомпланарных (не лежащих в одной плоскости) векторов называется правой, если после приведения их к общему началу из конца третьего вектора кратчайший поворот от первого ко второму вектору можно совершить против часовой стрелки. В противном случае указанная тройка векторов называется
левой.
10. Векторное произведение двух векторов. Векторным
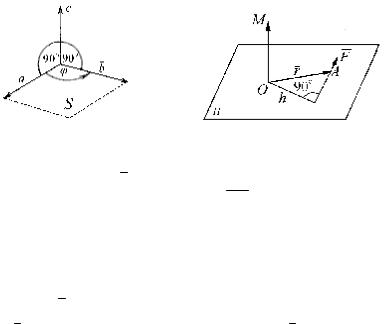
произведением векторов a и b называется вектор c , длина которого численно равна S − площади параллелограмма,
построенного на векторах a и b , приведенных к общему началу, который перпендикулярен перемножаемым векторам и
направлен так, что векторы a,b ,c образуют правую тройку векторов
(рис. 1).
Из определения векторного произведения следует, что
(рис.1)
105
|
|
c |
|
= |
|
a |
|
|
|
|
sinϕ = S , |
(1) |
|||||||||
|
|
|
|
|
b |
||||||||||||||||
где ϕ – угол между векторами a |
и |
|
, S – площадь |
||||||||||||||||||
b |
|||||||||||||||||||||
параллелограмма. |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
Векторное произведение |
двух |
векторов a и |
|
|
|||||||||||||||||
b |
|||||||||||||||||||||
обозначают символом |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
é |
|
ù |
|
|
é |
|
ù |
|
|
|||
a ´b , или |
|
|
|
|
|
|
|||||||||||||||
|
ëa b û , или |
ëa,b û . |
|||||||||||||||||||
Рис. 1 Рис. 2
Выясним физический смысл векторного произведения. В
физике момент силы F с точкой приложения А относительно точки О изображают вектором OM , перпендикулярным
плоскости, в которой |
лежат точка |
О |
и |
вектор |
|
|
(рис. 2). |
||||||||||||||||||||||
F |
|
||||||||||||||||||||||||||||
Длина |
вектора |
|
OM |
|
|
определяется |
как |
|
|
произведение |
длины |
||||||||||||||||||
вектора |
|
|
|
|
|
на |
плечо |
h , где h – расстояние от |
точки |
О до |
|||||||||||||||||||
|
|
F |
|||||||||||||||||||||||||||
прямой, на которой лежит вектор силы |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
F |
, |
т.е. |
OM |
= |
F |
× h , или |
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
OM |
= |
F |
|
r |
|
|
|
|
|
|
|
|
|
|
|
точки |
приложения |
|||||||||||
|
|
sin(F, r ), (r = OA – радиус-вектор |
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
силы F) . Таким образом, момент силы F относительно некоторой точки O , есть векторное произведение радиус-
вектора r точки приложения силы на вектор силы |
|
|
: |
||||||||||||||
F |
|||||||||||||||||
|
OM |
= |
r |
´ |
F |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
Свойства векторного произведения. |
|
|
|
||||||||||||
|
|
1) При перестановке сомножителей векторное произведение меняет знак |
|||||||||||||||
(антикоммутативность), т.е. |
|
|
|
||||||||||||||
|
|
|
|
|
|
a ´ |
|
= -( |
|
´ a) . |
(2) |
||||||
|
|
|
|
|
|
b |
b |
||||||||||
|
|
2) Ассоциативность: |
|
|
|
||||||||||||
|
|
|
|
|
|
(α a)´ |
|
= α (a ´ |
|
), α Î . |
(3) |
||||||
|
|
|
|
|
|
b |
b |
||||||||||
106
|
3) Дистрибутивность: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
(a + |
|
|
)× c = a × c + |
|
|
|
× c . |
|
|
|
|
|
|
|
|
(4) |
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
b |
b |
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||
|
4) Векторное произведение |
a × |
|
= 0 , |
|
|
если a |
и |
|
|
|
– |
коллинеарные |
|||||||||||||||||||||||||||||||||||||||||||||||
b |
|
b |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
векторы. Пусть |
векторы |
a и |
|
|
|
|
заданы своими координатами: |
|||||||||||||||||||||||||||||||||||||||||||||||||||||
b |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
a = (a1;a2;a3), |
|
|
= (b1;b2;b3 ) . |
Тогда |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
b |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
i |
|
|
|
|
j |
|
|
|
|
|
k |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a × |
|
|
= |
a1 |
|
a2 |
a3 |
. |
|
|
|
|
|
|
|
|
|
|
|
|
(5) |
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
b |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
b1 |
|
b2 |
b3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
Пример 1. Найти векторное |
|
|
произведение |
векторов |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
a = 3 |
|
+ 2 |
|
+ 7 |
|
и |
|
= 2 |
|
+ |
|
|
+ |
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
k |
b |
k |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
i |
j |
i |
j |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
Решение. |
a × |
|
= |
i |
|
|
|
|
|
|
j |
|
|
|
|
k |
|
= |
|
|
|
2 |
|
|
|
|
7 |
|
− |
|
|
3 |
7 |
|
+ |
|
|
3 |
2 |
|
= |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
b |
3 |
2 |
|
|
|
7 |
|
|
|
|
|
|
|
|
|
|
k |
|
|
||||||||||||||||||||||||||||||||||||||||
|
|
|
|
i |
|
|
|
|
j |
|||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
1 |
|
1 |
|
|
|
1 |
1 |
|
|
|
|
2 |
1 |
|
|
|
|
2 |
1 |
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= −5i +11j − k . □
Пример 2. Вычислить площадь параллелограмма,
построенного на векторах a = 5 |
|
+ 3 |
|
|
|
− 4 |
|
|
|
и |
|
= 3 |
|
− 2 |
|
+ 7 |
|
. |
||||||||||||||||||||||
|
|
|
k |
|
b |
k |
||||||||||||||||||||||||||||||||||
i |
|
j |
i |
j |
||||||||||||||||||||||||||||||||||||
|
Решение. Находим векторное произведение векторов |
|||||||||||||||||||||||||||||||||||||||
a и |
|
: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
b |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
i |
|
|
j |
|
|
k |
|
|
|
|
3 |
−4 |
|
|
|
|
5 |
4 |
|
|
|
|
|
5 |
3 |
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
a × |
|
= |
5 |
3 −4 |
= |
|
|
− |
|
|
|
+ |
|
|
= |
|
|
|
|
|||||||||||||||||||
|
|
b |
k |
|
|
|
|
|||||||||||||||||||||||||||||||||
|
|
i |
j |
|
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
3 |
−2 |
7 |
|
|
|
|
−2 |
7 |
|
3 |
7 |
|
|
3 |
−2 |
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
=13i − 47 j −19k . □
Так как модуль векторного произведения двух векторов равен площади построенного на них
параллелограмма, |
|
то |
S = |
a × |
|
|
= |
||||
b |
|||||||||||
|
|
|
|
|
|
|
|||||
= 132 + 472 +192 = |
|
= |
|
(кв.ед.). □ |
|||||||
169 + 2209 + 361 |
2739 |
||||||||||
|
Пример 3. |
Вычислить площадь |
треугольника с |
||||||||
вершинами A(1;2;3), B(2;3;4), C(3;4;6).
Решение. Находим векторы AB и AC :
107

AB = (2 -1)i + (3 - 2) j + (4 - 3)k = i + j + k ,
AC = (3 -1)i + (4 - 2) j + (6 - 3)k = 2i + 2 j + 3k .
Площадь треугольника АВС равна половине площади
параллелограмма, построенного на векторах AB и AC , поэтому находим векторное произведение этих векторов:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
´ |
|
|
|
|
|
|
= |
|
i |
|
|
|
|
j |
|
|
|
|
k |
|
= |
|
|
|
|
1 1 |
|
- |
|
|
|
|
|
1 1 |
|
+ k |
|
1 1 |
|
= |
|
|
- |
|
|
|
+ 0× |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
AB |
AC |
1 1 1 |
i |
|
|
|
j |
|
|
|
|
|
|
|
i |
|
|
j |
|
k |
. |
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
2 |
3 |
|
|
|
|
|
|
|
|
2 |
|
3 |
|
|
|
|
|
|
|
|
|
|
|
2 |
3 |
|
|
|
|
|
|
|
|
2 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
Следовательно, |
SABC = |
|
|
|
|
|
|
AB ´ AC |
|
= |
|
|
|
|
1+1 = |
|
|
|
|
|
|
|
|
(кв.ед.). □ |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
2 |
|
2 |
2 |
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
Пример 4. Вычислить площадь параллелограмма, |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
построенного на векторах |
2a + |
|
|
|
|
и |
|
4a + 3 |
|
|
|
, если |
|
a |
|
= |
|
|
|
|
|
=1, |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
b |
|
b |
|
|
|
b |
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
а угол между векторами a |
и |
|
|
|
|
|
равен 30o . |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
b |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Имеем |
|||||||||||||||||||||||||||||||||||
(2a + |
|
|
|
) ´ (4a + 3 |
|
|
|
|
) = 8a ´ a + |
|
´ 4a + 6a ´ |
|
|
|
+ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
b |
b |
b |
b |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
+3 |
|
|
|
|
|
´ |
|
|
|
= 8×0 - 4a ´ |
|
|
+ 6a ´ |
|
+ 3×0 = 2a ´ |
|
|
|
|
|
|
|
|
|
|
(поскольку |
|
|
a × a = |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
b |
b |
b |
b |
b |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
´ |
|
|
|
|
= 0, |
|
|
´ a = -a ´ |
|
|
). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||
b |
b |
b |
b |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
Итак, S = 2 |
|
a ´ |
|
|
|
|
= 2 ×1×1×sin30o =1 (кв.ед.). □ |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
b |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
Пример |
|
|
|
|
5. |
|
|
|
|
|
|
|
|
|
|
|
|
Даны |
|
|
|
|
|
вершины |
|
|
|
|
|
|
|
|
|
|
|
|
|
треугольника |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
A(1;−1;2), B(5;−6;2) |
|
и C(1;3;−1). Вычислить длину его высоты, |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
опущенной из вершины В на сторону АС. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение. |
|
|
|
|
Найдем |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
и |
|
|
|
|
´ |
|
|
|
|
. |
|
|
Имеем |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
AC |
|
|
|
|
|
|
|
AB |
AC |
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
= (0;4;-3) , |
|
|
|
|
|
|
|
|
|
|
= (4;-5;0). |
Тогда |
|
|
|
|
|
|
|
|
|
|
|
= |
42 + (-3)2 = |
|
|
|
|
|
|
|
|
|
= 5, |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
AC |
|
|
|
AB |
|
|
|
|
AC |
|
|
|
|
|
25 |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
´ |
|
|
|
= |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
AB |
AC |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
i |
|
|
|
|
|
|
j |
|
|
|
k |
|
|
|
|
-5 0 |
|
|
|
|
|
|
4 0 |
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
-5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||
= |
4 -5 0 |
= |
i |
|
- |
j |
|
+ |
k |
|
|
|
|
|
=15 |
i |
+12 |
j |
+16 |
k |
, |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
0 |
|
|
4 |
|
|
|
|
-3 |
|
|
|
|
|
|
|
4 |
|
|
|
-3 |
|
|
|
|
|
|
|
0 |
|
-3 |
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
108
AB × AC = 15i +12 j +16k = 
 152 +122 +162 =
152 +122 +162 = 
 625 = 25.
625 = 25.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
AB |
× |
AC |
|
25 |
|
|
|
|
|
|
||||||||||||
|
|
Тогда длина искомой высоты h = |
|
|
|
|
|
|
|
|
|
|
|
= |
|
|
|
= 5. □ |
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5 |
|
|
|
|||||||||||||||||||||
|
|
|
|
AC |
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
Пример 6. Даны три силы F1 = (2;−1;−3), F2 = (3;2;−1) |
|
и |
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
C(−1;4;−2). |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
F3 = (−4;1;3), приложенных |
к точке |
|
|
Определить |
||||||||||||||||||||||||||||||||||
величину и направляющие косинусы момента |
|
|
|
|||||||||||||||||||||||||||||||||||
M |
|
|||||||||||||||||||||||||||||||||||||
равнодействующей этих сил относительно точки A(2;3;−1). |
||||||||||||||||||||||||||||||||||||||
|
|
Решение. Найдем координаты вектора |
|
− |
||||||||||||||||||||||||||||||||||
|
|
R |
||||||||||||||||||||||||||||||||||||
равнодействующей сил |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
F1, F2 , F3 : |
R = F1 + F2 + F3 = (1;2;−1). |
|||||||||||||||||||||||||||||||||||||
Далее находим момент силы R относительно точки А. Так как AC = (−3;1;−1), то, учитывая, что момент силы M
относительно данной точки есть векторное произведение этой силы на радиус-вектор точки приложения, будем иметь:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
i |
|
|
|
j |
|
|
|
|
k |
|
|
|
|
|
|
|
1 −1 |
|
− |
|
|
−3 |
−1 |
|
+ |
|
|
−3 1 |
|
= |
|
− 4 |
|
|
− 7 |
|
. |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
M |
= AC × R = |
−3 1 −1 |
= |
|
i |
|
|
j |
|
|
k |
|
|
i |
|
j |
k |
|||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
2 |
|
|
−1 |
|
|
|
|
|
|
2 |
|
|
−1 |
|
|
|
|
1 |
−1 |
|
|
1 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
Тогда |
|
|
|
|
|
|
= |
|
|
|
|
|
|
|
= |
|
|
|
|
|
|
Пронормировав |
вектор |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||
M |
|
|
|
|
1+16 + 49 |
|
|
66. |
|
|
|
M |
, |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
имеем |
|
|
|
|
|
= |
1 |
|
|
|
− |
4 |
|
|
|
|
− |
|
7 |
|
|
|
, |
то |
есть |
|
|
cosα = |
|
|
1 |
|
, |
|
||||||||||||||||||||||||||||||||||
M |
0 |
|
|
i |
|
|
|
j |
|
|
k |
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||
66 |
|
66 |
|
66 |
|
|
66 |
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
cos β = − |
4 |
|
|
|
, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
66 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
cosγ = − |
|
7 |
|
|
|
|
. □ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
66 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
Из |
|
|
|
свойства |
4) |
|
|
и |
|
|
формулы |
(5) |
|
вытекает, что |
|
|
|
два |
|||||||||||||||||||||||||||||||||||||||||||||||
ненулевых вектора a и b коллинеарны тогда и только тогда, когда для их координат выполняется равенство
a1 = a2 = a3 . b1 b2 b3
109

|
|
|
Пример 7. Даны векторы a = 2 |
i |
+ 2 |
j |
+ |
k |
и |
|||||
|
|
= 4 |
|
+ 4 |
|
+ |
|
. Являются ли векторы коллинеарными? |
|
|||||
b |
k |
|
||||||||||||
|
i |
j |
|
|||||||||||
Решение. Проверим условие коллинеарности векторов в координатах ортонормированного базиса:
24 = 24 ¹ 11.
Векторы a и b неколлинеарны. □
20 . Смешанное произведение векторов. Смешанным произведением векторов a, b и c называют скалярное произведение вектора a ×b на
вектор c , т.е. (a ×b ) c . Обозначают также abc или (a, b , c ). Смешанное произведение (a ×b ) c равно объему V
параллелепипеда, построенного на векторах a,b ,c , взятому со знаком «+»,
если тройка a,b ,c – правая, со знаком «–», если тройка a,b ,c – левая.
Смешанное произведение не меняется при круговой перестановке его сомножителей; перестановка двух соседних сомножителей меняет знак произведения на противоположный, т.е.
a b c = b c a = c a b = −(b a c ) = −(c b a) = −(a c b ).
Необходимым и достаточным условием компланарности векторов a,b ,c является равенство нулю их смешанного произведения:
Если векторы a, |
|
,c |
|
|
ab |
c = 0 . |
|
|
|
(6) |
|||||
|
|
заданы |
своими координатами, |
т.е. |
|||||||||||
b |
|||||||||||||||
a = (a1;a2;a3 ), |
|
= (b1;b2;b3 ), |
c = (c1;c2;c3 ), то |
|
|||||||||||
b |
|
||||||||||||||
|
|
(a × |
|
) c = |
|
a1 |
a2 |
a3 |
|
|
|
||||
|
|
|
|
|
|
||||||||||
|
|
b |
|
b1 |
b2 |
b3 |
|
. |
(7) |
||||||
|
|
|
|
|
|
|
|
|
|
c1 |
c2 |
c3 |
|
|
|
Отметим также, что объем треугольной пирамиды, образованной векторами a,b ,c , равен 16 ab c .
110
