
БНТУ / Математика / Конспект лекций по математике для студентов инженерно-технических специальностей
.pdf
функция y = x , непрерывна в точке x = 0 , но не является дифференцируемой в этой точке,
т.к. f ′(0 − 0)≠ f ′(0 + 0).
|
Рассмотрим функцию |
y = 3 |
x ; |
она |
определена и |
непрерывна |
|
x R . |
Найдем |
|||||||||||||||||
производную этой функции |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
У |
|
||||||||||
|
|
3 |
x + ∆x − 3 x |
|
|
|
|
|
|
x + ∆x − x |
|
|
|
|
|
|
||||||||||
f '(x) = lim |
|
|
|
|
|
|
|
= lim |
|
|
|
|
|
|
|
|
|
|
|
= |
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
3 |
2 |
|
|
|
|
||||||
|
∆x→0 |
|
∆x |
|
|
|
|
∆x→0 ∆x(3 (x + ∆x) + 3 x(x + ∆x) + |
|
Т |
|
|
||||||||||||||
|
|
|
|
|
|
|
x |
) |
|
|
|
|
||||||||||||||
= lim |
|
|
|
1 |
|
|
|
|
|
|
= |
|
1 |
. |
|
|
Н |
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
33 |
|
|
|
|
|
|
|||||||||
∆x→0 3 (x + ∆x)2 + 3 x(x + ∆x) + 3 x2 |
|
x2 |
|
Б |
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
х = 0. |
|
||
|
В точке x = 0 f ′(0)= ∞, т.е. не существует конечной производной в точке |
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
й |
|
|
|
|
|
|
|
|
||
§ 6. Основные правила дифференцирования |
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
Пусть функции |
|
|
u (x) и v(x) |
и |
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
дифференцируемы x (a,b). |
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
Рассмотрим |
|
|
|
|
|
|
|
|
|
|
|
|
||||
1. Производная алгебраической суммы |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
Производная алгебраической суммы конечного числа дифференцируемых |
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
т |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
функций равна алгебраическойрсумме производных этих функций. |
|
|
||||||||||||||||||||||||
|
|
|
|
|
значению |
|
|
|
|
|
функцию |
y = u (x)+ v(x). |
Дадим |
|||||||||||||
|
Доказательство. |
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
з |
|
|
|
х |
приращение |
∆х, |
тогда |
|
функции u (x) |
и |
||||||||||||
фиксированному |
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
определению |
|
|
|
|
|
|
|
|
|
|
|
|
∆u и |
∆v , и функция |
у |
|||||||||
v(x)получают приращения, соответственно равные |
||||||||||||||||||||||||||
|
п |
|
|
|
∆y |
= ∆u + ∆v . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
получает приращение |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
По |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
е |
|
|
y'= lim |
∆x = lim |
∆u + ∆v |
= lim |
∆u + lim |
∆v |
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
∆x |
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
∆x→0 |
∆y |
∆x→0 |
|
∆x |
|
∆x→0 |
∆x |
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∆x→0 |
|
|
|
|
|
|
|
|
Т.к. функции u (x) и v |
(x) |
дифференцируемые, то |
|
|
|
|
|
|
|
|
||||||||||||||||
Р |
|
|
|
|
|
|
|
|
|
|
lim |
∆u |
= u′, |
lim |
∆v = v' . |
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
∆x→0 |
∆x |
|
|
|
∆x→0 |
∆x |
|
|
|
|
|
|
|
|
|
Окончательно получим
236
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y |
′ |
|
|
|
|
|
′ |
|
|
′ |
|
|
′ |
|
|
|
|
(6.6) |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= (u + v) = u |
|
+ v |
|
|
|
|
|||||||||||||
2. TПроизводная произведения двух дифференцируемых функцийT |
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
Производная произведения двух дифференцируемых функций равна |
||||||||||||||||||||||||||||||||||||
сумме |
|
произведений |
производной |
|
первого |
сомножителя |
на |
|
второй |
и |
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
У |
|
||
производной второго сомножителя на первый, т.е. если y = uv , то y |
′ |
′ |
′ |
||||||||||||||||||||||||||||||||||
|
= u v + v u . |
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Т |
|
||||
|
Доказательство. Пусть y = u (x)v(x). Если х получает приращение |
|
∆x |
, |
то функции |
||||||||||||||||||||||||||||||||
y, u, |
v |
|
получают приращения |
|
|
|
соответственно |
|
|
∆y, ∆u, ∆v . |
|
|
|
При этом |
|||||||||||||||||||||||
∆y = (u + ∆u)(v + ∆v)−uv = v∆u + u∆v + ∆u∆v . |
|
|
|
|
|
|
Н |
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
lim |
∆y |
= vlim |
|
∆u |
+ u lim |
∆v |
|
+ lim |
∆u lim∆v . |
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
∆x→0 |
∆x |
|
|
∆x→0 |
|
∆x |
|
|
|
∆x→0 |
∆x |
|
|
∆x→0 |
∆v ∆x→0 |
|
|
|
|
|
||||||||
Учитывая, что |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
й |
|
|
|
|
|
|
||||||||||
|
|
|
|
lim |
∆y |
= y', |
|
lim |
∆u |
= u |
', |
lim |
∆v = v', |
Б∆v = 0 |
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
lim |
|
|
|
|
|
|
|||||||||
|
|
|
|
∆x→0 ∆x |
|
|
|
|
∆x→0 ∆x |
|
|
|
|
|
(и) |
|
|
∆x→0 |
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
∆x→0 |
∆x |
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
р |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
(так как функция v = v(x) непрерывна), окончательно получим: |
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
конечного |
|
|
′ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y |
′ |
= |
uv |
|
′ |
|
|
|
|
′ |
|
|
|
|
|
(6.7) |
|||||
|
|
|
|
|
|
|
|
|
|
т |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
Правило дифференцирования произведения двух функций распространяется |
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
произведения |
|
|
числа функций. Так, например, |
|
|
|
|
|
||||||||||||||||||||||
на произведение любого |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
з |
|
|
|
|
′ |
|
|
|
|
|
|
′ |
|
|
|
′ |
|
|
|
′ |
|
′ |
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
y = (uvw) |
= u vw + uv w + uvw , |
|
|
|
|
|
||||||||||||||||||||||
|
|
произведений |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
нескольких дифференцируемых функций равна |
||||||||||||||||||||||||||||
т.е. производная |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
сумме |
|
|
|
|
|
|
|
производной каждой из них на все остальные. |
|
|
|
|
|
||||||||||||||||||||||||
|
п |
|
|
|
|
|
|
v = c |
|
(c −const ), то |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
В частности, если |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
е |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
′ |
|
′ |
+ cu |
′ |
|
|
|
′ |
, |
|
|
|
|
(6.8) |
|||||
Р |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(cu) |
= c u |
|
= cu |
|
|
|
|
||||||||||||||
|
|
′ |
= 0 . Отсюда следует, |
что постоянный множитель можно выносить за |
|||||||||||||||||||||||||||||||||
так как c |
|||||||||||||||||||||||||||||||||||||
знак производной. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
3. Производная частного функций |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
Производная дроби (частного двух дифференцируемых функций) равна |
||||||||||||||||||||||||||||||||||||
дроби, у которой знаменатель равен квадрату знаменателя данной дроби, а |
|||||||||||||||||||||||||||||||||||||
числитель |
равен разности |
между |
|
|
|
произведением производной |
|
числителя |
на |
||||||||||||||||||||||||||||
237
знаменатель и произведением числителя на производную знаменателя, т.е., если
y = u |
, где v ≠ 0 , то |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
v |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y'= u'v − uv' . |
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
v |
2 |
|
|
|
|
|
|
|
|
|
У |
|
|
|
Доказательство. Пусть u = u (x) и v = v(x) |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
– дифференцируемые функции, v(x)≠ 0 . |
||||||||||||||||||||||||||||
Дадим фиксированному значению аргумента х приращение ∆x , и найдем приращение функции |
||||||||||||||||||||||||||||||
у: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Т |
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
u + ∆u u v∆u − u∆v |
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
∆y = v + ∆v − v |
= v(v + ∆v) . |
|
|||||||||||||||||
Тогда |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Б |
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Н∆v |
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
∆u |
|
|
∆v |
|
|
|
|
|
∆u |
|
|
||||||
|
|
|
|
|
|
|
|
|
∆y |
|
|
v ∆x − u |
й |
|
∆x |
− u lim∆x→0 ∆x |
|
|
|
|||||||||||
|
|
|
|
|
|
|
lim |
∆x |
= lim |
|
|
= |
|
|
|
. |
|
|
||||||||||||
|
|
|
|
|
|
|
∆x→0 |
∆x→0 v(v + ∆v) |
|
|
|
v lim (v + ∆v) |
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∆x→0 |
|
|
|
|
|
||
Следовательно, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
тогда |
= |
u ′ |
= |
u 'v −uv' |
|
|
|
|
|
(6.9) |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
y ' |
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
и |
v |
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
т |
|
|
|
v |
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
р |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
4. Производная сложной функции |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
и |
(x), |
|
|
у |
является сложной функцией независимой |
||||||||||||||||||
|
|
Пусть y = f (u), u = u |
|
|
||||||||||||||||||||||||||
переменной |
|
з |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
x, |
u – промежуточная функция. При этом известна производная |
||||||||||||||||||||||||||||
|
|
о |
|
|
|
|
х |
и производная |
|
функции |
f (u) в |
точке |
u , |
|||||||||||||||||
функции |
u |
(x) |
в точке |
|
|
|
||||||||||||||||||||||||
|
п |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
соответствующей точке х. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
приращению |
|
y′ = fu′(u)u′(x). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
Тогда |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
Доказательство. Дадим фиксированному значению аргумента х приращение ∆x . Этому |
||||||||||||||||||||||||||||
|
|
|
|
соответствует |
приращение |
∆u |
функции |
u (x) |
и приращение |
∆y функции |
||||||||||||||||||||
y = f |
(u). Составим отношение |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
Р |
|
|
|
|
|
|
|
|
|
|
|
∆y |
= |
∆f |
|
∆u . |
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
∆x |
|
|
∆u |
|
∆x |
|
|
|
|
|
|
|
|
|
|
|||
|
|
При |
|
∆x → 0 приращения |
∆u , |
∆f |
стремятся к |
|
нулю. |
Так как |
u (x), |
f (u) |
||||||||||||||||||
дифференцируемые функции, то |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
238
|
|
|
|
|
lim |
∆u |
= u′(x), |
lim |
∆f = fu′(u) . |
|
|
|
||||||||||
|
|
|
|
|
∆x→0 |
∆x |
|
|
|
|
∆x→0 |
∆u |
|
|
|
|
||||||
Следовательно, если y = f (u(x)) , то |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
y ' = fu′(u)u′(x) |
|
|
|
(6.10) |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
У |
|
Итак, производная сложной функции равна произведению производной |
|||||||||||||||||||||
этой функции по промежуточному аргументу и производной промежуточного |
||||||||||||||||||||||
аргумента по x. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Т |
||||
5. Производная обратной функции |
|
|
|
|
|
|
|
|
|
|
|
Н |
|
|||||||||
|
Пусть функция y = f (x) монотонна на отрезке [a,b]. Функции y = f (x) и |
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Б |
|
|
|
|
x =ϕ( y) - взаимно обратные дифференцируемые функции и y′x |
≠ 0. Тогда |
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
x′y = |
|
1 |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y′x |
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
∆x |
|
1 |
и′ |
∆x = |
1 |
|
|
|
|||||||
|
Доказательство. Так как |
|
|
= |
∆y |
, то |
|
lim |
∆y |
. Откуда следует |
||||||||||||
|
|
|
|
|
|
|
∆y |
|
|
∆y→0 |
∆y |
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
∆x |
|
|
йlim∆x→0 ∆x |
|
|
|
|||||||
|
|
|
|
|
|
|
|
р |
|
|
|
1 |
|
|
|
|
|
|||||
|
|
|
|
|
т |
|
|
|
xy |
= |
|
y′x |
, |
|
|
|
(6.11) |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
т.е. производная обратной функции равна обратной величине производной данной |
||||||||||||||||||||||
функции. |
|
и |
о |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
з |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
о |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
§ 7 Производные основных элементарных функций |
|
|
|
|||||||||||||||||||
|
п |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
е |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1. Производная логарифмической функции |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
Р |
Пусть |
y = loga x , где |
a > 0, |
a ≠1. |
Дадим |
фиксированному значению |
||||||||||||||||
x D( y) приращение ∆x , тогда |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
∆y = loga (x + ∆x)− loga x = loga |
|
x + ∆x |
|
|
∆x |
|
|||||||||||||
|
|
|
|
|
|
= loga 1+ |
. |
|
||||||||||||||
|
|
|
|
|
x |
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
По определению
239
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
+ |
|
∆x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
loga |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
∆y |
|
|
|
|
|
|
x |
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∆x ∆x |
|
|
1 |
|
|
|
|
1 |
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
y ' = lim |
|
= lim |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= |
|
|
loga lim 1 |
+ |
|
|
|
|
|
|
|
|
= |
|
|
loga e = |
|
|
|
|
|
. |
|
|
||||||||||||||||||||
|
∆x |
|
|
|
|
|
|
|
∆x |
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
x |
|
|
xln a |
|
|
|||||||||||||||||||||||||||||||||
|
|
∆x→0 |
|
|
|
∆x→0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∆x→0 |
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
Итак, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y = loga x |
|
|
|
|
|
y'= 1 loga e = |
|
|
|
|
1 |
|
. |
|
|
|
|
У |
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
xln a |
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
Для сложной функции y = loga u(x) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
y'= |
|
|
|
1 |
|
|
loga e u'(x) = |
|
|
|
|
|
1 |
|
|
|
|
u'(x) . |
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
u(x) |
|
|
u(x)ln a |
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Т |
|
|
|
||||||||||||||||||
В частном случае при |
a = e |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y = ln u(x) y'= |
1 |
u'(x) . |
Н |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
u(x) |
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Б |
|
|
|
|
|
|
|
|
|
|
||||||||||||||
2. Производная степенной функции |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
y = (u(x))n , |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
Пусть |
|
|
|
n R . |
|
Рассмотрим |
случай, |
когда u (x)> 0 . Тогда |
|||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ln y = nlnu(x). Дифференцируем обе частийполученного равенства по правилу |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
дифференцирования сложной функции, |
|
|
|
|
|
|
|
|
y |
функцией от x: |
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
считая |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
′ |
|
|
|
|
|
|
′ |
|
|
|
|
|
|
|
|
y′ |
|
nu′(x) |
|
|
|
|
|
|
|
|
|
′ |
|
|
|
|
|
|
nu′(x) |
|
|
|
n−1 |
|
′ |
|
|
|
|||||||||||||||
|
|
(ln y) |
= n(ln u(x)) |
|
|
|
|
|
|
|
|
|
|
р= |
|
|
|
y |
|
|
= y |
|
u(x) |
= n(u(x)) |
|
|
|
u |
(x) . |
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y u(x) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
о |
|
|
n |
|
|
представим в виде |
y = (−1) |
n |
(v(x)) |
n |
, где |
||||||||||||||||||||||||||||||||||
Пусть u (x)< 0 , тогда функцию y |
= (u(x)) |
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
′ |
|
|
|
|
|
|
т |
|
|
|
|
|
|
|
|
|
|
|
|
|
′ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
v(x) > 0; y |
= (−1) |
n |
n(v(x)) |
n−1 ′ |
|
|
|
= n(u(x)) |
n−1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
v |
(x) |
|
|
u |
(x) . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
Итак, |
|
|
|
|
|
|
и |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
з |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
′ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
′ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
о |
|
|
|
y = (u(x)) |
n |
|
|
|
y |
= n(u(x)) |
n−1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
u |
(x) . |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
3. Производная показательной функции |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
п |
|
|
|
|
u( x) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
u (x) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
y = a , |
|
где |
a > 0, a ≠1, |
|
|
- непрерывная функция. Тогда |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
Пусть |
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
еln y = u (x)ln a . Дифференцируем обе части полученного равенства: |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
Р |
|
|
|
|
|
|
|
|
|
|
|
|
y′ |
|
′ |
|
|
|
|
|
|
|
|
|
|
|
|
|
y |
′ |
|
= a |
u( x) |
|
ln a . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
= u |
(x)ln a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
Итак, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y = au( x) |
|
|
y'= au( x) ln au'(x) . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
240
4. Производные тригонометрических функций |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
В примере 6.2 было получено |
|
y = sin x |
|
|
|
y′ = cos x . |
|
|
|
|
|
|||||||||||||||||||||||||||
|
Для сложной функции |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
y = sin u (x) |
|
|
y'= cosu(x)u'(x) . |
|
|
|
|
|
|
У |
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Пусть y = cos x . Дадим фиксированному значению x приращение ∆x , тогда |
|||||||||||||||||||||||||||||||||||||||
|
|
|
∆y = cos(x + ∆x) − cos x = −2sin x + |
∆x |
sin ∆x . |
Т |
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
2 |
|
|
|
|
|
|||
По определению |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Н |
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
sin |
∆x |
|
|
|
|
|
|
Б |
|
|
|
|
|
|
|
|||||||||
|
|
y′=lim |
∆y |
= − lim |
|
2 |
|
|
|
|
|
|
|
∆x |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
∆x |
|
|
|
sin x + |
|
2 |
|
= − sin x . |
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
∆x→0 |
|
|
|
∆x→0 |
|
|
∆x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Итак, |
|
|
|
|
|
|
|
|
|
|
|
|
|
и |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
y = cos x |
|
|
|
|
y |
′ |
= −sin x . |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
Для сложной функции |
|
|
|
р |
й |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
y = cosu(x) |
|
y'= −sin u(x)u'(x) . |
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
т |
|
то по правилу дифференцирования частного, |
|||||||||||||||||||||||||||||||||
Пусть y = tgx ; так как |
tgx |
= sin x , |
|||||||||||||||||||||||||||||||||||||
|
|
|
и |
|
cos x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
получим |
|
о |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
з |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
sin x ′ |
|
|
cos xcos x −sin x(−sin x) |
|
1 |
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
y ' |
|
|
|
|
|
|
|
. |
|
|||||||||||||||||||||||||||
|
|
о |
= |
|
|
|
|
= |
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
= |
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
cos |
|
x |
|
|
|
|
|
|
cos |
2 |
x |
|
|||||||||||||||
|
|
|
cos x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
Итак, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y = tgx |
|
|
|
|
y'= |
|
|
1 |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
cos2 x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
пДля сложной функции |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
е |
|
|
|
|
y = tgu(x) |
|
|
|
y'= |
|
|
u'(x) |
. |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
РАналогично для y = ctgx |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
cos2 u(x) |
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
cos x ′ |
|
−sin xsin x −cos xcos x |
|
|
|
1 |
|
|
|
|
|
||||||||||||||||||||||||
|
|
y ' = |
|
|
|
|
= |
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
= − |
|
|
|
|
|
|
|
|
. |
|
||||
|
|
|
|
|
|
|
|
|
|
sin |
x |
|
|
|
|
|
|
|
|
sin |
2 |
x |
|
|
|||||||||||||||
|
|
|
|
sin x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
241

Итак, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y = ctgx |
|
|
|
y'= − |
|
|
|
1 |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
sin2 |
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Для сложной функции |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
y = ctgu(x) |
|
y'= − |
|
|
u'(x) |
. |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
sin2 u(x) |
|
|
|
|
|
|
πТ |
|
|
|
||||||||||||
5. Производные обратных тригонометрических функций |
|
|
|
|
|
|
|
π |
|
|
|
|
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
|
|
Пусть |
|
y = arcsin x |
|
имеет |
|
обратную |
|
функцию |
|
x = sin y , |
π |
|
π |
, |
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
У− ≤ y ≤ |
2 |
|||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
′ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
−1 ≤ x ≤1, x′y = cos y |
|
|
|
|
обращается |
в |
нуль |
Б |
, |
|
. |
По |
правилу |
||||||||||||||||||||||||||||||||||||||
не |
|
|
y |
− |
|
2 |
2 |
||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
дифференцирования обратной функции имеем |
|
|
|
|
|
|
|
|
|
|
|
Н |
|
|
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
yx = |
|
1 |
= |
|
1 |
|
|
|
= |
|
1 |
|
|
|
|
= |
|
|
|
|
1 |
|
|
. |
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x′y |
|
|
cos y |
и |
|
|
|
1− x2 |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
−sin2 |
|
y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
− |
π |
, |
π |
|
|
|
|
|
|
|
|
|
|
р |
й |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
В интервале |
2 |
2 |
|
cos y > 0 , поэтому перед квадратным корнем выбран знак |
|
||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
о |
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
“+”. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Итак, |
|
|
|
|
|
и |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y'= |
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
y = arcsin x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
о |
|
|
|
т |
|
|
|
|
|
|
|
|
|
|
|
1 − x2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
Для сложной функции |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
зy = arcsin u(x) |
|
y'= |
1 |
u'(x) . |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
е |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
− u2 (x) |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Аналогично доказывается |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
Р |
п |
|
|
|
|
|
|
|
y = arccosu(x) |
|
y'= − |
u'(x) . |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 − u2 (x) |
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
π |
|
|
π |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
Пусть y = arctgx, |
|
x = tgy , − |
2 < y < |
2 |
, − ∞ < x < +∞. Имеем |
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
y′x |
= |
|
1 |
|
|
= |
|
|
1 |
|
|
= cos2 |
y = |
|
1 |
|
|
|
= |
|
|
1 |
|
|
. |
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
x′y |
|
|
(tgy)' |
|
|
|
|
|
|
|
|
|
+ x2 |
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 + tg 2 y 1 |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
Итак,
242
|
|
|
|
|
|
y = arctgx |
|
|
|
|
|
|
y'= |
|
|
1 |
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
1 + x2 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Для сложной функции |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
y = arctgu(x) |
y'= |
|
|
u'(x) |
. |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
+ u2 (x) |
|
|
|
|
|
|
|
|
|
|
У |
||||||||||
Аналогично доказывается |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
y = arcctgu(x) |
|
|
|
|
y'= − |
|
u'(x) |
. |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 + u2 (x) |
|
|
|
|
|
|
|
|
|
|
|||||||||
6. Производные гиперболических функций |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Т |
||||||||||||||||||||
|
Пусть y = shx , тогда |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Н |
|
|
|
||||||||||||
|
|
|
|
|
|
ex − e−x ′ |
|
1 |
|
|
x |
|
|
|
|
−x |
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
(shx)′ = |
|
|
|
|
|
|
= |
|
|
(e + e |
|
) |
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
2 |
|
|
|
|
2 |
|
|
|
= chx . |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Б |
|
|
|
|
|
|
|
|
|
||||||||||
Итак, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
y = shx |
|
|
|
|
|
y'= chx . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
Для сложной функции |
|
|
|
|
|
|
|
|
|
|
|
й |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
и |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
y = shu(x) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
y'= chu(x)u'(x) . |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
р |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
Поступая аналогично, найдём производные остальных гиперболических |
|||||||||||||||||||||||||||||||||||||||
функций. |
|
|
|
|
о |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
т |
|
|
|
|
x |
|
|
−x |
|
′ |
|
|
|
|
x |
|
|
|
−x |
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
y = chx |
|
y′ = |
e |
|
+ e |
|
|
= e |
|
− e |
|
|
= shx , |
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
и |
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
з |
|
|
|
|
|
shx ′ |
|
|
chxchx − shxshx |
|
|
1 |
|
|
|
|
|
|
||||||||||||||||||||
|
о |
y = thx |
|
y′ = |
|
|
|
|
|
|
= |
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
= |
|
|
|
|
, |
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
ch |
x |
|
|
|
|
ch |
2 |
x |
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
chx |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
п y = cthx |
|
|
|
y ' = |
chx |
′ |
= |
shxshx − chxchx |
= − |
|
|
|
1 |
|
. |
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
sh |
2 |
x |
||||||||||||||||||||
е |
|
|
|
|
|
|
|
|
shx |
|
|
|
|
|
|
|
|
sh |
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
Полученные ранее правила дифференцирования и формулы объединим в |
|||||||||||||||||||||||||||||||||||||||
таблицы. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Р |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Таблица основных правил дифференцирования функций
1. y = c y′ = 0 .
2. y = cu y′ = cu′.
243
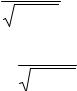
|
3. y = u + v |
|
|
y |
′ |
= u |
′ |
|
′ |
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
+ v . |
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
4. y = uv |
|
|
y |
′ |
|
|
′ |
|
|
|
′ |
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
= u v +uv . |
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
u |
|
|
|
|
|
|
|
|
|
|
|
′ |
|
|
′ |
|
|
|
′ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
u v |
−uv |
|
|
|
|
|
|
|
|
|
|||||||
|
5. y = v |
|
|
|
|
|
|
|
|
y |
|
|
= |
|
v2 |
|
|
. |
|
|
|
|
|
|
|
У |
||||||
|
6. y = f (u), u = u (x) |
|
|
|
|
|
y′ = fu′(u)u′(x). |
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
7. y = f (x) |
|
|
|
x =ϕ(y) |
|
y′x = |
1 |
. |
|
Т |
|||||||||||||||||||||
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x′y |
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Н |
|
||||
Таблица производных основных элементарных функций |
|
|||||||||||||||||||||||||||||||
|
|
|
||||||||||||||||||||||||||||||
1. (un )'= nun−1u', |
|
|
|
|
n R . |
|
|
|
|
|
|
|
|
|
|
Б |
|
|
||||||||||||||
2. (au )'= au ln au', |
a > 0, |
a ≠1. |
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
й |
|
|
|||||||||||||||||||||||||||
3. (eu )′ = euu' . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
и |
|
|
|
||||||||||||
4. |
(loga u)'= |
|
|
|
u' |
|
|
|
, |
|
|
a > 0, |
a ≠1. |
|
|
|
|
|||||||||||||||
|
u ln a |
|
|
р |
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
5. |
(lnu)'= u' . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
о |
|
|
|
|
|
|
|
|||||||||
|
|
|
u |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6. (sin u)'= cosu u'. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
u' |
|
|
|
|
и |
|
|
|
|
|
|
|
|
|
|
|||||||||
7. (cosu)'= −sin u |
u'. |
|
|
т |
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
з |
|
|
|
|
|
|
|
|
|||||||||||||||||
8. |
(tgu)'= |
|
u' |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
cos2 u |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
о |
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
9. |
(ctgu)'= − |
|
|
|
2 |
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
п |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
е |
|
|
|
|
sin u |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
10. (arcsinu)'= |
|
|
|
u' . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
1 − u |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
11. (arccosu)'= − |
|
|
|
|
u' . |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 − u2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
12. (arctgu)'= |
|
|
u' |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
1 + u2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
Р |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
13. (arcctgu)'= − |
|
|
|
|
u' |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
1 + u2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
14. (shu)'= chu u' .
244

15.(chu)'= shu u' .
16.(thu)'= chu2'u .
17.(cthu)'= − shu2'u .
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
У |
|
||
§ 8. Дифференцирование неявных функций |
|
|
|
|
|
|
Т |
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
Пусть функция y = f (x) |
задана уравнением |
F |
(x, y)= 0 т.е. уравнением, |
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Б |
|
|
|
|
|
|
||||
связывающим независимую переменную x c функцией y, не разрешенным |
|||||||||||||||||||||||||
относительно y . В этом случае говорят, что функция |
y = fН(x) задана неявно. |
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
й |
|
|
|
|
|
|
|
|
|
′ |
|||
|
|
|
Производную от функции F (x, y)= 0 |
можно найти дифференцированием |
|||||||||||||||||||||
по х обеих частей этого уравнения с учётом того, |
что |
|
y |
есть функция от |
x. |
||||||||||||||||||||
Полученное |
после дифференцирования уравнение |
будет |
содержать |
x, y, |
y . |
||||||||||||||||||||
|
|
|
|
|
|
|
|
по |
|
|
|
|
|
′ |
|
|
|
|
|
|
|
|
|||
Разрешая его относительно |
′ |
, найдёмипроизводную |
y |
функции y = f (x). |
|
||||||||||||||||||||
y |
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
т |
|
|
|
|
x + |
xy |
+ y = a , заданной неявно. |
|
||||||||||
|
|
|
Пример 6.3. Найти производнуюрфункции |
|
|||||||||||||||||||||
|
|
|
Решение. |
и |
|
|
|
|
x |
данную |
неявную |
функцию, |
получим: |
||||||||||||
|
|
|
Дифференцируя |
|
|
||||||||||||||||||||
|
y |
+ xy' |
|
из |
|
2 xy + y + y '(x + 2 |
xy ) |
|
|
|
y′ |
|
y + 2 |
xy |
|
|
|||||||||
1 + |
2 |
xy |
+ y'= 0 . |
Отсюда |
= 0 , |
= − |
x + 2 |
xy |
. |
|
|||||||||||||||
Выражая |
о |
|
|
|
|
и y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
xy |
уравнения через x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
е |
|
|
|
|
|
|
|
|
xy = a − x − y , |
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
получим: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Р |
п |
|
|
|
y'= − |
2a − 2x − y |
. |
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
2a − 2 y − x |
|
|
|
|
|
|
|
|
|
|
|
|
||
Отметим, что y'=ϕ(x, y).
245
