
БНТУ / Математика / Конспект лекций по математике для студентов инженерно-технических специальностей
.pdf
следовательно |
x = x′cosϕ − y′sinϕ. |
Аналогично |
y = OM sin(ϕ +α)= OM sinϕcosα + OM sinα cosϕ = y′cosϕ + x′sinϕ .
Таким образом получены формулы:
|
|
|
|
|
|
|
|
|
|
′ |
|
|
|
′ |
sinϕ |
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
x = x cosϕ |
|
− y |
|
|
|
|
|
|
(4.23) |
|||||||
|
|
|
|
|
|
|
|
|
|
′ |
|
|
|
′ |
cosϕ |
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
y = x sinϕ |
+ y |
|
|
|
|
|
У |
|||||||||
выражающие старые координаты через новые. |
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
Разрешив равенство (4.23) относительно х' и у', получим формулы: |
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
′ |
|
|
|
|
|
|
|
|
|
Т |
|
|||
|
|
|
|
|
|
|
|
|
|
x = xcosϕ + ysinϕ |
|
(4.24) |
||||||||||||
|
|
|
|
|
|
|
|
|
|
y′ = −xsinϕ + y cosϕ |
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
которые выражают новые координаты через старые. ФормулыН(4.23) и (4.24) будем |
||||||||||||||||||||||||
называть формулами поворота осей. |
|
|
|
|
|
|
|
Б |
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Эллипс, гипербола и парабола с осями, |
|
|
|
|
|
|
|
|
осям координат |
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
й |
|
|
|
|
|
||||
|
Рассмотрим эллипс с |
|
|
|
параллельными |
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
в точке |
О'( a;b), оси которого параллельны осям |
|||||||||||||||||||
координат (рис. 4.23). |
|
|
|
|
р |
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
y |
|
|
y′ |
|
|
центром |
|
|
|
|
Возьмём новую систему координат, |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
т |
|
|
|
начало |
которой находится в |
точке |
|||||||||||||
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
О'(α, β ), |
а |
оси |
О'х' и |
О'у' |
|
параллельны |
|||||||||
|
|
|
|
и |
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
x′ |
соответственно осям Ох и Оу и одинаково |
|||||||||||||||||
|
|
|
|
0 |
′ |
|
|
|
|
|||||||||||||||
|
|
|
з |
|
|
|
|
|
|
с ними направлены. |
|
|
|
|
||||||||||
|
|
о |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
0 |
|
|
|
|
|
|
x |
|
|
|
|
Так |
как |
новые |
оси |
координат |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
совпадают с осями эллипса, |
|
а его центр |
|||||||||||
|
п |
|
Рис. 4.23 |
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
находится |
в |
новом |
начале, |
то |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
е |
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
относительно новой системы координат уравнение эллипса будет каноническим: |
||||||||||||||||||||||||
Р |
|
|
|
|
|
|
|
|
|
2 |
|
|
|
2 |
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
x′ |
|
+ |
|
y′ |
=1. |
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
2 |
|
2 |
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
a |
|
|
|
b |
|
|
|
|
|
|
|
||
166
Чтобы получить уравнение эллипса в старой системе координат, надо воспользоваться формулами параллельного переноса осей:
x′ = x −α y′ = y − β .
Подставляя в уравнение эллипса вместо х' |
и |
|
|
|
|
|
|
|
|
|
Т |
|
||||||||
у' их выражения через х |
и у, получим |
|||||||||||||||||||
|
|
|
|
|
(x −α)2 |
+ |
(y − β)2 |
|
= |
1 |
Н |
|
(4.25) |
|||||||
|
|
|
|
|
a2 |
|
|
b2 |
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
У |
|||||
Аналогично можно показать, что уравнение гиперболы с центром в точке О'(α; β ) и |
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
Б |
|
|
|
||||
с осями симметрии, параллельными осям координат, имеет вид: |
|
|
|
|||||||||||||||||
|
|
|
|
|
(x −α) |
2 |
− (y − β) |
2 |
=1, |
|
|
|
(4.26) |
|||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
a2 |
|
й |
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
b2 |
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
и |
|
|
|
|
|
|
|
|
|
|
||||
если действительная ось параллельна оси Ох, |
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
(y − β)2 |
− |
(x − |
α)2 |
=1, |
|
|
|
(4.27) |
|||||||
|
|
|
|
о |
b |
2 |
|
|
a |
2 |
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
если действительная ось параллельна оси Оу. |
|
|
|
|
|
|
|
|
|
|
|
|||||||||
если ось симметрии параллельнаточкеоси Оу, и |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
Парабола с вершиной в |
рО'(α; β ) имеет уравнение: |
|
|
|
|||||||||||||||
|
|
|
и |
|
y − β |
= a(x −α)2 , |
|
|
|
|
(4.28) |
|||||||||
|
|
з |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
о |
|
|
|
x −α = a(y − β)2 , |
|
|
|
(4.29) |
||||||||||
если ось симметрии параллельна оси Ох, где |
a = ± |
1 |
|
|
|
|
|
|
|
|||||||||||
2 p . |
|
|
|
|
|
|||||||||||||||
члены |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Если в любом из уравнений (4.25) – (4.29) раскрыть скобки и привести подобные |
||||||||||||||||||||
|
п, то получится уравнение вида: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
Ax2 + Cy2 + Dx + Ey + F = 0 , |
|
|
|
|
|||||||||||||
которое является частным случаем общего уравнения: |
|
|
|
|
|
|||||||||||||||
Р |
|
|
Ax2 + Bxy + Cy2 + Dx + Ey + F = 0, |
|
|
|
|
|||||||||||||
167

которое называется общим уравнением кривой второго порядка на плоскости.
Упрощение общего уравнения кривой второго порядка в случае отсутствия члена с
произведением (X Y ) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
У |
|||||||||||||
|
|
Рассмотрим уравнение |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Т |
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
Н |
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
Ax2 + Cy2 + Dx + Ey + F = 0 . |
|
|
|
|
|
(4.30) |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Б |
|
|
|
|
|
|
|
|
|
|
|||
Выясним, какие кривые соответствуют этому уравнению. |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
Возможны следующие случаи: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
1. |
АС > 0 (эллиптический случай). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
Без ограничения общности можно считать, что А > 0 и С > 0. |
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
В уравнении (4.30) дополняем до полного квадрата члены, содержащие x2 и х, |
|||||||||||||||||||||||||||||
а также y2 |
и у, получим |
о |
|
й |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
( |
0 ) |
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
( |
0 ) |
2 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
A x − x |
и+C y − y |
|
|
= F |
|
|
|
|
|
|
|
|
|
|
|
|
(4.31) |
|||
|
|
Если |
|
|
|
|
|
т |
р |
|
|
|
|
(x − x |
0 |
)2 |
+ |
(y − y |
0 |
)2 |
|
=1, где |
|||||||||
|
|
F > 0 , то уравнение приводится к виду |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
1 |
|
|
и |
|
|
|
|
|
|
|
|
|
a2 |
|
|
|
|
|
|
b2 |
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
2 |
|
F1 |
|
|
2 |
|
F1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a = |
|
|
; |
b |
з |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
A |
|
|
|
|
C |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
о |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
Если |
F1 |
< |
0 , то уравнению (4.31) никакие действительные значения х и у не |
||||||||||||||||||||||||||
|
п |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
удовлетворяют, следовательно, этому уравнению соответствует пустое множество. |
|||||||||||||||||||||||||||||||
|
|
Если |
F = 0 , то уравнение (4.31) принимает вид |
A(x − x |
0 |
)2 + C(y − y |
0 |
)2 = 0 и |
|||||||||||||||||||||||
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
определяет точку M (x0 , y0 ). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
Р |
|
2. |
AC < 0 |
(гиперболический тип). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
Не |
нарушая общности, можно считать A > 0, C < 0. Как и в первом случае, |
||||||||||||||||||||||||||||||
уравнение (4.30) можно привести к виду (4.31).
168
|
Если F > 0 ,то уравнение (4.31) можно записать |
(x − x |
0 |
)2 |
− |
(y − y |
0 |
)2 |
=1. Оно |
||||||||||||||||||||||||
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a2 |
|
|
|
|
|
b2 |
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
определяет гиперболу, действительная ось которой параллельна оси Ох. |
У |
|
|||||||||||||||||||||||||||||||
|
Если F < 0 , |
|
то получим гиперболу |
|
(y − y |
0 |
)2 |
|
(x − x |
0 |
)2 |
|
|
|
|
||||||||||||||||||
|
|
|
− |
=1, действительная |
|||||||||||||||||||||||||||||
|
|
1 |
|
|
|
|
|
|
|
|
|
|
b |
2 |
|
|
|
|
a2 |
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
ось которой параллельна оси Оу. |
|
|
|
|
|
|
|
|
|
|
|
|
Н |
|
|
|
|
|
|
||||||||||||||
|
Если F1 = 0 , то уравнение (4.31) принимает вид |
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
Т |
|
|||||||||||||||||||||||||
|
|
|
|
|
|
A(x − x0 )2 + C(y − y0 )2 = 0 . |
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Б |
|
|
|
|
|
|
|
|
|||||
Докажем, что ему соответствует пара пересекающихся прямых. |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
Обозначим |
A = m2 , C = −n2 |
|
|
|
й |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
и запишем уравнение в виде: |
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
m |
2 |
(x |
|
2 |
− n |
2 |
|
|
|
|
2 |
= 0 , |
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
− x0 ) |
|
(y − y0 ) |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
или |
|
|
|
|
|
|
|
|
|
|
и |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
р0 |
|
0 |
|
|
|
|
|
− y0 ))= 0 . |
|
|
|
|
|
|
|
|||||||||
|
|
|
|
(m(x − x0 )− n(y |
− y0 ))(m(x − x0 )+ n(y |
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
о |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Это уравнение равносильно следующим двум: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
т |
|
|
|
|
|
|
|
)= 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
и |
|
|
m(x − x )− n(y − y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
m(x |
− x0 )+ n(y − y0 )= 0 , |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
з |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
каждое из которых определяет прямую, проходящую через точку M (x0 , y0 ). |
|
|
|||||||||||||||||||||||||||||||
3. |
|
о |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
АС = 0 (параболический тип). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
Предположим, что А≠ 0, С = 0, тогда уравнение (4.30) имеет вид |
|
|
|
|
|
|
|
||||||||||||||||||||||||||
и х дополногоквадрата, получим |
|
|
|
|
|
|
|
= 0 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
Ax2 + Dx + Ey + F |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
Можно считать, не нарушая общности, что А > 0. Дополнив члены, содержащие x |
|
||||||||||||||||||||||||||||||||
Р |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
е |
|
|
|
|
|
|
A(x − x0 )2 + Ey = F1 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
Если Е≠ 0, то уравнение можно записать в виде |
y − y0 = a(x − x0 )2 , |
которому |
||||||||||||||||||||||||||||||
соответствует парабола с осью симметрии, параллельной оси Оу.
169

|
Если Е = 0, F1 > 0 , то уравнение |
A(x − x0 )2 = F1 равносильно уравнениям |
||||||||||||||||
A(x − x0 )+ |
F1 = 0 и |
|
A(x − x0 )− |
F1 = 0 , которые определяют пару параллельных |
||||||||||||||
прямых. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Если Е |
= |
0 и |
|
F1 < 0 , |
то |
уравнение |
|
A(x − x0 )2 = F1 |
определяет |
пустое |
|||||||
множество. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Т |
|
||
|
Если E = 0 и F1 = 0 , то уравнение A(x − x0 )2 = 0 определяет пару совпадающихУ |
|||||||||||||||||
прямых x − x0 |
= 0 . |
|
|
|
|
|
|
|
|
|
|
|
Б |
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Если предположить, что А = 0, С ≠ 0, то повторив аналогично исследования, |
|||||||||||||||||
получим те же результаты. |
|
|
|
|
|
|
|
|
Н |
|
||||||||
|
Итак, уравнению (4.30) |
|
|
|
|
й |
|
|
||||||||||
|
могут соответствовать следующие фигуры: эллипс, |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
или |
|
|
|
|||||
гипербола, парабола, пара прямых, точка |
пустое множество. |
|
||||||||||||||||
содержащие x2 |
и х, а также |
y2 и уопределяетполных квадратов, получим: |
|
|
||||||||||||||
|
Пример 4.3. |
Рассмотрим уравнение |
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
9x2 + 4 y2 −18x + 24 y + 9 = 0 . |
|
|
|||||||||
Т.к. AC = 36 > 0 , |
|
|
|
до( ) |
|
( |
|
) |
|
|
эллиптического |
типа. Дополнив |
члены, |
|||||
то уравнение |
|
|
|
|
фигуру |
|
||||||||||||
|
|
|
|
|
|
т |
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
и |
|
2 + 4 |
|
y + 3 2 = 36 , или |
|
|
|||||||
|
|
|
з |
|
9 x −1 |
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
2 |
|
|
(y + |
|
2 |
|
|
|
|
|
|
точке |
|
|
|
(x −1) |
+ |
3) |
|
=1. |
|
|
||||||
|
|
|
|
|
4 |
|
|
9 |
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Этому уравнению в декартовой системе координат соответствует эллипс, центр которого |
||||||||||||||||||
|
п |
О'(1;-3), а полуоси равны соотаетственно 2 и 3. |
|
|
||||||||||||||
находится в |
|
|
||||||||||||||||
е |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
§7. Поверхности второго порядка |
|
|
|
|
|
|
|
|
|
|||||||||
Р |
Алгебраической поверхностью второго порядка называется поверхность, |
|||||||||||||||||
|
||||||||||||||||||
уравнение которой в декартовой прямоугольной системе координат имеет вид: |
||||||||||||||||||
|
|
Ax2 + By2 +Cz2 + 2Dxy + 2Exz + 2Fyz + 2Mx + 2Ny + 2Pz + L = 0 |
(4.32) |
|||||||||||||||
170

В этом уравнении не все коэффициенты при членах второго порядка равны
нулю. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
В |
общем |
|
случае |
может |
|
оказаться, что уравнение (4.32) |
определяет |
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
У |
||
вырожденную поверхность (пустое множество, точку, плоскость, пару плоскостей, |
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Т |
||||
прямую). Если же поверхность (4.32) невырождена, то с помощью преобразования |
||||||||||||||||||||||||||||||||||
координат (параллельного переноса и поворота осей координат в пространстве) и |
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Н |
|
|
|
|||
теории квадратичных форм её уравнение может быть приведено к ниже |
||||||||||||||||||||||||||||||||||
рассматриваемым поверхностям. |
|
|
|
|
|
|
|
|
|
|
|
|
Б |
|
|
|
|
|
|
|||||||||||||||
Эллипсоид |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
некоторой |
|
|
|
|
|
|
|
|
|||||||||||
Поверхность, уравнение которой в |
|
декартовой прямоугольной |
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
системе координат имеет вид |
|
р |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y2 |
|
z |
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
о |
x |
2 |
+ |
|
+ |
2 |
=1 |
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
2 |
2 |
c |
2 |
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
т |
|
|
иa b |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(4.33) |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
называется эллипсоидом. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
и |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Для исследования формы эллипсоида применим метод сечений. Пересечем |
||||||||||||||||||||||||||||||||||
эллипсоид плоскостями z = h . Линия, полученная в сечении, определяется системой |
||||||||||||||||||||||||||||||||||
|
о |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
z |
|
|
|
||||||
уравнений: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
xз2 y2 z2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
+ |
|
|
|
+ |
|
=1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a2 |
b2 |
|
c2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
е |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
b |
|
y |
|||||||
|
z = h |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
пВ плоскости z = h возьмем декартову |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
прямоугольную систему координат О'х'у', |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
начало |
которой |
|
|
находится |
|
в |
точке |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
a |
|
|
|
c |
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
РО'(0;0;h), |
а оси |
|
|
Ох' |
и |
|
Оу' |
имеют |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 4.24 |
|
|
|
|||
171
соответственно направления осей Ох и Оу. В этой системе координат линия, полученная в сечении, имеет уравнение
|
|
|
|
|
|
|
|
|
|
(x′)2 |
+ (y′)2 |
|
=1 − h2 . |
|
(4.34) |
|||||||||||
|
|
|
|
|
|
|
|
|
|
a2 |
|
b2 |
|
|
|
c2 |
|
|
|
|
У |
|||||
|
|
< c (c > 0), |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Т |
||||||
Если |
h |
то уравнение (4.34) определяет эллипс. При |
h = 0 полуоси |
|||||||||||||||||||||||
эллипса соответственно равны a и b. С возрастанием |
|
h |
от нуля до с полуоси эллипса |
|||||||||||||||||||||||
|
|
|
|
|
|
h |
|
= с, |
|
|
|
|
|
|
|
|
|
|
|
|
|
Н |
|
h |
|
> c |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
уменьшаются. |
Если |
|
|
то уравнение |
(4.34) |
|
определяет точку. При |
|
||||||||||||||||||
уравнение определяет пустое множество, т.е. плоскость не пересекается с |
||||||||||||||||||||||||||
эллипсоидом. |
Аналогичная |
картина |
имеет место |
|
при |
пересечении эллипсоида |
||||||||||||||||||||
плоскостями y = m, |
x = n. |
|
|
|
|
|
й |
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
(4.33),Бимеет вид, |
|
|
|
|
|||||||||||||
Таким образом, эллипсоид, заданный |
уравнением |
изображенный |
||||||||||||||||||||||||
на рис. 4.24. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
р |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Положительные числа a, b, c называются полуосями эллипсоида. В частном |
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
о |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
случае, если две полуоси равны, эллипсоид называется эллипсоидом вращения, так |
||||||||||||||||||||||||||
|
|
|
|
|
|
|
т |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
как он может быть получен вращением эллипса вокруг одной из осей. |
|
|
|
|
||||||||||||||||||||||
Если a = b = c , то уравнение (4.33) определяет сферу |
x2 + y2 |
+ z2 = a2 . |
||||||||||||||||||||||||
|
|
|
|
и |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Гиперболоиды |
з |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Поверхность |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
, уравнение которой в некоторой декартовой прямоугольной |
||||||||||||||||||||||
системе координат Оxyz имеет вид |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
называется |
|
|
|
|
|
|
|
|
|
x2 |
|
y2 |
|
z2 |
|
|
|
|
|
|
|
|
||||
п |
|
|
|
|
|
|
|
|
|
|
=1 |
|
(4.35) |
|||||||||||||
|
|
|
|
|
|
|
|
|
+ |
|
− |
|
|
|||||||||||||
|
|
|
|
|
|
|
|
a2 |
b2 |
c2 |
|
|||||||||||||||
|
|
|
однополостным гиперболоидом. |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
Пересечем гиперболоид плоскостью z = h . Выберем в плоскости z = h систему |
||||||||||||||||||||||||||
Ркоординат O'х'у', как это было сделано выше. В этой системе линия пересечения |
||||||||||||||||||||||||||
имеет вид
172

|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(x′)2 |
+ |
(y′)2 |
=1 + h2 . |
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a2 |
|
|
|
b2 |
|
|
c2 |
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
Это уравнение эллипса при любом h. При h = 0 эллипс имеет полуоси a и b. С |
||||||||||||||||||||||||||||||||||||||||||||||
возрастанием |
|
h |
|
|
полуоси |
эллипса |
увеличиваются. |
Пересечем |
однополостный |
||||||||||||||||||||||||||||||||||||||||
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||
гиперболоид |
плоскостью |
y = m . Выберем в |
этой |
плоскости декартову |
систему |
||||||||||||||||||||||||||||||||||||||||||||
координат О''х''z'', |
у которой начало координат находится в точке О''(0;m;0), а оси |
||||||||||||||||||||||||||||||||||||||||||||||||
′′ ′′ |
|
|
|
|
|
|
′′ |
′′ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
У |
|||||
|
|
|
|
|
|
имеют направления осей соответственно Ох и Оz. В этой системе |
|||||||||||||||||||||||||||||||||||||||||||
O x |
|
|
и оси O z |
|
|||||||||||||||||||||||||||||||||||||||||||||
координат линия, полученная в сечении, имеет вид |
|
|
|
|
|
|
|
Т |
|
||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x′′2 |
z′′2 |
|
|
m2 |
|
|
|
|
|
|
Н |
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
− |
|
|
|
=1 − b2 |
|
|
|
|
|
|
|
|
|
(4.36) |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a2 |
|
c2 |
|
|
|
|
|
|
|
|
|
||||||||||||||
При |
|
m |
|
< b |
(b > 0) |
|
уравнение (4.36) |
определяет гиперболу, |
при |
|
m |
|
= b |
– пару |
|||||||||||||||||||||||||||||||||||
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
m |
|
> b – |
|
|
|
|
|
Б |
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
пересекающихся прямых, а при |
|
|
|
|
|
|
, вершины которой находятся на |
||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||
оси О''z''. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
й |
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
Аналогичная |
|
картина имеет |
место |
при |
|
пересечении |
однополостного |
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
гиперболу |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
гиперболоида плоскостями x = h . |
р |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Однополостный |
гиперболоид |
имеет |
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
овид, изображенный на рис. 4.25. |
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
z |
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
т |
|
|
|
|
|
|
|
|
|
В |
частном |
|
случае, |
|
когда |
a = b, |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
и |
|
|
|
|
|
|
|
|
|
|
|
|
гиперболоид |
|
называется |
однополостным |
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
з |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
y |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
гиперболоидом вращения, так как может быть |
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
о |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
получен |
вращением |
гиперболы |
|
вокруг её |
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
мнимой оси. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
п |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Поверхности, |
|
которые |
|
в |
|
некоторой |
|||||||||||||||||
е |
|
|
Рис. 4.25 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
декартовой системе координат Oxyz задаются |
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
уравнениями |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
Р |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
x2 |
|
− |
y2 |
+ |
z2 |
|
=1 |
|
|
|
|
и |
|
|
− |
x2 |
+ |
y2 |
|
+ |
z2 |
|
=1 |
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
a2 |
|
b2 |
c2 |
|
|
|
|
|
|
a2 |
b2 |
c2 |
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
173
также являются однополостными гиперболоидами.
Поверхность, уравнение которой в некоторой декартовой системе координат
имеет вид |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
− |
|
x2 |
|
− |
|
y2 |
|
+ |
|
z2 |
=1 |
|
|
|
|
|
|
|
|
|
|
|
|
(4.37) |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
a2 |
|
b |
2 |
|
|
c2 |
|
|
|
|
|
Т |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
называется двуполостным гиперболоидом. |
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Н |
|
|
|
|
|
||||||
|
|
z |
|
|
|
|
|
|
|
Применив метод сечений, |
можно убедитьсяУ, что |
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
поверхность имеет вид, изображённый на рис. 4.26. |
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
Если a = b, |
|
|
|
|
|
|
|
|
|
|
|
|
|
Б |
|
|
|
|
|
|
называется |
|||||||||||||
|
|
|
|
|
|
|
|
|
двуполостный |
гиперболоид |
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
двуполостным гиперболоидом вращения, и может быть |
||||||||||||||||||||||||||||||||||
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
й |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
Рис. 4.26 |
|
|
y |
получен |
|
|
|
|
вращением |
|
гиперболы |
|
|
|
вокруг |
её |
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
a |
|
|
оb |
сиc |
|
|
|
|
a |
|
|
b |
|
|
|
c |
|
|
|
|||||||||||||||
x |
|
|
|
|
|
|
|
действительной |
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
Поверхности, задаваемые уравнениями |
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
р |
|
|
|
z |
|
|
|
|
|
|
|
|
x |
2 |
|
y2 |
|
|
z |
2 |
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
x |
2 |
− |
y |
2 |
|
− |
2 |
=1 и |
|
− |
+ |
− |
=1 |
|
|||||||||||||||||
|
|
|
|
|
|
|
|
о |
|
|
|
2 |
|
|
|
|
|
2 |
|
|
|
|
|
|
|
2 |
|
|
2 |
|
|
|
2 |
|
|
|||||||
|
|
|
|
|
|
|
являются |
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
также |
двуполостными гиперболоидами. |
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
Параболоиды |
|
|
уравнение |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
з |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
Поверхность |
|
|
|
|
которой |
в |
некоторой |
декартовой |
прямоугольной |
|||||||||||||||||||||||||||||||
|
|
|
, |
|
|
|
||||||||||||||||||||||||||||||||||||
системе координат имеет вид |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
е |
|
|
|
|
|
|
|
|
|
|
|
|
|
z = |
|
x2 |
|
|
+ |
|
y2 |
, |
|
|
|
|
|
|
|
|
|
|
|
(4.38) |
||||||||
Р |
|
z |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
p |
|
|
|
q |
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
п |
|
|
|
где pq > 0 , называется эллиптическим параболоидом. |
|
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
Применив |
|
|
метод |
|
|
|
сечений, |
легко |
|
убедиться, |
что |
|||||||||||||||||||||||
|
|
|
|
y |
|
поверхность имеет вид, изображённый на рис. 4.27. |
|
|
|
|||||||||||||||||||||||||||||||||
x
Рис. 4.27
174

Если p = q , то такой параболоид называется параболоидом вращения и может быть получен вращением параболы вокруг её оси симметрии. Поверхности, которые
в некоторой прямоугольной системе координат задаются уравнениями: |
У |
||||||||||
y = |
x2 |
+ |
z 2 |
и x = |
y2 |
+ |
z 2 |
, (pq > 0), |
|
||
p |
q |
p |
q |
Т |
|||||||
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|||||
также являются эллиптическими параболоидами.
Поверхность, уравнение которой в некоторой декартовой прямоугольной
системе координат имеет вид |
|
|
|
|
|
|
|
|
|
Н |
|
||||||||||
|
|
|
|
|
|
|
z = − |
|
x2 |
y2 |
(pq > 0), |
|
|||||||||
|
|
|
|
|
|
|
|
|
+ |
|
, |
(4.39) |
|||||||||
|
|
|
|
|
|
|
|
p |
q |
||||||||||||
называется гиперболическим параболоидом. |
|
Б |
|
|
|||||||||||||||||
|
Пусть p > 0, |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
q > 0 . Пересекая гиперболический параболоид плоскостью x = h |
||||||||||||||||||||
легко убедиться, |
что в |
сечении |
|
|
|
|
параболу при любом h. Пересекая |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
й |
|
|
|
|
|
||
параболоид плоскостью |
y = m , |
|
|
в сечении получим параболу, ветви которой |
|||||||||||||||||
направлены вниз при любом m. |
|
|
получим |
|
|
|
|
|
|
|
|||||||||||
р |
|
|
|
|
|
|
|
|
|||||||||||||
|
Рассуждая |
аналогично, |
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
убедиться в том, что при пересечении |
||||||||||||||||
гиперболического |
|
|
легкоплоскостью z = h (h ≠ 0) получим гиперболы, а при |
||||||||||||||||||
z = 0 – пару пересекающихсятпрямых. |
|
|
|
|
|
|
|
|
|
|
|||||||||||
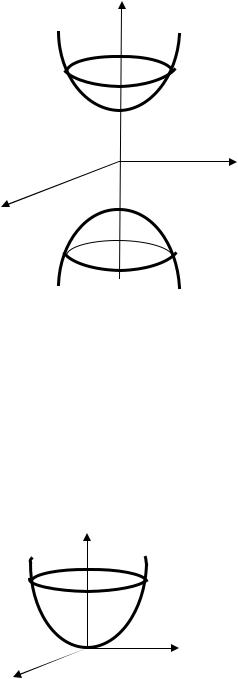
|
Гиперболический |
параболоид, заданный уравнением (4.39), имеет вид, |
|||||||||||||||||||
|
|
|
|
|
параболоида |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
изображённый на рис. 4.28. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
з |
|
|
|
|
|
|
|
Поверхности, которые в некоторой |
||||||||||
|
|
о |
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
z |
|
|
|
|
|
|
прямоугольной |
|
системе |
координат |
|||||||||
|
п |
|
|
|
|
|
|
|
y |
|
|
||||||||||
|
|
|
|
|
|
|
|
|
задаются уравнениями |
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
е |
|
|
|
|
|
|
|
|
|
|
|
|
|
x = − |
z2 |
+ |
y2 |
|
(pq > 0) |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
p |
q |
|||||||
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Р |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 4.28 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
175
