
Жданов С.К Цветков И.В - Основы физических процессов в плазме и в плазменных установках (2000)
.pdf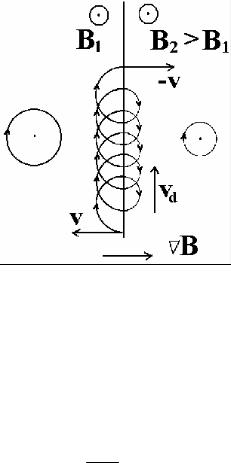
§16. Ⱦɪɟɣɮɡɚɪɹɠɟɧɧɵɯ ɱɚɫɬɢɰ ɜɞɨɥɶ ɩɥɨɫɤɨɫɬɢ ɫɤɚɱɤɚ ɦɚɝɧɢɬɧɨɝɨ ɩɨɥɹ
ȼɤɚɱɟɫɬɜɟ ɟɳɟ ɨɞɧɨɝɨ ɬɨɱɧɨ ɪɚɡɪɟɲɢɦɨɝɨ ɩɪɢɦɟɪɚ ɫ ɞɪɟɣɮɨɜɵɦ
ɞɜɢɠɟɧɢɟɦ ɪɚɫɫɦɨɬɪɢɦ ɡɚɞɚɱɭ ɨ ɞɜɢɠɟɧɢɢ ɡɚɪɹɠɟɧɧɨɣ ɱɚɫɬɢɰɵ ɜ ɦɚɝɧɢɬɧɨɦ ɩɨɥɟ ɫɨ ɫɤɚɱɤɨɦ, ɫɥɟɜɚ ɢ ɫɩɪɚɜɚ ɨɬ ɩɥɨɫɤɨɫɬɢ ɤɨɬɨɪɨɝɨ ɦɚɝɧɢɬɧɨɟ ɩɨɥɟ ɨɞɧɨɪɨɞɧɨ ɢ ɨɞɢɧɚɤɨɜɨ ɧɚɩɪɚɜɥɟɧɨ, ɧɨ ɢɦɟɟɬ ɪɚɡɧɭɸ ɜɟɥɢɱɢɧɭ (ɫɦ. ɪɢɫ. 2.3),
ɩɭɫɬɶ ɫɩɪɚɜɚ ɛɭɞɟɬ ȼ2>ȼ1. ȼɧɟ ɫɤɚɱɤɚ, ɝɞɟ ɩɨɥɟ ɨɞɧɨɪɨɞɧɨ, ɧɚ ɪɚɫɫɬɨɹɧɢɢ, ɩɪɟɜɵɲɚɸɳɟɦ ɥɚɪɦɨɪɨɜɫɤɢɣ ɪɚɞɢɭɫ, ɱɚɫɬɢɰɵ ɨɩɢɫɵɜɚɸɬ ɨɤɪɭɠɧɨɫɬɢ, ɪɚɡɦɟɪ ɤɨɬɨɪɵɯ ɛɨɥɶɲɟ ɜ ɨɛɥɚɫɬɢ ɫɥɚɛɨɝɨ ɩɨɥɹ (ɫɥɟɜɚ ɧɚ ɪɢɫ.2.3).
ɇɚ ɦɟɧɶɲɟɦ ɪɚɫɫɬɨɹɧɢɢ ɩɪɢ ɞɜɢɠɟɧɢɢ ɱɚɫɬɢɰɵ ɟɺ ɥɚɪɦɨɪɨɜɫɤɚɹ
ɨɤɪɭɠɧɨɫɬɶ ɩɟɪɟɫɟɤɚɟɬ ɩɥɨɫɤɨɫɬɶ ɫɤɚɱɤɚ, ɯɚɪɚɤɬɟɪ ɟɺ ɞɜɢɠɟɧɢɹ ɪɟɡɤɨ ɦɟɧɹɟɬɫɹ, ɬɚɤ
|
ɤɚɤ ɤɚɠɞɵɣ ɪɚɡ ɩɨɫɥɟ ɩɟɪɟɫɟɱɟɧɢɹ ɷɬɨɣ |
||||||||
|
ɩɥɨɫɤɨɫɬɢ |
ɫɤɚɱɤɨɦ |
ɢɡɦɟɧɹɟɬɫɹ |
ɪɚɞɢɭɫ |
|||||
|
ɨɤɪɭɠɧɨɫɬɢ. |
Ɍɪɚɟɤɬɨɪɢɹ |
ɩɪɢɨɛɪɟɬɚɟɬ |
||||||
|
ɫɥɨɠɧɵɣ |
|
ɯɚɪɚɤɬɟɪ |
|
ɫ |
ɧɚɥɢɱɢɟɦ |
|||
|
ɫɢɫɬɟɦɚɬɢɱɟɫɤɨɝɨ «ɫɧɨɫɚ» ɱɚɫɬɢɰɵ ɜɞɨɥɶ |
||||||||
|
ɩɥɨɫɤɨɫɬɢ ɫɤɚɱɤɚ. Ʉɚɤ ɜɢɞɧɨ ɢɡ ɪɢɫɭɧɤɚ, |
||||||||
|
ɞɪɟɣɮ |
ɩɟɪɩɟɧɞɢɤɭɥɹɪɟɧ |
|
ɧɚɩɪɚɜɥɟɧɢɸ |
|||||
|
ɦɚɝɧɢɬɧɨɝɨ ɩɨɥɹ ɢ ɟɝɨ ɝɪɚɞɢɟɧɬɚ, ɩɪɢɱɟɦ, |
||||||||
|
ɨɱɟɜɢɞɧɨ, ɢɦɟɟɬ ɩɪɨɬɢɜɨɩɨɥɨɠɧɵɣ ɡɧɚɤ ɞɥɹ |
||||||||
|
ɪɚɡɧɨɢɦɟɧɧɨ ɡɚɪɹɠɟɧɧɵɯ ɱɚɫɬɢɰ: ɞɥɹ |
||||||||
|
ɝɟɨɦɟɬɪɢɢ ɪɢɫ.2.3 ɨɧ ɧɚɩɪɚɜɥɟɧ ɜɜɟɪɯ ɞɥɹ |
||||||||
|
ɩɨɥɨɠɢɬɟɥɶɧɨɝɨ |
ɡɚɪɹɞɚ, |
ɢɥɢ |
ɛɵɥ |
ɛɵ |
||||
Ɋɢɫ.2.3. ɋɯɟɦɚ ɜɨɡɧɢɤɧɨɜɟɧɢɹ ɞɪɟɣɮɚ |
ɧɚɩɪɚɜɥɟɧ |
ɜɧɢɡ, |
ɟɫɥɢ |
ɛɵ |
ɡɚɪɹɞ |
ɛɵɥ |
|||
ɩɨɥɨɠɢɬɟɥɶɧɨɝɨ ɡɚɪɹɞɚ ɧɚ ɝɪɚɧɢɰɟ ɫɨ |
ɨɬɪɢɰɚɬɟɥɶɧɵɦ. |
|
|
|
|
|
|
||
ɫɤɚɱɤɨɦ ɜɟɥɢɱɢɧɵ ɦɚɝɧɢɬɧɨɝɨ ɩɨɥɹ |
ɇɟɬɪɭɞɧɨ ɩɨɞɫɱɢɬɚɬɶ ɫɤɨɪɨɫɬɶ ɷɬɨɝɨ |
||||||||
|
ɞɪɟɣɮɚ. |
ɉɭɫɬɶ |
ɞɥɹ |
ɩɪɨɫɬɨɬɵ |
ɱɚɫɬɢɰɚ |
||||
ɩɟɪɟɫɟɤɚɟɬ ɩɥɨɫɤɨɫɬɶ ɫɤɚɱɤɚ ɩɨ ɧɨɪɦɚɥɢ. Ɍɨɝɞɚ ɡɚ ɜɪɟɦɹ, ɪɚɜɧɨɟ ɫɭɦɦɟ ɥɚɪɦɨɪɨɜɫɤɢɯ ɩɨɥɭɩɟɪɢɨɞɨɜ ɞɥɹ ɨɛɥɚɫɬɢ ɫɥɟɜɚ ɢ ɫɩɪɚɜɚ
∆t = T |
+ T = |
π |
+ |
π |
|
, |
(2.23) |
|
ω 1 |
ω |
2 |
||||||
1 |
2 |
|
|
|
||||
|
|
|
|
|
|
ɝɞɟ
ω 1,2 = qBmc1,2 ,
ɰɢɤɥɨɬɪɨɧɧɵɟ ɱɚɫɬɨɬɵ, ɜɵɱɢɫɥɟɧɧɵɟ ɩɨ ɡɧɚɱɟɧɢɸ ɩɨɥɹ ɫɥɟɜɚ ɢ ɫɩɪɚɜɚ ɨɬ ɩɥɨɫɤɨɫɬɢ ɫɤɚɱɤɚ. ɑɚɫɬɢɰɚ ɫɦɟɳɚɟɬɫɹ ɜɞɨɥɶ ɷɬɨɣ ɩɥɨɫɤɨɫɬɢ ɧɚ ɞɥɢɧɭ
∆x = 2( ρ 1− ρ 2 ) = 2( |
v |
|
− |
v |
|
). |
(2.24) |
|
ω |
1 |
ω |
2 |
|||||
|
|
|
|
Ɂɞɟɫɶ v − ɫɤɨɪɨɫɬɶ ɱɚɫɬɢɰɵ, ɤɨɬɨɪɚɹ ɩɪɟɞɩɨɥɚɝɚɟɬɫɹ ɢɡɧɚɱɚɥɶɧɨ ɧɚɩɪɚɜɥɟɧɧɨɣ ɩɟɪɩɟɧɞɢɤɭɥɹɪɧɨ ɩɥɨɫɤɨɫɬɢ ɫɤɚɱɤɚ. Ɉɱɟɜɢɞɧɨ, ɫɤɨɪɨɫɬɶ ɞɪɟɣɮɚ ɦɨɠɧɨ ɨɩɪɟɞɟɥɢɬɶ ɤɚɤ
vd = |
∆x = |
2v |
|
B2 |
− B1 |
≡ |
v ∆B |
, |
(2.25) |
|||
|
|
|
|
|
|
|||||||
π |
B2 |
+ B1 |
π < B > |
|||||||||
|
∆t |
|
|
|
|
|||||||
ɝɞɟ ∆ȼ=ȼ2−ȼ1 − ɜɟɥɢɱɢɧɚ ɫɤɚɱɤɚ ɦɚɝɧɢɬɧɨɝɨ ɩɨɥɹ, ɚ <ȼ>=(ȼ2+ȼ1)/2 − ɟɝɨ ɫɪɟɞɧɟɟ ɡɧɚɱɟɧɢɟ. ɉɨɞɱɟɪɤɧɟɦ, ɱɬɨ ɩɨɥɭɱɟɧɧɨɟ ɪɟɲɟɧɢɟ − ɬɨɱɧɨɟ, ɩɪɢɱɟɦ ɜ ɭɫɥɨɜɢɹɯ, ɤɨɝɞɚ ɞɪɟɣɮɨɜɨɟ ɩɪɢɛɥɢɠɟɧɢɟ ɡɚɜɟɞɨɦɨ ɧɟɩɪɢɦɟɧɢɦɨ: ɪɚɡɦɟɪ
ɧɟɨɞɧɨɪɨɞɧɨɫɬɢ, ɤɚɤ ɩɪɟɞɩɨɥɚɝɚɟɬɫɹ, ɞɨɥɠɟɧ ɛɵɬɶ ɡɧɚɱɢɬɟɥɶɧɨ ɦɟɧɶɲɟ, ɱɟɦ ɥɚɪɦɨɪɨɜɫɤɢɟ ɪɚɞɢɭɫɵ ɱɚɫɬɢɰ!
ȼɟɥɢɱɢɧɚ ɫɤɨɪɨɫɬɢ ɞɪɟɣɮɚ ɡɚɜɢɫɢɬ, ɨɱɟɜɢɞɧɨ, ɢ ɨɬ ɭɝɥɚ, ɩɨɞ ɤɨɬɨɪɵɦ ɱɚɫɬɢɰɚ ɩɟɪɟɫɟɤɚɟɬ ɨɛɥɚɫɬɶ ɫɤɚɱɤɚ. Ɇɵ ɧɟ ɛɭɞɟɦ ɨɫɬɚɧɚɜɥɢɜɚɬɶɫɹ ɧɚ ɷɬɨɦ ɢɧɬɟɪɟɫɧɨɦ ɜɨɩɪɨɫɟ − ɷɬɭ ɡɚɜɢɫɢɦɨɫɬɶ ɧɟɫɥɨɠɧɨ ɩɨɥɭɱɢɬɶ, ɩɨ ɫɭɬɢ ɞɟɥɚ, ɬɟɦ ɠɟ ɫɚɦɵɦ ɩɭɬɟɦ, ɤɚɤ ɢ ɪɚɫɫɦɨɬɪɟɧɧɵɣ ɜɵɲɟ ɛɨɥɟɟ ɩɪɨɫɬɨɣ ɫɥɭɱɚɣ ɩɟɪɩɟɧɞɢɤɭɥɹɪɧɨɝɨ ɩɟɪɟɫɟɱɟɧɢɹ.
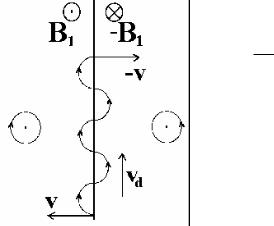
Ⱦɪɟɣɮ ɜɨɡɧɢɤɚɟɬ ɢ ɬɨɦ ɫɥɭɱɚɟ, ɤɨɝɞɚ ɫɥɟɜɚ ɢ ɫɩɪɚɜɚ ɨɬ ɧɟɤɨɬɨɪɨɣ ɩɥɨɫɤɨɫɬɢ ɦɚɝɧɢɬɧɨɟ ɩɨɥɟ ɩɨ ɜɟɥɢɱɢɧɟ ɧɟ ɦɟɧɹɟɬɫɹ, ɧɨ ɢɡɦɟɧɹɟɬ ɧɚɩɪɚɜɥɟɧɢɟ (ɫɦ. ɪɢɫ.2.4). Ɇɚɝɧɢɬɧɚɹ ɤɨɧɮɢɝɭɪɚɰɢɹ ɬɚɤɨɝɨ ɬɢɩɚ ɜɨɡɧɢɤɚɟɬ ɜ ɬɚɤ ɧɚɡɵɜɚɟɦɵɯ ɬɨɤɨɜɵɯ ɫɥɨɹɯ.
ȼ ɰɟɧɬɪɟ ɫɢɦɦɟɬɪɢɱɧɨɝɨ, ɧɚɩɪɢɦɟɪ, ɩɥɨɫɤɨɝɨ ɬɨɤɨɜɨɝɨ ɫɥɨɹ ɦɚɝɧɢɬɧɨɟ ɩɨɥɟ ɪɚɜɧɨ ɧɭɥɸ, ɚ ɜɧɟ ɷɬɨɣ ɰɟɧɬɪɚɥɶɧɨɣ ɩɥɨɫɤɨɫɬɢ, ɤɚɤ ɷɬɨ ɫɥɟɞɭɟɬ ɢɡ ɡɚɤɨɧɚ Ⱥɦɩɟɪɚ
& 4π &
rot B = c j , ɦɟɧɹɟɬ ɡɧɚɤ. ȿɫɥɢ ɬɨɥɳɢɧɨɣ ɫɥɨɹ
Ɋɢɫ.2.4. Ⱦɪɟɣɮ ɩɨɥɨɠɢɬɟɥɶɧɨɝɨ ɡɚɪɹɞɚ ɩɪɢ ɫɦɟɧɟ ɧɚɩɪɚɜɥɟɧɢɹ ɦɚɝɧɢɬɧɨɝɨ ɩɨɥɹ
ɫɤɨɪɨɫɬɶ ɞɪɟɣɮɚ ɞɥɹ ɷɬɨɝɨ ɫɥɭɱɚɹ:
vd = |
∆x |
= |
4ρ |
= |
4v / ω |
|
∆t |
T |
2π / ω |
||||
|
|
|
ɩɪɟɧɟɛɪɟɱɶ, ɩɨɥɭɱɢɦ ɫɤɚɱɨɤ ɧɚɩɪɚɜɥɟɧɢɹ ɩɨɥɹ.
ȼɧɟ ɫɥɨɹ ɱɚɫɬɢɰɵ ɜɪɚɳɚɸɬɫɹ ɩɨ ɥɚɪɦɨɪɨɜɫɤɢɦ ɨɤɪɭɠɧɨɫɬɹɦ, ɡɞɟɫɶ − ɨɞɢɧɚɤɨɜɨɝɨ ɪɚɞɢɭɫɚ, ɧɨ ɫ ɩɪɨɬɢɜɨɩɨɥɨɠɧɵɦ ɧɚɩɪɚɜɥɟɧɢɟɦ ɜɪɚɳɟɧɢɹ, ɢ ɞɪɟɣɮɚ ɧɟɬ, ɟɫɥɢ ɪɚɫɫɬɨɹɧɢɟ ɨɬ ɩɥɨɫɤɨɫɬɢ ɫɥɨɹ ɩɪɟɜɵɲɚɟɬ ɥɚɪɦɨɪɨɜɫɤɢɣ ɪɚɞɢɭɫ. Ⱦɪɟɣɮ ɜɨɡɧɢɤɚɟɬ, ɤɨɝɞɚ ɥɚɪɦɨɪɨɜɫɤɚɹ ɨɤɪɭɠɧɨɫɬɶ ɩɟɪɟɫɟɤɚɟɬ ɷɬɭ ɩɥɨɫɤɨɫɬɶ. Ɍɪɚɟɤɬɨɪɢɸ ɱɚɫɬɢɰɵ ɦɨɠɧɨ ɩɨɥɭɱɢɬɶ ɫɥɟɞɭɸɳɢɦ ɨɛɪɚɡɨɦ. ɉɭɫɬɶ ɩɟɪɟɫɟɱɟɧɢɟ ɩɥɨɫɤɨɫɬɢ ɫɥɨɹ ɱɚɫɬɢɰɟɣ – ɩɨ ɧɨɪɦɚɥɢ, ɬɨɝɞɚ ɥɚɪɦɨɪɨɜɫɤɭɸ ɨɤɪɭɠɧɨɫɬɶ ɫɥɟɞɭɟɬ «ɪɚɡɪɟɡɚɬɶ» ɜɞɨɥɶ ɜɟɪɬɢɤɚɥɶɧɨɝɨ ɞɢɚɦɟɬɪɚ ɢ ɡɚɬɟɦ, ɞɥɹ ɩɨɥɨɠɢɬɟɥɶɧɨɝɨ ɡɚɪɹɞɚ, ɩɪɚɜɭɸ ɩɨɥɨɜɢɧɭ ɫɥɟɞɭɟɬ ɨɬɪɚɡɢɬɶ ɡɟɪɤɚɥɶɧɨ ɜɜɟɪɯ, ɤɚɤ ɷɬɨ ɢɡɨɛɪɚɠɟɧɨ ɧɚ ɪɢɫ.2.4. ɉɪɢ ɷɬɨɦ ɡɚ ɥɚɪɦɨɪɨɜɫɤɢɣ ɩɟɪɢɨɞ ɫɦɟɳɟɧɢɟ ɜɞɨɥɶ ɫɥɨɹ, ɨɱɟɜɢɞɧɨ, ɫɨɫɬɚɜɥɹɟɬ ɞɜɚ ɥɚɪɦɨɪɨɜɫɤɢɯ ɞɢɚɦɟɬɪɚ, ɬɚɤ ɱɬɨ
= |
2 |
v . |
(2.26) |
|
|||
|
π |
|
|
ɉɪɢ ɩɟɪɟɫɟɱɟɧɢɢ «ɨɛɳɟɝɨ ɩɨɥɨɠɟɧɢɹ», ɩɪɢ ɩɪɨɢɡɜɨɥɶɧɨɦ ɭɝɥɟ, ɫɤɨɪɨɫɬɶ ɞɪɟɣɮɚ, ɨɱɟɜɢɞɧɨ, ɦɟɧɹɟɬɫɹ ɫ ɢɡɦɟɧɟɧɢɟɦ ɭɝɥɚ, ɧɨ ɧɟ ɡɚɜɢɫɢɬ ɨɬ ɜɟɥɢɱɢɧɵ ɦɚɝɧɢɬɧɨɝɨ ɩɨɥɹ! ɉɨɞɱɟɪɤɧɟɦ, ɱɬɨ ɢ ɜ ɷɬɨɦ ɫɥɭɱɚɟ ɞɪɟɣɮɨɜɨɟ ɩɪɢɛɥɢɠɟɧɢɟ ɧɟɩɪɢɦɟɧɢɦɨ.
§17. ȼɚɠɧɟɣɲɢɟ ɬɢɩɵ ɞɪɟɣɮɨɜɵɯ ɞɜɢɠɟɧɢɣ ɱɚɫɬɢɰ ɜ ɩɥɚɡɦɟ
Ɋɚɫɫɦɨɬɪɟɧɧɵɣ ɜ §15 ɩɪɢɦɟɪ ɞɜɢɠɟɧɢɹ ɱɚɫɬɢɰ ɜ ɦɚɝɧɢɬɧɨɦ ɩɨɥɟ ɩɨɞ ɞɟɣɫɬɜɢɟɦ ɞɨɩɨɥɧɢɬɟɥɶɧɨɣ ɩɨɫɬɨɹɧɧɨɣ ɫɢɥɵ ɹɜɥɹɟɬɫɹ ɬɨɱɧɵɦ ɪɟɲɟɧɢɟɦ ɧɟɪɟɥɹɬɢɜɢɫɬɫɤɢɯ ɭɪɚɜɧɟɧɢɣ ɞɜɢɠɟɧɢɹ. ȼɟɫɶɦɚ ɜɚɠɧɵɦ ɹɜɥɹɟɬɫɹ ɬɨ, ɱɬɨ ɡɚɤɨɧɨɦɟɪɧɨɫɬɢ, ɩɪɢɫɭɳɢɟ ɷɬɨɦɭ ɞɜɢɠɟɧɢɸ, ɫɨɯɪɚɧɹɸɬɫɹ ɢ ɜ ɫɥɭɱɚɟ, ɤɨɝɞɚ ɩɨɥɹ, ɞɟɣɫɬɜɭɸɳɢɟ ɧɚ ɱɚɫɬɢɰɭ, ɹɜɥɹɸɬɫɹ ɩɟɪɟɦɟɧɧɵɦɢ. Ɉɞɧɚɤɨ ɯɚɪɚɤɬɟɪɧɵɟ ɦɚɫɲɬɚɛɵ ɢɯ ɢɡɦɟɧɟɧɢɹ ɜɨ ɜɪɟɦɟɧɢ ɢ ɩɨ ɩɪɨɫɬɪɚɧɫɬɜɭ ɞɨɥɠɧɵ ɛɵɬɶ, ɤɚɤ ɭɠɟ ɨɛɫɭɠɞɚɥɨɫɶ, ɞɨɫɬɚɬɨɱɧɨ ɦɟɞɥɟɧɧɵɦɢ ɜ ɫɪɚɜɧɟɧɢɢ ɫ ɥɚɪɦɨɪɨɜɫɤɢɦ ɩɟɪɢɨɞɨɦ ɨɫɰɢɥɥɹɰɢɣ ɱɚɫɬɢɰɵ ɢ ɥɚɪɦɨɪɨɜɫɤɢɦ ɪɚɞɢɭɫɨɦ ɨɩɢɫɵɜɚɟɦɨɣ ɟɸ ɨɤɪɭɠɧɨɫɬɢ ɫɨɨɬɜɟɬɫɬɜɟɧɧɨ. ȼ ɷɬɨɦ ɫɥɭɱɚɟ ɞɥɹ ɫɤɨɪɨɫɬɢ ɞɪɟɣɮɚ ɜɧɨɜɶ ɫɩɪɚɜɟɞɥɢɜɚ ɮɨɪɦɭɥɚ (2.16). ɋ ɬɟɦ ɥɢɲɶ ɫɭɳɟɫɬɜɟɧɧɵɦ ɨɬɥɢɱɢɟɦ, ɱɬɨ ɫɤɨɪɨɫɬɶ ɞɪɟɣɮɚ ɞɨɥɠɧɚ ɛɵɬɶ ɞɨɫɬɚɬɨɱɧɚ ɦɚɥɚ, ɡɧɚɱɢɬɟɥɶɧɨ ɦɟɧɶɲɟ ɫɪɟɞɧɟɣ ɫɤɨɪɨɫɬɢ ɯɚɨɬɢɱɟɫɤɨɝɨ ɞɜɢɠɟɧɢɹ ɱɚɫɬɢɰ ɩɥɚɡɦɵ. ɉɨɫɥɟɞɧɹɹ, ɤɚɤ ɢɡɜɟɫɬɧɨ, ɨɩɪɟɞɟɥɹɟɬɫɹ ɬɟɩɥɨɜɨɣ ɫɤɨɪɨɫɬɶɸ ɱɚɫɬɢɰ. Ɍɚɤɢɦ ɨɛɪɚɡɨɦ, ɩɪɢɯɨɞɢɦ ɤ ɭɫɥɨɜɢɸ
vd << vT , |
(2.27) |
ɨɝɪɚɧɢɱɢɜɚɸɳɟɦɭ, ɩɪɢɱɟɦ ɡɚɱɚɫɬɭɸ ɜɟɫɶɦɚ ɫɭɳɟɫɬɜɟɧɧɨ, ɨɛɥɚɫɬɶ ɩɪɢɦɟɧɢɦɨɫɬɢ ɞɪɟɣɮɨɜɨɝɨ ɩɪɢɛɥɢɠɟɧɢɹ ɜ ɨɩɢɫɚɧɢɢ ɞɜɢɠɟɧɢɹ ɱɚɫɬɢɰ ɩɥɚɡɦɵ. ɉɪɟɞɩɨɥɚɝɚɹ ɭɤɚɡɚɧɧɵɟ ɨɝɪɚɧɢɱɟɧɢɹ ɜɵɩɨɥɧɟɧɧɵɦɢ, ɪɚɫɫɦɨɬɪɢɦ ɤɪɚɬɤɨ ɧɟɤɨɬɨɪɵɟ ɩɪɢɦɟɪɵ ɞɪɟɣɮɨɜɵɯ ɞɜɢɠɟɧɢɣ ɩɥɚɡɦɵ.
Ⱦɪɟɣɮ ɜ ɷɥɟɤɬɪɢɱɟɫɤɨɦ ɩɨɥɟ |
|
|
|
||||
ɉɪɢɪɨɞɚ ɫɢɥɵ F& |
ɦɨɠɟɬ ɛɵɬɶ ɥɸɛɨɣ, ɧɚɩɪɢɦɟɪ |
ɝɪɚɜɢɬɚɰɢɨɧɧɨɣ ɢɥɢ |
|||||
ɷɥɟɤɬɪɢɱɟɫɤɨɣ. ȼ ɱɚɫɬɧɨɦ ɫɥɭɱɚɟ ɷɥɟɤɬɪɢɱɟɫɤɨɣ ɩɪɢɪɨɞɵ ɫɢɥɵ, |
ɤɨɝɞɚ F& |
= eE& |
, ɩɨɥɭɱɢɦ |
||||
ɞɪɟɣɮ ɜ ɷɥɟɤɬɪɢɱɟɫɤɨɦ ɩɨɥɟ |
|
|
|
|
|||
v& |
= c |
E& × B& |
. |
|
|
|
(2.28) |
|
|
|
|
||||
E |
|
B2 |
|
|
|
|
|
Ⱦɪɟɣɮ ɜ ɷɥɟɤɬɪɢɱɟɫɤɨɦ ɩɨɥɟ ɧɟ ɡɚɜɢɫɢɬ ɨɬ ɡɧɚɤɚ ɡɚɪɹɞɚ - ɩɥɚɡɦɚ ɞɪɟɣɮɭɟɬ ɤɚɤ
ɰɟɥɨɟ.
Ɍɟɩɟɪɶ ɫɬɚɧɨɜɢɬɫɹ ɩɨɧɹɬɧɵɦ ɫɦɵɫɥ ɨɝɪɚɧɢɱɟɧɢɹ (2.11), ɧɚɥɨɠɟɧɧɨɝɨ ɧɚ ɡɧɚɱɟɧɢɟ ɜɟɥɢɱɢɧɵ ɷɥɟɤɬɪɢɱɟɫɤɨɝɨ ɩɨɥɹ. ɇɟɨɛɯɨɞɢɦɨ, ɱɬɨɛɵ ɫɤɨɪɨɫɬɶ ɞɪɟɣɮɚ ɩɨɞ ɞɟɣɫɬɜɢɟɦ ɷɥɟɤɬɪɢɱɟɫɤɨɝɨ ɩɨɥɹ ɛɵɥɚ ɡɧɚɱɢɬɟɥɶɧɨ ɦɟɧɶɲɟ ɬɟɩɥɨɜɨɣ ɫɤɨɪɨɫɬɢ ɱɚɫɬɢɰɵ, ɜ ɩɪɨɬɢɜɧɨɦ ɫɥɭɱɚɟ ɧɟɥɶɡɹ ɝɨɜɨɪɢɬɶ ɨ ɦɟɞɥɟɧɧɨɦ ɞɜɢɠɟɧɢɢ ɜɟɞɭɳɟɝɨ ɰɟɧɬɪɚ. ɋɭɳɟɫɬɜɟɧɧɨ, ɱɬɨ ɯɚɪɚɤɬɟɪ ɞɜɢɠɟɧɢɹ ɱɚɫɬɢɰɵ ɨɩɪɟɞɟɥɹɟɬɫɹ ɢɦɟɧɧɨ ɫɨɨɬɧɨɲɟɧɢɟɦ ɜɟɥɢɱɢɧ ɩɨɥɟɣ ȿ ɢ ȼ: ɩɪɢ ɛɨɥɶɲɢɯ ɡɧɚɱɟɧɢɹɯ ɩɨɥɹ ȿ ɜɥɢɹɧɢɟɦ ɩɨɥɹ ȼ ɦɨɠɧɨ ɩɪɟɧɟɛɪɟɱɶ, ɢ, ɨɱɟɜɢɞɧɨ, ɧɟ ɦɨɠɟɬ ɢɞɬɢ ɪɟɱɢ ɨ ɞɪɟɣɮɟ. ɉɪɢ ɦɚɥɵɯ ɡɧɚɱɟɧɢɹɯ ɷɥɟɤɬɪɢɱɟɫɤɨɝɨ ɩɨɥɹ ɩɨ ɫɪɚɜɧɟɧɢɸ ɫ ɦɚɝɧɢɬɧɵɦ ɱɚɫɬɢɰɚ "ɡɚɦɚɝɧɢɱɟɧɚ" ɢ ɦɟɞɥɟɧɧɨ ɞɪɟɣɮɭɟɬ ɜ ɦɚɝɧɢɬɧɨɦ ɩɨɥɟ ɩɨɞ ɞɟɣɫɬɜɢɟɦ ɷɥɟɤɬɪɢɱɟɫɤɨɝɨ ɩɨɥɹ.
Ⱦɪɟɣɮ ɜ ɧɟɨɞɧɨɪɨɞɧɨɦ ɦɚɝɧɢɬɧɨɦ ɩɨɥɟ ( B ≠0)
Ⱦɪɟɣɮ ɜ ɧɟɨɞɧɨɪɨɞɧɨɦ ɦɚɝɧɢɬɧɨɦ ɩɨɥɟ ɫɜɹɡɚɧ ɫ ɤɪɢɜɢɡɧɨɣ ɦɚɝɧɢɬɧɵɯ ɫɢɥɨɜɵɯ ɥɢɧɢɣ ɢ ɫ ɫɢɥɨɣ, ɜɨɡɧɢɤɚɸɳɟɣ ɩɪɢ ɞɜɢɠɟɧɢɢ ɱɚɫɬɢɰɵ ɜɞɨɥɶ ɤɪɢɜɨɥɢɧɟɣɧɵɯ ɫɢɥɨɜɵɯ ɥɢɧɢɣ. Ɋɚɫɫɦɨɬɪɢɦ ɞɜɟ ɫɨɫɬɚɜɥɹɸɳɢɟ ɷɬɨɣ ɫɢɥɵ ɢ ɫɨɨɬɜɟɬɫɬɜɟɧɧɨ ɩɨɥɭɱɢɦ ɞɜɟ ɫɨɫɬɚɜɥɹɸɳɢɟ ɞɪɟɣɮɚ.
•ɐɟɧɬɪɨɛɟɠɧɵɣ ɞɪɟɣɮ. ɉɪɢ ɞɜɢɠɟɧɢɢ ɱɚɫɬɢɰɵ, ɧɚɜɢɜɚɸɳɟɣɫɹ ɧɚ ɫɢɥɨɜɭɸ ɥɢɧɢɸ ɫ ɪɚɞɢɭɫɨɦ ɤɪɢɜɢɡɧɵ R, ɧɚ ɧɟɟ ɞɟɣɫɬɜɭɟɬ ɰɟɧɬɪɨɛɟɠɧɚɹ ɫɢɥɚ ɢɧɟɪɰɢɢ
& |
|
|
|
mv2 |
& |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|| |
|
|
|
|
|
|
|
|
|
|
|
F |
= − |
|
n , |
|
|
|
|
|
|
|
|
|
(2.29) |
||
|
|
|
|
|
|
|
|
|
|
||||||
ɰɛ |
|
|
|
R |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ɢ ɜɨɡɧɢɤɚɟɬ ɞɪɟɣɮɨɜɚɹ ɫɤɨɪɨɫɬɶ, ɪɚɜɧɚɹ ɩɨ ɜɟɥɢɱɢɧɟ |
|
||||||||||||||
vɰɛ |
= |
c mv||2 |
= |
v||2 |
1 |
= |
v||2 | B| |
, |
(2.30) |
||||||
|
|
|
|
|
|
|
|
|
|
||||||
e RB |
ω |
|
R |
ω |
|
B |
|||||||||
|
|
|
|
|
|
|
|
||||||||
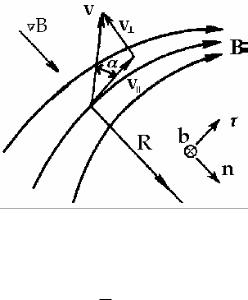
ɢ ɧɚɩɪɚɜɥɟɧɧɚɹ ɩɨ ɛɢɧɨɪɦɚɥɢ (ɡɚ ɩɥɨɫɤɨɫɬɶ ɪɢɫɭɧɤɚ, ɫɦ. ɪɢɫ. 2.5):
v&ɰɛ = |
v||2 |
|
[ B& B ] |
, |
(2.31) |
ω |
|
B2 |
ɝɞɟ vɰɛ - ɫɤɨɪɨɫɬɶ ɰɟɧɬɪɨɛɟɠɧɨɝɨ ɞɪɟɣɮɚ, ɚ ω − ɰɢɤɥɨɬɪɨɧɧɚɹ ɱɚɫɬɨɬɚ.
Ɋɢɫ. 2.5. Ⱦɪɟɣɮ ɜ ɧɟɨɞɧɨɪɨɞɧɨɦ ɦɚɝɧɢɬɧɨɦ ɩɨɥɟ
B = n& ,
B R
•Ƚɪɚɞɢɟɧɬɧɵɣ ɞɪɟɣɮ. ɋɤɨɪɨɫɬɶ ɞɪɟɣɮɚ ɜ
ɧɟɨɞɧɨɪɨɞɧɨɦ ɩɨɥɟ ɡɚɜɢɫɢɬ ɬɚɤɠɟ ɨɬ ɫɨɫɬɚɜɥɹɸɳɟɣ ɫɤɨɪɨɫɬɢ ɱɚɫɬɢɰɵ, ɩɟɪɩɟɧɞɢɤɭɥɹɪɧɨɣ ɤ ɦɚɝɧɢɬɧɨɦɭ ɩɨɥɸ. ɍɩɨɞɨɛɢɦ ɜɪɚɳɚɸɳɭɸɫɹ ɜɨɤɪɭɝ ɫɢɥɨɜɨɣ ɥɢɧɢɢ
ɱɚɫɬɢɰɭ ɦɚɝɧɢɬɧɨɦɭ ɞɢɩɨɥɸ ɷɤɜɢɜɚɥɟɧɬɧɨɝɨ ɤɪɭɝɨɜɨɝɨ ɬɨɤɚ. Ɍɨɝɞɚ ɬɨɱɧɨɟ ɜɵɪɚɠɟɧɢɟ
ɫɤɨɪɨɫɬɢ ɝɪɚɞɢɟɧɬɧɨɝɨ ɞɪɟɣɮɚ ɦɨɠɧɨ ɩɨɥɭɱɢɬɶ ɢɡ ɢɡɜɟɫɬɧɨɝɨ ɜɵɪɚɠɟɧɢɹ ɞɥɹ ɫɢɥɵ, ɞɟɣɫɬɜɭɸɳɟɣ
ɧɚ ɦɚɝɧɢɬɧɵɣ& ɞɢɩɨɥɶ ɜ ɧɟɨɞɧɨɪɨɞɧɨɦ ɩɨɥɟ:
F = − B . (2.32)
Ⱦɥɹ ɜɚɤɭɭɦɧɨɝɨ ɦɚɝɧɢɬɧɨɝɨ ɩɨɥɹ, ɤɚɤ ɦɨɠɧɨ ɩɨɤɚɡɚɬɶ, ɫɩɪɚɜɟɞɥɢɜɨ ɫɨɨɬɧɨɲɟɧɢɟ:
(2.33)
ɝɞɟ R, ɧɚɩɨɦɧɢɦ, - ɪɚɞɢɭɫ ɤɪɢɜɢɡɧɵ ɫɢɥɨɜɨɣ ɥɢɧɢɢ. ɉɨɷɬɨɦɭ ɩɨɩɟɪɟɱɧɚɹ ɤɨɦɩɨɧɟɧɬɚ ɫɢɥɵ, ɞɟɣɫɬɜɭɸɳɟɣ ɧɚ ɞɢɩɨɥɶ, ɨɤɚɡɵɜɚɟɬɫɹ ɪɚɜɧɨɣ
& |
|
|
|
B & |
|||
F |
= −µ |
|
|
|
n , |
||
|
R |
||||||
ɝɞɟ n& - ɟɞɢɧɢɱɧɵɣ ɜɟɤɬɨɪ ɧɨɪɦɚɥɢ. |
|||||||
ɉɨɞɫɬɚɜɥɹɹ ɷɬɨ ɡɧɚɱɟɧɢɟ F& ɜ ɜɵɪɚɠɟɧɢɟ (2.16), ɩɨɥɭɱɚɟɦ |
|||||||
v& |
= |
v2 |
|
[ B& B ] |
. |
||
|
|
||||||
ɝɪ |
|
2ω |
|
|
|
B2 |
|
(2.34)
(2.35)
Ɋɟɚɥɶɧɨ ɦɟɯɚɧɢɡɦ ɝɪɚɞɢɟɧɬɧɨɝɨ ɞɪɟɣɮɚ ɫɨɫɬɨɢɬ ɜ ɬɨɦ, ɱɬɨ ɱɚɫɬɢɰɚ ɢɦɟɟɬ ɪɚɡɥɢɱɧɵɟ ɪɚɞɢɭɫɵ ɜɪɚɳɟɧɢɹ ɜ ɪɚɡɧɵɯ ɬɨɱɤɚɯ ɬɪɚɟɤɬɨɪɢɢ: ɱɚɫɬɶ ɜɪɟɦɟɧɢ ɨɧɚ ɩɪɨɜɨɞɢɬ ɜ ɛɨɥɟɟ ɫɢɥɶɧɨɦ ɩɨɥɟ, ɱɚɫɬɶ ɜ ɛɨɥɟɟ ɫɥɚɛɨɦ ɩɨɥɟ. ɂɡɦɟɧɟɧɢɟ ɪɚɞɢɭɫɚ ɢ ɫɨɡɞɚɟɬ ɞɪɟɣɮ, ɤɚɤ ɷɬɨ ɨɛɫɭɠɞɚɥɢ ɜ ɩɪɟɞɵɞɭɳɟɦ ɩɚɪɚɝɪɚɮɟ.
ɋɤɨɪɨɫɬɶ ɞɪɟɣɮɚ ɜ ɧɟɨɞɧɨɪɨɞɧɨɦ ɦɚɝɧɢɬɧɨɦ ɩɨɥɟ ɩɪɟɞɫɬɚɜɥɹɟɬ ɫɨɛɨɣ ɫɭɦɦɭ ɫɤɨɪɨɫɬɟɣ ɰɟɧɬɪɨɛɟɠɧɨɝɨ ɢ ɝɪɚɞɢɟɧɬɧɨɝɨ ɞɪɟɣɮɨɜ (ɬɚɤ ɧɚɡɵɜɚɟɦɵɣ ɞɪɟɣɮ ɩɨ ɛɢɧɨɪɦɚɥɢ):
& |
2v||2 + v2 [ B& B ] |
|
1 |
2 |
2 |
& |
|
||
v b = |
|
|
|
= |
|
( v + 2v|| |
)b , |
(2.36) |
|
2ω |
B2 |
2ω R |
|||||||
ɝɞɟ b — ɨɪɬ ɛɢɧɨɪɦɚɥɢ (ɫɦ.ɪɢɫ.2.5).
ɋɤɨɪɨɫɬɶ ɞɪɟɣɮɚ ɡɚɜɢɫɢɬ ɨɬ ɡɚɪɹɞɚ ɱɚɫɬɢɰɵ (ɷɥɟɤɬɪɨɧɵ ɢ ɢɨɧɵ ɞɪɟɣɮɭɸɬ ɜ ɪɚɡɧɵɟ ɫɬɨɪɨɧɵ), ɨɬ ɟɺ ɦɚɫɫɵ, ɨɬ ɧɚɩɪɚɜɥɟɧɢɹ ɫɤɨɪɨɫɬɢ ɱɚɫɬɢɰɵ ɩɨ ɨɬɧɨɲɟɧɢɸ ɤ ɦɚɝɧɢɬɧɨɦɭ ɩɨɥɸ ɢ ɨɬ ɜɟɥɢɱɢɧ ɧɚɩɪɹɠɟɧɧɨɫɬɢ ɢ ɝɪɚɞɢɟɧɬɚ ɧɚɩɪɹɠɟɧɧɨɫɬɢ ɦɚɝɧɢɬɧɨɝɨ ɩɨɥɹ. ȼɚɠɧɨ
ɨɬɦɟɬɢɬɶ, ɱɬɨ ɬɪɚɟɤɬɨɪɢɹ ɜɟɞɭɳɟɝɨ ɰɟɧɬɪɚ ɩɪɨɯɨɞɢɬ ɜ ɨɛɥɚɫɬɢ ɩɨɫɬɨɹɧɧɨɝɨ ɡɧɚɱɟɧɢɹ ȼ, |
|||
& |
& |
& |
|
ɬɚɤ ɤɚɤ vb B ɢ |
vb B . |
|
|
ȼ ɧɟɨɞɧɨɪɨɞɧɨɦ ɦɚɝɧɢɬɧɨɦ ɩɨɥɟ ( B ≠ 0 ) ɷɥɟɤɬɪɨɧɵ ɢ ɢɨɧɵ ɞɪɟɣɮɭɸɬ ɜ ɪɚɡɧɵɟ |
|||
ɫɬɨɪɨɧɵ, ɫɥɟɞɨɜɚɬɟɥɶɧɨ, ɜ ɩɥɚɡɦɟ ɜɨɡɧɢɤɚɟɬ ɬɨɤ ɫ ɩɥɨɬɧɨɫɬɶɸ: |
|
||
j = ¦nev&b , |
(2.37) |
||
|
e,i |
|
|
ɝɞɟ ɩɪɟɞɩɨɥɚɝɚɟɬɫɹ ɫɭɦɦɢɪɨɜɚɧɢɟ ɩɨ ɫɨɪɬɚɦ ɡɚɪɹɠɟɧɧɵɯ ɱɚɫɬɢɰ. ɗɬɨɬ ɬɨɤ ɧɚɡɵɜɚɸɬ ɞɪɟɣɮɨɜɵɦ.
Ⱦɚɥɟɟ ɭɜɢɞɢɦ, ɱɬɨ ɝɪɚɞɢɟɧɬ ɞɚɜɥɟɧɢɹ ( p ≠ 0 ) ɬɚɤɠɟ ɩɪɢɜɨɞɢɬ ɤ ɩɨɹɜɥɟɧɢɸ ɞɪɟɣɮɨɜɵɯ ɬɨɤɨɜ.
ɉɨɥɹɪɢɡɚɰɢɨɧɧɵɣ ɞɪɟɣɮ
Ʉɨɝɞɚ ɱɚɫɬɢɰɚ ɢɫɩɵɬɵɜɚɟɬ& ɭɫɤɨɪɟɧɢɟ, ɬɨ ɜ ɞɜɢɠɭɳɟɣɫɹ ɫɢɫɬɟɦɟ ɤɨɨɪɞɢɧɚɬ ɧɚ ɧɟɟ ɞɟɣɫɬɜɭɟɬ ɢɧɟɪɰɢɨɧɧɚɹ ɫɢɥɚ F = −mv&, ɢ ɜɨɡɧɢɤɚɟɬ ɞɪɟɣɮ ɜ ɫɨɨɬɜɟɬɫɬɜɢɢ ɫ ɭɫɥɨɜɢɟɦ (2.17). ȼ ɩɥɚɡɦɟ ɱɚɫɬɨ ɩɨɹɜɥɹɸɬɫɹ ɩɟɪɟɦɟɧɧɵɟ ɷɥɟɤɬɪɢɱɟɫɤɢɟ ɩɨɥɹ, ɨɩɪɟɞɟɥɹɟɦɵɟ ɦɟɫɬɧɵɦ ɪɚɡɞɟɥɟɧɢɟɦ ɡɚɪɹɞɨɜ, ɬɚɤ ɧɚɡɵɜɚɟɦɵɟ ɩɨɥɹɪɢɡɚɰɢɨɧɧɵɟ ɩɨɥɹ. ȼ ɷɬɨɦ ɫɥɭɱɚɟ ɧɚ ɱɚɫɬɢɰɭ ɞɟɣɫɬɜɭɟɬ ɩɟɪɟɦɟɧɧɚɹ ɫɢɥɚ, ɢ ɜɨɡɧɢɤɚɟɬ ɷɥɟɤɬɪɢɱɟɫɤɢɣ ɞɪɟɣɮ ɫ ɩɟɪɟɦɟɧɧɨɣ ɫɤɨɪɨɫɬɶɸ
|
|
~ |
& |
|
|
|
~& |
E × B |
, |
|
|
|
vn = c |
B2 |
|
|
|
~ |
|
|
|
~ |
- ɫɨɫɬɚɜɥɹɸɳɚɹ ɷɥɟɤɬɪɢɱɟɫɤɨɝɨ ɩɨɥɹ, |
ɝɞɟ vn |
- ɞɪɟɣɮɨɜɚɹ ɩɨɥɹɪɢɡɚɰɢɨɧɧɚɹ ɫɤɨɪɨɫɬɶ; E |
||||
ɩɟɪɩɟɧɞɢɤɭɥɹɪɧɚɹ ɤ ɦɚɝɧɢɬɧɨɦɭ ɩɨɥɸ. ɂɦɟɧɧɨ ɨɧɚ ɢ ɜɵɡɵɜɚɟɬ ɞɪɟɣɮ. ɉɪɢ ɩɟɪɟɦɟɧɧɨɦ |
|||||||||
~ |
|
|
|
|
|
~ |
|
& |
& |
|
|
|
|
|
|
|
|
|
|
E ɦɟɧɹɟɬɫɹ ɢ vn , ɬ.ɟ. ɩɨɹɜɥɹɟɬɫɹ ɭɫɤɨɪɟɧɢɟ, ɚ, ɫɥɟɞɨɜɚɬɟɥɶɧɨ, ɢ ɫɢɥɚ ɢɧɟɪɰɢɢ Fu = −mvn . |
|||||||||
ɉɨɞ ɞɟɣɫɬɜɢɟɦ ɷɬɨɣ ɫɢɥɵ ɜɨɡɧɢɤɚɟɬ ɩɨɥɹɪɢɡɚɰɢɨɧɧɵɣ ɞɪɟɣɮ |
|
|
|||||||
|
|
c |
2 |
|
|
~ |
|
|
|
v& |
= |
|
|
mE |
. |
|
(2.38) |
||
e |
|
|
|||||||
n |
|
|
|
B2 |
|
|
|||
ȼɟɥɢɱɢɧɚ |
|
v&n |
|
|
ɡɚɜɢɫɢɬ ɨɬ ɦɚɫɫɵ (ɛɨɥɶɲɚɹ ɜɟɥɢɱɢɧɚ ɭ ɢɨɧɨɜ), ɡɚɪɹɞɚ ɱɚɫɬɢɰɵ, |
||||
ɧɚɩɪɹɠɟɧɧɨɫɬɢ |
ɦɚɝɧɢɬɧɨɝɨ ɩɨɥɹ ɢ ɫɤɨɪɨɫɬɢ & ɢɡɦɟɧɟɧɢɹ |
ɷɥɟɤɬɪɢɱɟɫɤɨɝɨ ɩɨɥɹ. |
|||||||
|
|
|
|
|
|
~ |
|
|
|
ɉɨɥɹɪɢɡɚɰɢɨɧɧɵɣ ɞɪɟɣɮ ɧɚɩɪɚɜɥɟɧ ɜɞɨɥɶ ɜɟɤɬɨɪɚE - ɩɟɪɩɟɧɞɢɤɭɥɹɪɧɨɣ ɫɨɫɬɚɜɥɹɸɳɟɣ |
|||||||||
ɩɪɨɢɡɜɨɞɧɨɣ ɩɨ ɜɪɟɦɟɧɢ ɨɬ ɧɚɩɪɹɠɟɧɧɨɫɬɢ ɷɥɟɤɬɪɢɱɟɫɤɨɝɨ ɩɨɥɹ - ɩɚɪɚɥɥɟɥɶɧɨ ɢɥɢ ɚɧɬɢɩɚɪɚɥɥɟɥɶɧɨ ɟɦɭ.
ɗɬɨɬ ɞɪɟɣɮ ɫɨɡɞɚɟɬ ɩɨɥɹɪɢɡɚɰɢɨɧɧɵɣ ɬɨɤ - ɚɧɚɥɨɝ ɬɨɤɚ ɫɦɟɳɟɧɢɹ:
& |
|
|
|
c2 |
& |
|
|
|
|
|
|
|
|
jn = nev&n = ρm |
|
E , |
|
|
|
|
(2.39) |
||||||
B2 |
|
|
|
|
|||||||||
ɝɞɟ ρm - ɦɚɫɫɨɜɚɹ ɩɥɨɬɧɨɫɬɶ ɩɥɚɡɦɵ. |
|
|
|
|
|
|
|||||||
Ɇɨɠɧɨ ɨɩɪɟɞɟɥɢɬɶ ɢ ɫɨɫɬɚɜɥɹɸɳɭɸ ε |
ɞɢɷɥɟɤɬɪɢɱɟɫɤɨɣ ɩɨɫɬɨɹɧɧɨɣ |
ɩɥɚɡɦɵ, |
|||||||||||
ɩɟɪɩɟɧɞɢɤɭɥɹɪɧɭɸ |
ɤ |
ɦɚɝɧɢɬɧɨɦɭ |
ɩɨɥɸ. |
Ⱦɨɛɚɜɥɹɹ ɤ ɩɨɥɹɪɢɡɚɰɢɨɧɧɨɦɭ ɬɨɤɭ |
&jn |
||||||||
|
|
|
|
|
|
|
|
|
& |
1 |
& |
|
|
ɩɨɩɟɪɟɱɧɭɸ |
ɤɨɦɩɨɧɟɧɬɭ ɬɨɤɚ ɫɦɟɳɟɧɢɹ |
jɫɦ = |
4π |
E (ɡɞɟɫɶ ɬɨɱɤɨɣ ɨɬɦɟɱɟɧɚ |
ɱɚɫɬɧɚɹ |
||||||||
ɩɪɨɢɡɜɨɞɧɚɹ ɨɬ ɩɨɥɹ ɩɨ ɜɪɟɦɟɧɢ), ɩɨɥɭɱɢɦ |
|
|
|
|
|
||||||||
& |
& |
& |
1 |
|
|
c2 |
& |
|
|
|
|
|
|
j = |
jɩ |
+ jɫɦ = |
4π |
(1 + 4π ρm B2 )E . |
|
|
|
(2.40) |
|||||
ɍɱɢɬɵɜɚɹ ɞɚɥɟɟ, ɱɬɨ ɩɥɨɬɧɨɫɬɶ ɬɨɤɚ ɫɜɹɡɚɧɚ ɫ ɩɪɨɢɡɜɨɞɧɨɣ ɩɨɥɹ ɩɨ ɜɪɟɦɟɧɢ ɯɨɪɨɲɨ ɢɡɜɟɫɬɧɵɦ ɫɨɨɬɧɨɲɟɧɢɟɦ
& |
|
|
ε |
& |
|
|
|
|
j |
= |
4π |
E , |
|
|
(2.41) |
||
ɧɚɯɨɞɢɦ |
|
|
|
|
|
|
|
|
ε |
|
= 1 + 4πρ |
c2 |
. |
(2.42) |
|||
|
||||||||
|
|
|
m B2 |
|
|
|||
Ɍɨɪɨɢɞɚɥɶɧɵɣ ɞɪɟɣɮ ɢ ɜɪɚɳɚɬɟɥɶɧɨɟ ɩɪɟɨɛɪɚɡɨɜɚɧɢɟ
Ɋɚɫɫɦɨɬɪɢɦ ɩɨɜɟɞɟɧɢɟ ɩɥɚɡɦɵ ɜ ɦɚɝɧɢɬɧɨɦ ɩɨɥɟ ɬɨɪɨɢɞɚɥɶɧɨɝɨ ɫɨɥɟɧɨɢɞɚ. Ɇɚɝɧɢɬɧɨɟ ɩɨɥɟ ɬɨɪɨɢɞɚɥɶɧɨɝɨ ɫɨɥɟɧɨɢɞɚ ɚɧɚɥɨɝɢɱɧɨ ɦɚɝɧɢɬɧɨɦɭ ɩɨɥɸ ɩɪɹɦɨɝɨ ɩɪɨɜɨɞɧɢɤɚ ɢ ɭɛɵɜɚɟɬ ɫ ɭɜɟɥɢɱɟɧɢɟɦ ɛɨɥɶɲɨɝɨ ɪɚɞɢɭɫɚ ɩɨ ɡɚɤɨɧɭ 1/R (ɪɢɫ.2.6). ɗɬɨ ɫɬɚɧɨɜɢɬɫɹ ɨɱɟɜɢɞɧɵɦ, ɟɫɥɢ ɭɱɟɫɬɶ, ɱɬɨ ɜɟɥɢɱɢɧɚ ɬɨɤɚ ɧɚ ɟɞɢɧɢɰɭ ɞɥɢɧɵ ɨɤɪɭɠɧɨɫɬɢ

2π(R-r) ɛɨɥɶɲɟ, ɱɟɦ ɫɨɨɬɜɟɬɫɬɜɭɸɳɚɹ ɜɟɥɢɱɢɧɚ ɧɚ ɨɤɪɭɠɧɨɫɬɢ 2π(R+r), ɝɞɟ r - ɪɚɞɢɭɫ ɩɨɩɟɪɟɱɧɨɝɨ ɫɟɱɟɧɢɹ ɬɨɪɚ (ɫɦ. ɪɢɫ.2.6). ɇɟɨɞɧɨɪɨɞɧɨɫɬɶ ɦɚɝɧɢɬɧɨɝɨ ɩɨɥɹ ɜɵɡɵɜɚɟɬ ɜɨɡɧɢɤɧɨɜɟɧɢɟ ɞɪɟɣɮɚ, ɩɪɢɜɨɞɹɳɟɝɨ ɤ ɫɦɟɳɟɧɢɸ ɢɨɧɨɜ ɧɚ ɨɞɧɭ (ɧɚ ɪɢɫ.2.6 - ɜɧɢɡ), ɚ ɷɥɟɤɬɪɨɧɨɜ ɧɚ ɞɪɭɝɭɸ (ɧɚ ɪɢɫ.2.6 - ɜɜɟɪɯ) ɫɬɨɪɨɧɭ ɫɨɥɟɧɨɢɞɚ, ɚ, ɡɧɚɱɢɬ, ɤ ɩɨɹɜɥɟɧɢɸ ɞɪɟɣɮɨɜɨɝɨ ɬɨɤɚ. Ɍɚɤ ɤɚɤ ɞɪɟɣɮɨɜɵɣ ɬɨɤ ɡɚɦɤɧɭɬɶɫɹ ɧɟ ɦɨɠɟɬ, ɬɨ ɜɨɡɧɢɤɚɟɬ ɪɚɡɞɟɥɟɧɢɟ ɡɚɪɹɞɨɜ ɢ ɫɨɨɬɜɟɬɫɬɜɭɸɳɟɟ ɟɦɭ ɩɨɥɹɪɢɡɚɰɢɨɧɧɨɟ ɷɥɟɤɬɪɢɱɟɫɤɨɟ ɩɨɥɟ ȿ.
ɇɨ ɬɟɩɟɪɶ ɩɨɹɜɥɟɧɢɟ ɷɬɨɝɨ ɩɨɥɹ ɩɪɢɜɨɞɢɬ ɤ ɜɨɡɧɢɤɧɨɜɟɧɢɸ ɞɪɟɣɮɚ ɩɥɚɡɦɵ ɜ ɰɟɥɨɦ ɜ ɫɤɪɟɳɟɧɧɵɯ ɜɡɚɢɦɧɨ ɩɟɪɩɟɧɞɢɤɭɥɹɪɧɵɯ ȿ ȼ ɩɨɥɹɯ, ɜɵɛɪɚɫɵɜɚɸɳɟɝɨ ɩɥɚɡɦɭ ɧɚ ɧɚɪɭɠɧɭɸ ɫɬɟɧɤɭ ɬɨɪɨɢɞɚɥɶɧɨɝɨ ɫɨɥɟɧɨɢɞɚ.
|
Ɍɚɤɢɦ ɨɛɪɚɡɨɦ, ɜ ɫɜɨɛɨɞɧɨɦ ɨɬ ɜɧɭɬɪɟɧɧɢɯ |
|
|
ɬɨɤɨɜ ɬɨɪɨɢɞɚɥɶɧɨɦ ɫɨɥɟɧɨɢɞɟ ɩɥɚɡɦɚ ɧɟ ɛɭɞɟɬ |
|
|
ɭɫɬɨɣɱɢɜɨ ɭɞɟɪɠɢɜɚɬɶɫɹ. Ʉɚɪɬɢɧɚ ɩɪɢɧɰɢɩɢɚɥɶɧɨ |
|
|
ɢɡɦɟɧɢɬɫɹ, ɟɫɥɢ ɜɧɭɬɪɢ, ɜ ɰɟɧɬɪɟ ɫɟɱɟɧɢɹ |
|
|
ɫɨɥɟɧɨɢɞɚ, ɩɨɦɟɫɬɢɬɶ ɩɪɨɜɨɞɧɢɤ ɫ ɬɨɤɨɦ, ɢɥɢ |
|
|
ɩɪɨɩɭɫɬɢɬɶ ɬɨɤ ɧɟɩɨɫɪɟɞɫɬɜɟɧɧɨ ɩɨ ɩɥɚɡɦɟ. ɗɬɨɬ |
|
|
ɬɨɤ ɫɨɡɞɚɫɬ ɫɨɛɫɬɜɟɧɧɨɟ ɦɚɝɧɢɬɧɨɟ ɩɨɥɟ ȼϕ, |
|
Ɋɢɫ. 2.6. Ɍɨɪɨɢɞɚɥɶɧɵɣ ɞɪɟɣɮ. |
ɩɟɪɩɟɧɞɢɤɭɥɹɪɧɨɟ ɤ ɩɨɥɸ ɫɨɥɟɧɨɢɞɚ ȼz, ɬɚɤ ɱɬɨ |
|
ɫɭɦɦɚɪɧɚɹ ɫɢɥɨɜɚɹ ɥɢɧɢɹ ɦɚɝɧɢɬɧɨɝɨ ɩɨɥɹ ɩɨɣɞɟɬ |
||
|
ɩɨ ɜɢɧɬɨɜɨɣ ɬɪɚɟɤɬɨɪɢɢ, ɨɯɜɚɬɵɜɚɸɳɟɣ ɨɫɶ ɫɨɥɟɧɨɢɞɚ. Ɉɛɪɚɡɨɜɚɧɢɟ ɜɢɧɬɨɜɵɯ ɥɢɧɢɣ ɦɚɝɧɢɬɧɨɝɨ ɩɨɥɹ ɩɨɥɭɱɢɥɨ ɧɚɡɜɚɧɢɟ
ɜɪɚɳɚɬɟɥɶɧɨɝɨ (ɢɥɢ ɪɨɬɚɰɢɨɧɧɨɝɨ) ɩɪɟɨɛɪɚɡɨɜɚɧɢɹ. ɗɬɢ ɥɢɧɢɢ ɛɭɞɭɬ ɡɚɦɵɤɚɬɶɫɹ ɫɚɦɢ ɧɚ ɫɟɛɹ, ɟɫɥɢ ɤɨɷɮɮɢɰɢɟɧɬ ɡɚɩɚɫɚ ɭɫɬɨɣɱɢɜɨɫɬɢ, ɩɪɟɞɫɬɚɜɥɹɸɳɢɣ ɫɨɛɨɣ ɨɬɧɨɲɟɧɢɟ ɲɚɝɚ
ɜɢɧɬɨɜɨɣ ɫɢɥɨɜɨɣ ɥɢɧɢɢ ɤ ɞɥɢɧɟ ɨɫɢ ɬɨɪɚ |
|
||||
q = |
Bz |
|
a |
, |
(2.43) |
B |
|
R |
|||
|
|
|
|
||
|
ϕ |
|
|
|
|
ɛɭɞɟɬ ɪɚɜɟɧ ɨɬɧɨɲɟɧɢɸ ɞɜɭɯ ɰɟɥɵɯ ɱɢɫɟɥ, ɬ.ɟ. ɪɚɜɟɧ ɪɚɰɢɨɧɚɥɶɧɨɦɭ ɱɢɫɥɭ - ɨɬɧɨɲɟɧɢɸ ɱɢɫɥɚ ɨɛɨɪɨɬɨɜ ɫɢɥɨɜɨɣ ɥɢɧɢɢ ɜɨɤɪɭɝ ɬɨɪɚ ɢ ɱɢɫɥɚ ɨɛɨɪɨɬɨɜ ɜɨɤɪɭɝ ɨɫɢ ɬɨɪɚ. ɉɪɢ ɡɧɚɱɟɧɢɹɯ ɷɬɨɣ ɜɟɥɢɱɢɧɵ, ɧɟ ɪɚɜɧɵɯ ɪɚɰɢɨɧɚɥɶɧɨɦɭ ɱɢɫɥɭ, ɫɢɥɨɜɵɟ ɥɢɧɢɣ, ɧɢɤɨɝɞɚ ɧɟ ɡɚɦɵɤɚɹɫɶ, ɡɚ ɛɟɫɤɨɧɟɱɧɨɟ ɱɢɫɥɨ ɨɛɨɪɨɬɨɜ ɨɛɪɚɡɭɸɬ ɡɚɦɤɧɭɬɵɟ ɬɨɪɨɢɞɚɥɶɧɵɟ ɦɚɝɧɢɬɧɵɟ ɩɨɜɟɪɯɧɨɫɬɢ, ɜɥɨɠɟɧɧɵɟ ɞɪɭɝ ɜ ɞɪɭɝɚ ɢ ɨɛɪɚɡɨɜɚɧɧɵɟ ɤɚɠɞɚɹ ɟɞɢɧɫɬɜɟɧɧɨɣ ɫɢɥɨɜɨɣ ɥɢɧɢɟɣ. ȼɢɧɬɨɜɵɟ ɥɢɧɢɢ ɦɚɝɧɢɬɧɨɝɨ ɩɨɥɹ ɫɞɟɥɚɸɬ ɧɟɜɨɡɦɨɠɧɨɣ ɩɨɥɹɪɢɡɚɰɢɸ ɩɥɚɡɦɵ: ɩɟɪɟɦɟɳɚɹɫɶ ɜɞɨɥɶ ɧɢɯ, ɷɥɟɤɬɪɨɧɵ ɢ ɢɨɧɵ ɫɨɡɞɚɞɭɬ ɞɪɟɣɮɨɜɵɟ ɬɨɤɢ, ɤɨɬɨɪɵɟ ɛɭɞɭɬ
ɜɡɚɢɦɧɨ ɧɟɣɬɪɚɥɢɡɨɜɚɧɵ, ɧɟ ɛɭɞɟɬ ɪɚɡɞɟɥɟɧɢɹ ɡɚɪɹɞɨɜ, ɧɟ ɩɨɹɜɢɬɫɹ ɢ ɷɥɟɤɬɪɢɱɟɫɤɨɟ ɩɨɥɟ. ɋɥɟɞɨɜɚɬɟɥɶɧɨ, ɧɟ ɜɨɡɧɢɤɧɟɬ ɢ ɬɨɪɨɢɞɚɥɶɧɵɣ ɞɪɟɣɮ, ɜɵɛɪɚɫɵɜɚɸɳɢɣ ɩɥɚɡɦɭ ɧɚ ɧɚɪɭɠɧɭɸ ɫɬɟɧɤɭ, ɢɦɟɸɳɢɣ ɦɟɫɬɨ ɜ ɛɟɫɬɨɤɨɜɨɦ ɬɨɪɨɢɞɚɥɶɧɨɦ ɫɨɥɟɧɨɢɞɟ.
ɋɭɳɟɫɬɜɟɧɧɨ, ɱɬɨ ɜ ɤɚɠɞɨɣ ɬɨɱɤɟ ɫɜɨɟ ɫɨɨɬɧɨɲɟɧɢɟ ɜɟɥɢɱɢɧ ɦɚɝɧɢɬɧɵɯ ɩɨɥɟɣ ɬɨɤɚ ɢ ɫɨɥɟɧɨɢɞɚ (ɜɟɞɶ ɦɚɝɧɢɬɧɨɟ ɩɨɥɟ ɬɨɤɚ ɛɭɞɟɬ ɭɛɵɜɚɬɶ ɩɨ ɡɚɤɨɧɭ 1/r (r ɦɚɥɨɟ!) ɜɨ ɜɫɟ ɫɬɨɪɨɧɵ ɨɬ ɬɨɤɚ). ɉɨɷɬɨɦɭ ɫɢɥɨɜɵɟ ɥɢɧɢɢ ɪɚɫɩɨɥɨɠɟɧɧɵɯ ɪɹɞɨɦ ɦɚɝɧɢɬɧɵɯ ɩɨɜɟɪɯɧɨɫɬɟɣ ɫɤɪɟɳɢɜɚɸɬɫɹ, ɩɪɢɱɟɦ ɭɝɨɥ ɧɚɤɥɨɧɚ ɧɟɩɪɟɪɵɜɧɨ ɦɟɧɹɟɬɫɹ ɫ ɢɡɦɟɧɟɧɢɟɦ R. Ɉɛɪɚɡɭɟɬɫɹ ɫɥɨɠɧɚɹ ɩɪɨɫɬɪɚɧɫɬɜɟɧɧɚɹ ɫɟɬɤɚ ɦɚɝɧɢɬɧɵɯ ɫɢɥɨɜɵɯ ɥɢɧɢɣ, ɩɨɥɭɱɢɜɲɚɹ ɧɚɡɜɚɧɢɟ ɲɢɪ. Ɍɚɤɚɹ ɫɟɬɤɚ ɫɭɳɟɫɬɜɟɧɧɨ ɡɚɬɪɭɞɧɹɟɬ ɩɟɪɟɦɟɳɟɧɢɟ ɩɥɚɡɦɵ ɩɨɩɟɪɟɤ ɦɚɝɧɢɬɧɨɝɨ ɩɨɥɹ.
ȼ ɫɢɫɬɟɦɚɯ ɬɢɩɚ ɬɨɤɚɦɚɤ (ɫɨɤɪɚɳɟɧɧɨɟ ɨɬ «ɬɨɤɨɜɚɹ ɤɚɦɟɪɚ ɫ ɦɚɝɧɢɬɧɵɦɢ ɤɚɬɭɲɤɚɦɢ») ɜɧɭɬɪɢ ɬɨɪɨɢɞɚɥɶɧɨɝɨ ɫɨɥɟɧɨɢɞɚ ɩɨ ɩɥɚɡɦɟ ɬɟɱɟɬ ɬɨɤ, ɢɦɟɟɬɫɹ ɜɪɚɳɚɬɟɥɶɧɨɟ ɩɪɟɨɛɪɚɡɨɜɚɧɢɟ ɢ ɲɢɪ. Ʉɨɧɟɱɧɨ, ɬɨɤ ɪɚɫɩɪɟɞɟɥɟɧ ɩɨ ɫɟɱɟɧɢɸ ɩɥɚɡɦɟɧɧɨɝɨ ɲɧɭɪɚ (ɚ ɬɟɱɟɬ ɧɟ ɬɨɥɶɤɨ ɜ ɰɟɧɬɪɟ), ɡɧɚɱɢɬ, ɪɟɚɥɶɧɚɹ ɤɚɪɬɢɧɚ ɫɥɨɠɧɟɟ ɪɚɫɫɦɨɬɪɟɧɧɨɣ ɜɵɲɟ, ɧɨ ɜɨɡɦɨɠɧɨɫɬɶ ɤɨɦɩɟɧɫɚɰɢɢ ɷɮɮɟɤɬɚ ɬɨɪɨɢɞɚɥɶɧɨɝɨ ɞɪɟɣɮɚ ɨɫɬɚɟɬɫɹ ɜ ɫɢɥɟ.
Ⱥɦɟɪɢɤɚɧɫɤɢɣ ɮɢɡɢɤ ɋɩɢɬɰɟɪ ɞɨɤɚɡɚɥ, ɱɬɨ ɜɪɚɳɚɬɟɥɶɧɨɟ ɩɪɟɨɛɪɚɡɨɜɚɧɢɟ ɦɨɠɧɨ ɩɨɥɭɱɢɬɶ ɢ ɛɟɡ ɬɨɤɚ ɜ ɩɥɚɡɦɟ. Ɍɚɤɨɝɨ ɬɢɩɚ ɫɢɫɬɟɦɵ ɞɥɹ ɭɞɟɪɠɚɧɢɹ ɩɥɚɡɦɵ ɩɨɥɭɱɢɥɢ ɧɚɡɜɚɧɢɟ ɫɬɟɥɥɚɪɚɬɨɪɵ. ȼɨɡɦɨɠɧɨɫɬɶ ɪɟɚɥɢɡɚɰɢɢ ɜɪɚɳɚɬɟɥɶɧɨɝɨ ɩɪɟɨɛɪɚɡɨɜɚɧɢɹ ɛɟɡ ɬɨɤɚ ɜ ɩɥɚɡɦɟ ɦɨɠɧɨ ɩɨɹɫɧɢɬɶ ɫ ɩɨɦɨɳɶɸ ɫɯɟɦɵ, ɢɡɨɛɪɚɠɟɧɧɨɣ ɧɚ ɪɢɫ. 2.7.
Ɋɚɡɪɟɠɟɦ (ɦɵɫɥɟɧɧɨ) ɬɨɪɨɢɞɚɥɶɧɵɣ ɫɨɥɟɧɨɢɞ ɩɨɩɨɥɚɦ ɢ ɫɨɟɞɢɧɢɦ ɟɝɨ ɤɨɧɰɵ:
ɚ) ɩɪɹɦɨɥɢɧɟɣɧɵɦɢ ɭɱɚɫɬɤɚɦɢ – ɩɨɥɭɱɢɦ ɬɚɤ ɧɚɡɵɜɚɟɦɵɣ ɪɟɣɫɬɪɟɤ (ɜ ɩɪɹɦɵɯ ɭɱɚɫɬɤɚɯ ɬɨɠɟ ɫɨɡɞɚɟɬɫɹ ɦɚɝɧɢɬɧɨɟ ɩɨɥɟ). ɋɢɥɨɜɵɟ ɥɢɧɢɢ ɦɚɝɧɢɬɧɨɝɨ ɩɨɥɹ ɡɚɦɵɤɚɸɬɫɹ, ɞɪɟɣɮ ɡɚɪɹɠɟɧɧɵɯ ɱɚɫɬɢɰ ɜ ɩɪɚɜɨɣ ɢ ɥɟɜɨɣ ɬɨɪɨɢɞɚɥɶɧɵɯ ɱɚɫɬɹɯ ɢɦɟɟɬ ɨɞɢɧɚɤɨɜɨɟ ɧɚɩɪɚɜɥɟɧɢɟ. ɉɨɷɬɨɦɭ ɩɨ-ɩɪɟɠɧɟɦɭ ɨɫɬɚɟɬɫɹ ɜɨɡɦɨɠɧɨɫɬɶ ɜɨɡɧɢɤɧɨɜɟɧɢɹ ɩɨɥɹɪɢɡɚɰɢɨɧɧɨɝɨ ɷɥɟɤɬɪɢɱɟɫɤɨɝɨ ɩɨɥɹ ȿ ɢ ɞɪɟɣɮɚ ɜ ɩɟɪɩɟɧɞɢɤɭɥɹɪɧɵɯ ȿ ȼ ɩɨɥɹɯ, ɧɚɩɪɚɜɥɟɧɧɨɝɨ ɤ ɧɚɪɭɠɧɨɣ ɫɬɟɧɤɟ ɤɚɦɟɪɵ; ɛ) ɧɚɤɪɟɫɬ - ɩɨɥɭɱɢɦ ɫɬɟɥɥɚɪɚɬɨɪ ɬɢɩɚ ɜɨɫɶɦɟɪɤɢ (ɜ ɩɪɹɦɵɯ ɭɱɚɫɬɤɚɯ ɬɨɠɟ ɫɨɡɞɚɟɬɫɹ
ɦɚɝɧɢɬɧɨɟ ɩɨɥɟ). ȼ ɷɬɨɦ ɫɥɭɱɚɟ ɦɚɝɧɢɬɧɵɟ ɫɢɥɨɜɵɟ ɥɢɧɢɢ ɢɦɟɸɬ ɜɨɡɦɨɠɧɨɫɬɶ «ɩɪɨɤɪɭɱɢɜɚɬɶɫɹ» ɜɨɤɪɭɝ ɨɫɢ ɫɢɫɬɟɦɵ ɢ, ɜɨɨɛɳɟ ɝɨɜɨɪɹ, ɧɟ ɛɭɞɭɬ ɡɚɦɵɤɚɬɶɫɹ: ɦɨɠɧɨ ɩɨɤɚɡɚɬɶ, ɱɬɨ ɧɚ ɤɚɠɞɨɦ “ɨɛɯɨɞɟ” ɫɢɥɨɜɚɹ ɥɢɧɢɹ ɩɨɜɨɪɚɱɢɜɚɟɬɫɹ ɧɚ ɭɱɟɬɜɟɪɟɧɧɵɣ ɩɪɨɫɬɪɚɧɫɬɜɟɧɧɵɣ ɭɝɨɥ ɦɟɠɞɭ ɬɨɪɨɢɞɚɥɶɧɵɦɢ ɭɱɚɫɬɤɚɦɢ, ɬɟɦ ɫɚɦɵɦ ɫɬɚɧɨɜɢɬɫɹ ɜɢɧɬɨɜɨɣ ɥɢɧɢɟɣ ɢ ɪɟɚɥɢɡɭɟɬɫɹ ɷɮɮɟɤɬ ɜɪɚɳɚɬɟɥɶɧɨɝɨ ɩɪɟɨɛɪɚɡɨɜɚɧɢɹ ɫ ɤɨɦɩɟɧɫɚɰɢɟɣ ɬɨɪɨɢɞɚɥɶɧɨɝɨ ɞɪɟɣɮɚ.
ɗɬɨ ɠɟ ɦɨɠɧɨ ɨɛɴɹɫɧɢɬɶ ɧɟɫɤɨɥɶɤɨ ɩɪɨɳɟ: ɜ ɪɟɣɫɬɪɟɤɟ ɩɪɢ ɩɟɪɟɯɨɞɟ ɨɬ ɥɟɜɨɣ ɩɨɥɨɜɢɧɵ ɬɨɪɚ ɤ ɩɪɚɜɨɣ (ɪɢɫ.2.7,ɚ) ɦɟɧɹɟɬɫɹ ɧɚɩɪɚɜɥɟɧɢɟ ɭ ɜɟɤɬɨɪɨɜ ȼ ɢ ȼ, ɬɚɤ ɱɬɨ ɧɚɩɪɚɜɥɟɧɢɟ ɫɤɨɪɨɫɬɢ ɞɪɟɣɮɚ v&d B B ɫɨɯɪɚɧɹɟɬɫɹ, ɜɨɡɦɨɠɧɚ ɩɨɥɹɪɢɡɚɰɢɹ ɩɥɚɡɦɵ, ɜɨɡɧɢɤɧɨɜɟɧɢɟ ɷɥɟɤɬɪɢɱɟɫɤɨɝɨ ɩɨɥɹ ɢ ɬ.ɞ. ȼ ɫɬɟɥɥɚɪɚɬɨɪɟ ɬɢɩɚ «ɜɨɫɶɦɟɪɤɢ» ɋɩɢɬɰɟɪɚ ɩɪɢ ɩɟɪɟɯɨɞɟ ɨɬ ɥɟɜɨɣ ɩɨɥɨɜɢɧɵ ɬɨɪɚ ɤ ɩɪɚɜɨɣ (ɪɢɫ.2.7,ɛ), ɩɪɢ ɩɪɟɠɧɟɣ ɨɪɢɟɧɬɚɰɢɢ ɜɟɤɬɨɪɨɜȼ, ɡɚ ɫɱɟɬ ɷɮɮɟɤɬɚ ɜɪɚɳɚɬɟɥɶɧɨɝɨ ɩɪɟɨɛɪɚɡɨɜɚɧɢɹ ɜɨɫɫɬɚɧɚɜɥɢɜɚɟɬɫɹ ɧɚɩɪɚɜɥɟɧɢɟ ɜɟɤɬɨɪɚ ȼ, ɬɚɤ ɱɬɨ ɧɚɩɪɚɜɥɟɧɢɟ ɫɤɨɪɨɫɬɢ ɞɪɟɣɮɚ v&d ɦɟɧɹɟɬɫɹ ɧɚ ɩɪɨɬɢɜɨɩɨɥɨɠɧɨɟ.
ɉɨɥɹɪɢɡɚɰɢɹ ɧɟɜɨɡɦɨɠɧɚ − ɤɚɤ ɛɵ ɫɨɡɞɚɸɬɫɹ ɞɜɚ ɨɞɢɧɚɤɨɜɵɯ ɷɥɟɤɬɪɢɱɟɫɤɢɯ ɩɨɥɹ, ɧɚɩɪɚɜɥɟɧɧɵɯ ɚɧɬɢɩɚɪɚɥɥɟɥɶɧɨ, ɬ.ɟ. ɤɨɦɩɟɧɫɢɪɭɸɳɢɯ ɞɪɭɝ ɞɪɭɝɚ.
Ɋɚɫɱɟɬɵ ɩɨɤɚɡɚɥɢ (ɢ ɨɩɵɬ ɩɨɞɬɜɟɪɞɢɥ), ɱɬɨ ɜɦɟɫɬɨ ɩɪɨɫɬɪɚɧɫɬɜɟɧɧɨɝɨ ɩɟɪɟɤɪɟɳɢɜɚɧɢɹ ɤɨɧɰɨɜ, ɬɨ ɟɫɬɶ ɜɦɟɫɬɨ ɫɨɡɞɚɧɢɹ ɦɚɝɧɢɬɧɨɣ ɫɢɫɬɟɦɵ ɫ ɩɪɨɫɬɪɚɧɫɬɜɟɧɧɨɣ ɨɫɶɸ, ɱɬɨ ɹɜɥɹɟɬɫɹ ɞɨɫɬɚɬɨɱɧɨ ɫɥɨɠɧɨɣ ɬɟɯɧɢɱɟɫɤɢ ɡɚɞɚɱɟɣ, ɦɨɠɧɨ ɧɚ ɬɨɪɨɢɞɚɥɶɧɵɟ ɱɚɫɬɢ ɪɟɣɫɬɪɟɤɚ ɧɚɤɥɚɞɵɜɚɬɶ ɞɨɩɨɥɧɢɬɟɥɶɧɵɟ ɫɩɟɰɢɚɥɶɧɵɟ ɦɧɨɝɨɡɚɯɨɞɧɵɟ (ɨɛɵɱɧɨ ɞɜɭɯɢɥɢ ɬɪɟɯɡɚɯɨɞɧɵɟ) ɨɛɦɨɬɤɢ. ɉɪɢ ɷɬɨɦ ɬɨɤɢ ɜ ɫɨɫɟɞɧɢɯ ɜɢɬɤɚɯ ɜɵɛɢɪɚɸɬɫɹ ɬɟɤɭɳɢɦɢ ɜ ɩɪɨɬɢɜɨɩɨɥɨɠɧɵɯ ɧɚɩɪɚɜɥɟɧɢɹɯ (ɪɢɫ.2.7,ɜ). ȼ ɬɚɤɨɣ ɫɢɫɬɟɦɟ ɬɚɤɠɟ ɜɨɡɧɢɤɚɟɬ ɜɪɚɳɚɬɟɥɶɧɨɟ ɩɪɟɨɛɪɚɡɨɜɚɧɢɟ ɫɢɥɨɜɵɯ ɥɢɧɢɣ ɦɚɝɧɢɬɧɨɝɨ ɩɨɥɹ ɢ ɫɬɚɧɨɜɢɬɫɹ ɜɨɡɦɨɠɧɵɦ ɨɛɪɚɡɨɜɚɧɢɟ ɜɥɨɠɟɧɧɵɯ ɞɪɭɝ ɜ ɞɪɭɝɚ ɡɚɦɤɧɭɬɵɯ ɦɚɝɧɢɬɧɵɯ ɩɨɜɟɪɯɧɨɫɬɟɣ.
ɉɪɚɜɞɚ, ɷɬɢ ɩɨɜɟɪɯɧɨɫɬɢ ɧɚɯɨɞɹɬɫɹ ɜɧɭɬɪɢ ɧɟɤɨɬɨɪɨɣ ɝɪɚɧɢɱɧɨɣ, ɧɚɡɵɜɚɟɦɨɣ ɫɟɩɚɪɚɬɪɢɫɨɣ, ɡɚɩɨɥɧɹɸɬ ɧɟ ɜɫɟ ɫɟɱɟɧɢɟ ɤɚɦɟɪɵ ɢ ɢɦɟɸɬ ɞɨɜɨɥɶɧɨ ɫɥɨɠɧɭɸ ɮɨɪɦɭ. ɇɨ ɫɭɳɟɫɬɜɨ ɞɟɥɚ ɫɨɯɪɚɧɹɟɬɫɹ: ɥɸɛɨɣ ɫɬɟɥɥɚɪɚɬɨɪ ɹɜɥɹɟɬɫɹ ɢɞɟɚɥɶɧɨɣ ɦɚɝɧɢɬɧɨɣ ɥɨɜɭɲɤɨɣ ɞɥɹ ɨɬɞɟɥɶɧɵɯ ɱɚɫɬɢɰ ɢ ɫɩɨɫɨɛɟɧ ɯɨɪɨɲɨ ɭɞɟɪɠɢɜɚɬɶ ɩɥɚɡɦɭ ɛɟɡ ɩɪɨɩɭɫɤɚɧɢɹ ɞɨɩɨɥɧɢɬɟɥɶɧɨɝɨ ɬɨɤɚ ɜ ɧɟɣ. Ɍɚɤ ɤɚɤ ɜ ɬɚɤɢɯ ɫɢɫɬɟɦɚɯ ɢɦɟɸɬɫɹ ɦɚɝɧɢɬɧɵɟ ɫɢɥɨɜɵɟ ɥɢɧɢɢ, ɧɟ ɜɵɯɨɞɹɳɢɟ ɡɚ ɩɪɟɞɟɥɵ ɫɢɫɬɟɦɵ (ɡɚɦɤɧɭɬɵɟ ɢɥɢ ɭɯɨɞɹɳɢɟ ɜ ɛɟɫɤɨɧɟɱɧɨɫɬɶ ɧɚ ɡɚɦɤɧɭɬɨɣ ɩɨɜɟɪɯɧɨɫɬɢ), ɬɨ ɩɨɞɨɛɧɵɟ ɫɢɫɬɟɦɵ ɧɚɡɵɜɚɸɬ ɡɚɤɪɵɬɵɦɢ (ɢɧɨɝɞɚ ɡɚɦɤɧɭɬɵɦɢ).
§ 18. Ⱥɞɢɚɛɚɬɢɱɟɫɤɢɟ ɢɧɜɚɪɢɚɧɬɵ
Ʉɚɤ ɢɡɜɟɫɬɧɨ ɢɡ ɦɟɯɚɧɢɤɢ, ɥɸɛɚɹ ɦɟɯɚɧɢɱɟɫɤɚɹ ɫɢɫɬɟɦɚ, ɫɨɜɟɪɲɚɸɳɚɹ ɮɢɧɢɬɧɨɟ ɞɜɢɠɟɧɢɟ, ɧɚɩɪɢɦɟɪ, ɦɚɬɟɦɚɬɢɱɟɫɤɢɣ ɦɚɹɬɧɢɤ ɢɥɢ ɝɪɭɡ, ɩɨɞɜɟɲɟɧɧɵɣ ɧɚ ɩɪɭɠɢɧɤɟ,
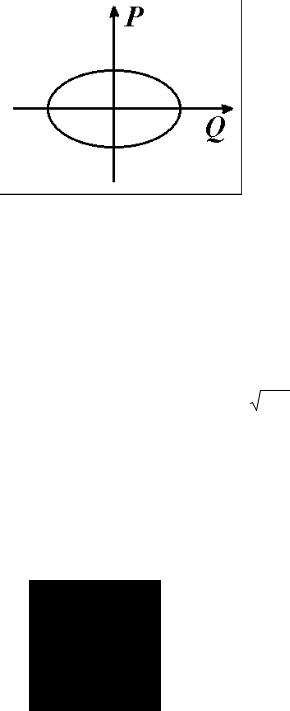
ɢɦɟɟɬ ɬɪɚɟɤɬɨɪɢɸ, ɡɚɧɢɦɚɸɳɭɸ ɜ ɮɚɡɨɜɨɦ |
ɩɪɨɫɬɪɚɧɫɬɜɟ ɨɝɪɚɧɢɱɟɧɧɭɸ ɨɛɥɚɫɬɶ (ɜ |
|||||||
|
ɩɪɨɫɬɟɣɲɟɦ ɫɥɭɱɚɟ ɨɞɧɨɦɟɪɧɨɝɨ ɞɜɢɠɟɧɢɹ ɷɬɨ |
|||||||
|
ɩɥɨɫɤɨɫɬɶ ɨɛɨɛɳɟɧɧɨɝɨ ɢɦɩɭɥɶɫɚ ɢ ɨɛɨɛɳɟɧɧɨɣ |
|||||||
|
ɤɨɨɪɞɢɧɚɬɵ, ɪɢɫ.2.8). ȿɫɥɢ ɷɧɟɪɝɢɹ ɷɬɨɣ ɫɢɫɬɟɦɵ |
|||||||
|
ɫɨɯɪɚɧɹɟɬɫɹ, ɬɨ ɬɪɚɟɤɬɨɪɢɹ, ɨɬɜɟɱɚɸɳɚɹ ɡɚɞɚɧɧɨɣ |
|||||||
|
ɷɧɟɪɝɢɢ W, ɹɜɥɹɟɬɫɹ ɡɚɦɤɧɭɬɨɣ. Ɉɯɜɚɬɵɜɚɟɦɚɹ ɷɬɨɣ |
|||||||
|
ɬɪɚɟɤɬɨɪɢɟɣ ɩɥɨɳɚɞɶ, ɨɱɟɜɢɞɧɨ, ɹɜɥɹɟɬɫɹ ɬɨɱɧɵɦ |
|||||||
|
ɢɧɬɟɝɪɚɥɨɦ |
ɞɜɢɠɟɧɢɹ. |
ɋɭɳɟɫɬɜɟɧɧɨ, |
ɱɬɨ |
||||
|
ɩɪɢɛɥɢɠɟɧɧɨɟ ɫɨɯɪɚɧɟɧɢɟ ɷɬɨɣ ɩɥɨɳɚɞɢ ɢɦɟɟɬ |
|||||||
|
ɦɟɫɬɨ ɢ ɬɨɦ ɫɥɭɱɚɟ, ɤɨɝɞɚ ɷɧɟɪɝɢɹ ɫɢɫɬɟɦɵ ɦɟɧɹɟɬɫɹ |
|||||||
|
ɫɨ ɜɪɟɦɟɧɟɦ ɩɨɞ ɞɟɣɫɬɜɢɟɦ ɤɚɤɨɝɨ-ɥɢɛɨ ɜɨɡɦɭɳɟɧɢɹ |
|||||||
|
(ɧɚɩɪɢɦɟɪ, ɫɥɚɛɨɝɨ ɬɪɟɧɢɹ, ɢɥɢ ɢɡɦɟɧɟɧɢɹ ɞɥɢɧɵ |
|||||||
Ɋɢɫ.2.8. «Ɏɚɡɨɜɵɣ ɩɨɪɬɪɟɬ» |
ɦɚɹɬɧɢɤɚ |
ɢ |
ɬɨɦɭ |
ɩɨɞɨɛɧɨɟ), ɧɨ ɷɬɨ ɢɡɦɟɧɟɧɢɟ |
||||
ɨɞɧɨɦɟɪɧɨɝɨ ɨɫɰɢɥɥɹɬɨɪɚ |
ɦɟɞɥɟɧɧɨɟ |
|
ɩɨ |
ɫɪɚɜɧɟɧɢɸ |
ɫ |
ɩɟɪɢɨɞɨɦ |
||
|
ɧɟɜɨɡɦɭɳɟɧɧɨɝɨ ɞɜɢɠɟɧɢɹ. Ɍɟɩɟɪɶ ɷɬɚ ɩɥɨɳɚɞɶ ɭɠɟ |
|||||||
ɧɟ ɹɜɥɹɟɬɫɹ ɬɨɱɧɵɦ ɢɧɬɟɝɪɚɥɨɦ ɞɜɢɠɟɧɢɹ, ɢ ɫɨɯɪɚɧɟɧɢɟ ɢɦɟɟɬ ɦɟɫɬɨ ɥɢɲɶ ɜ ɫɪɟɞɧɟɦ ɩɨ ɩɟɪɢɨɞɭ ɧɟɜɨɡɦɭɳɟɧɧɨɝɨ ɞɜɢɠɟɧɢɹ. ȼ ɷɬɨɦ ɫɥɭɱɚɟ ɝɨɜɨɪɹɬ ɨ ɫɨɯɪɚɧɟɧɢɢ ɚɞɢɚɛɚɬɢɱɟɫɤɨɝɨ ɢɧɜɚɪɢɚɧɬɚ. ɉɨ ɪɚɡɦɟɪɧɨɫɬɢ ɷɬɚ ɩɥɨɳɚɞɶ ɩɪɨɩɨɪɰɢɨɧɚɥɶɧɚ ɩɪɨɢɡɜɟɞɟɧɢɸ ɫɪɟɞɧɟɣ ɡɚ ɩɟɪɢɨɞ ɷɧɟɪɝɢɢ ɱɚɫɬɢɰɵ ɧɚ ɜɟɥɢɱɢɧɭ ɷɬɨɝɨ ɩɟɪɢɨɞɚ:
J ~ < W > T . |
(2.44) |
ɉɨɷɬɨɦɭ, ɟɫɥɢ ɩɪɢ ɢɡɦɟɧɟɧɢɢ ɤɚɤɨɝɨ-ɥɢɛɨ ɩɚɪɚɦɟɬɪɚ ɫɢɫɬɟɦɵ ɩɟɪɢɨɞ ɞɜɢɠɟɧɢɹ ɭɦɟɧɶɲɚɟɬɫɹ (ɧɚɩɪɢɦɟɪ, ɞɥɹ ɦɚɬɟɦɚɬɢɱɟɫɤɨɝɨ ɦɚɹɬɧɢɤɚ ɩɟɪɢɨɞ, ɤɚɤ ɢɡɜɟɫɬɧɨ, ɨɩɪɟɞɟɥɹɟɬɫɹ ɫɨɨɬɧɨɲɟɧɢɟɦ T = 2π l / g , ɢ ɩɟɪɢɨɞ ɭɦɟɧɶɲɚɟɬɫɹ ɫ ɭɦɟɧɶɲɟɧɢɟɦ ɞɥɢɧɵ
ɦɚɹɬɧɢɤɚ), ɬɨ ɟɺ ɷɧɟɪɝɢɹ ɜ ɫɪɟɞɧɟɦ ɜɨɡɪɚɫɬɚɟɬ.
ɉɪɢɧɰɢɩ ɚɞɢɚɛɚɬɢɱɟɫɤɨɣ ɢɧɜɚɪɢɚɧɬɧɨɫɬɢ ɧɚɯɨɞɢɬ ɜɚɠɧɵɟ ɩɪɢɥɨɠɟɧɢɹ ɤ ɩɪɨɛɥɟɦɟ ɭɞɟɪɠɚɧɢɹ ɩɥɚɡɦɵ − ɩɨ ɧɟɨɛɯɨɞɢɦɨɫɬɢ ɬɪɚɟɤɬɨɪɢɢ ɱɚɫɬɢɰ ɞɨɥɠɧɵ ɛɵɬɶ ɮɢɧɢɬɧɵɦɢ. Ɋɚɫɫɦɨɬɪɢɦ ɤɪɚɬɤɨ ɧɟɤɨɬɨɪɵɟ ɩɪɢɥɨɠɟɧɢɹ ɷɬɨɝɨ ɩɪɢɧɰɢɩɚ ɞɥɹ ɫɥɭɱɚɹ ɞɜɢɠɟɧɢɹ ɱɚɫɬɢɰ ɜ ɦɚɝɧɢɬɧɨɦ ɩɨɥɟ.
ɂɧɜɚɪɢɚɧɬɧɨɫɬɶ ɦɚɝɧɢɬɧɨɝɨ ɦɨɦɟɧɬɚ µ ɱɚɫɬɢɰɵ ɜɨ ɜɪɟɦɟɧɢ
ȿɫɥɢ ɡɚɪɹɠɟɧɧɚɹ ɱɚɫɬɢɰɚ ɞɜɢɠɟɬɫɹ ɜ ɨɞɧɨɪɨɞɧɨɦ, ɧɨ ɦɟɧɹɸɳɟɦɫɹ ɜɨ ɜɪɟɦɟɧɢ ɦɚɝɧɢɬɧɨɦ ɩɨɥɟ, ɬɨ ɟɟ ɥɚɪɦɨɪɨɜɫɤɢɣ ɪɚɞɢɭɫ ɢ ɩɟɪɩɟɧɞɢɤɭɥɹɪɧɚɹ ɫɤɨɪɨɫɬɶ ɛɭɞɭɬ ɦɟɧɹɬɶɫɹ. ɗɬɨ ɩɪɨɢɫɯɨɞɢɬ ɩɨɬɨɦɭ, ɱɬɨ ɢɧɞɭɰɢɪɨɜɚɧɧɨɟ ɦɟɧɹɸɳɢɦɫɹ ɦɚɝɧɢɬɧɵɦ ɩɨɥɟɦ ɷɥɟɤɬɪɢɱɟɫɤɨɟ ɛɭɞɟɬ ɭɫɤɨɪɹɬɶ
(ɢɥɢ ɡɚɦɟɞɥɹɬɶ) ɱɚɫɬɢɰɭ.
ȼɵɛɟɪɟɦ ɰɢɥɢɧɞɪɢɱɟɫɤɭɸ ɫɢɫɬɟɦɭ ɤɨɨɪɞɢɧɚɬ ɬɚɤ, ɱɬɨɛɵ ɜɟɤɬɨɪ ɧɚɩɪɹɠɟɧɧɨɫɬɢ&ɦɚɝɧɢɬɧɨɝɨ ɩɨɥɹ ɛɵɥ ɩɚɪɚɥɥɟɥɟɧ ɨɫɢ z ɷɬɨɣ ɫɢɫɬɟɦɵ (ɫɦ. ɪɢɫ.2.9), ɬɨɝɞɚ B( t ) = B( t )e&z , ɝɞɟ e&z - ɫɨɨɬɜɟɬɫɬɜɭɸɳɢɣ ɟɞɢɧɢɱɧɵɣ ɜɟɤɬɨɪ. ɂɡ ɡɚɤɨɧɚ ɢɧɞɭɤɰɢɢ
Ɋɢɫ.2.9. Ƚɟɨɦɟɬɪɢɹ ɩɨɥɟɣ |
|
1 |
|
∂ |
|
& 1 ∂ |
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||
− c |
|
∂ t Bz |
= rotz E ≡ ρ ∂ρ ρEϕ , |
(2.45) |
|||||||||||
(ɦɚɝɧɢɬɧɨɟ ɩɨɥɟ - ɭɛɵɜɚɟɬ) |
|
||||||||||||||
|
1 |
|
ρ |
|
ɧɚɯɨɞɢɦ |
|
|
|
|
|
|
|
|
|
|
E = − |
|
B( t ) . |
|
|
|
|
|
|
|
|
|
|
(2.46) |
||
|
|
|
|
|
|
|
|
|
|
|
|
||||
ϕ |
2 |
|
c |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
ɉɨɞɫɬɚɜɥɹɹ ɬɟɩɟɪɶ ɷɬɢ ɩɨɥɹ ɜ ɨɫɬɚɜɲɢɟɫɹ ɭɪɚɜɧɟɧɢɹ Ɇɚɤɫɜɟɥɥɚ, ɨɛɧɚɪɭɠɢɜɚɟɦ, ɱɬɨ
1 |
|
∂ |
E |
|
= rot |
|
B |
|
≡ 0, |
||
|
|
|
z |
||||||||
c ∂ t |
ϕ |
ϕ |
|
|
|||||||
div B& ≡ 0, |
|
|
|
(2.47) |
|||||||
div E& = |
1 |
|
∂ |
E |
|
≡ 0. |
|||||
|
|
|
|||||||||
|
|
|
|
|
ρ ∂ ϕ |
|
ϕ |
|
|||
|
|
|
|
|
|
|
|
|
|||
ɉɨɷɬɨɦɭ ɭɪɚɜɧɟɧɢɹ Ɇɚɤɫɜɟɥɥɚ ɭɞɨɜɥɟɬɜɨɪɹɸɬɫɹ ɬɨɠɞɟɫɬɜɟɧɧɨ ɩɪɢ ɜɵɛɨɪɟ ɥɢɧɟɣɧɨɣ ɡɚɜɢɫɢɦɨɫɬɢ ɧɚɩɪɹɠɟɧɧɨɫɬɢ ɦɚɝɧɢɬɧɨɝɨ ɩɨɥɹ ɨɬ ɜɪɟɦɟɧɢ, ɬɚɤ ɱɬɨ:
B( t ) = B |
+ B |
t , |
E |
= − |
1 |
ρ |
B |
(2.48) |
|
2 |
c |
||||||||
0 |
0 |
|
ϕ |
|
0 |
|
ɝɞɟ B0 - ɩɨɫɬɨɹɧɧɚɹ ɜɟɥɢɱɢɧɚ (ɫɤɨɪɨɫɬɶ ɢɡɦɟɧɟɧɢɹ ɩɨɥɹ), ɤɨɬɨɪɚɹ ɦɨɠɟɬ ɛɵɬɶ ɤɚɤ ɩɨɥɨɠɢɬɟɥɶɧɨɣ (ɩɨɥɟ ɪɚɫɬɟɬ), ɬɚɤ ɢ ɨɬɪɢɰɚɬɟɥɶɧɨɣ (ɩɨɥɟ ɭɛɵɜɚɟɬ); B0 - ɧɚɱɚɥɶɧɨɟ ɡɧɚɱɟɧɢɟ ɩɨɥɹ.
ɉɨɥɭɱɟɧɧɨɟ ɪɟɲɟɧɢɟ ɭɪɚɜɧɟɧɢɣ Ɇɚɤɫɜɟɥɥɚ − ɬɨɱɧɨɟ, ɧɨ ɧɟɫɤɨɥɶɤɨ ɢɫɤɭɫɫɬɜɟɧɧɨɟ: ɬɪɭɞɧɨ ɩɪɟɞɫɬɚɜɢɬɶ ɫɟɛɟ ɫɢɬɭɚɰɢɸ, ɤɨɝɞɚ ɦɚɝɧɢɬɧɨɟ ɩɨɥɟ ɧɚɪɚɫɬɚɟɬ ɫɪɚɡɭ ɜɨ ɜɫɟɦ ɩɪɨɫɬɪɚɧɫɬɜɟ. ɇɚ ɩɪɚɤɬɢɤɟ ɱɚɫɬɨ ɢɫɩɨɥɶɡɭɸɬ ɩɪɢɛɥɢɠɟɧɧɨɟ ɪɟɲɟɧɢɟ, ɫɱɢɬɚɹ, ɱɬɨ ɩɨɪɨɠɞɚɸɳɢɟ ɦɚɝɧɢɬɧɨɟ ɩɨɥɟ ɬɨɤɢ ɦɟɧɹɸɬɫɹ ɧɚɫɬɨɥɶɤɨ ɦɟɞɥɟɧɧɨ, ɱɬɨ ɬɨɤɚɦɢ ɫɦɟɳɟɧɢɹ (ɢ, ɬɟɦ ɫɚɦɵɦ, ɜɨɥɧɨɜɵɦ ɩɪɨɰɟɫɫɨɦ ɭɫɬɚɧɨɜɥɟɧɢɹ ɩɨɥɹ) ɦɨɠɧɨ ɩɪɟɧɟɛɪɟɱɶ. Ɍɨɝɞɚ ɮɨɪɦɭɥɵ
B&( t ) = B( t )e& |
, |
E& = − |
1 |
|
ρ |
B( t )e& |
(2.49) |
|
|
||||||
z |
|
2 |
|
c |
ϕ |
|
|
|
|
|
|
|
|||
ɩɪɢɛɥɢɠɟɧɧɨ ɨɩɢɫɵɜɚɸɬ ɪɚɫɩɪɟɞɟɥɟɧɢɟ ɩɨɥɟɣ ɩɪɢ ɩɪɨɢɡɜɨɥɶɧɨɣ ɡɚɜɢɫɢɦɨɫɬɢ ȼ(t), ɦɟɞɥɟɧɧɨɣ ɧɚ ɦɚɫɲɬɚɛɚɯ ɜɪɟɦɟɧɢ ∆t~L/c, ɝɞɟ L - ɪɚɡɦɟɪ ɨɛɥɚɫɬɢ, ɡɚɧɢɦɚɟɦɨɣ ɩɨɥɟɦ.
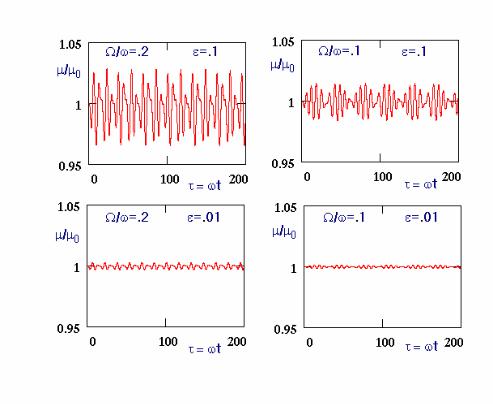
Ɋɢɫ.2.10. ɂɥɥɸɫɬɪɚɰɢɹ ɫɨɯɪɚɧɟɧɢɹ ɩɨɩɟɪɟɱɧɨɝɨ ɚɞɢɚɛɚɬɢɱɟɫɤɨɝɨ ɢɧɜɚɪɢɚɧɬɚ ɜ ɫɥɚɛɨ ɩɟɪɟɦɟɧɧɨɦ, ɦɟɞɥɟɧɧɨ ɨɫɰɢɥɥɢɪɭɸɳɟɦ ɩɨɥɟ ȼ=ȼ0(1+εcosΩt); ω - ɥɚɪɦɨɪɨɜɫɤɚɹ ɱɚɫɬɨɬɚ, µ0 - ɧɚɱɚɥɶɧɨɟ ɡɧɚɱɟɧɢɟ
Ⱦɥɹ ɢɥɥɸɫɬɪɚɰɢɢ ɫɨɯɪɚɧɟɧɢɹ µ − ɦɚɝɧɢɬɧɨɝɨ ɦɨɦɟɧɬɚ ɢɥɢ ɩɨɩɟɪɟɱɧɨɝɨ ɚɞɢɚɛɚɬɢɱɟɫɤɨɝɨ ɢɧɜɚɪɢɚɧɬɚ − ɩɪɢ ɞɜɢɠɟɧɢɢ ɱɚɫɬɢɰɵ ɜ ɩɟɪɟɦɟɧɧɨɦ ɦɚɝɧɢɬɧɨɦ ɩɨɥɟ ɨɝɪɚɧɢɱɢɦɫɹ ɝɪɭɛɵɦ ɩɪɢɛɥɢɠɟɧɢɟɦ, ɫɱɢɬɚɹ, ɱɬɨ ɪɚɞɢɚɥɶɧɚɹ ɫɤɨɪɨɫɬɶ ɬɨɠɞɟɫɬɜɟɧɧɨ ɪɚɜɧɚ ɧɭɥɸ ɢ ɪɚɞɢɭɫ ɨɪɛɢɬɵ − ɩɨɫɬɨɹɧɧɵɣ. ȼ ɷɬɨɦ ɩɪɢɛɥɢɠɟɧɢɢ ɭɪɚɜɧɟɧɢɹ ɞɜɢɠɟɧɢɹ ɫɜɨɞɹɬɫɹ ɤ ɜɢɞɭ

mv |
|
= eE , |
mv |
|
= − |
e |
ρB |
ϕ |
ϕ |
|
|||||
|
ϕ |
|
|
c |
|
||
|
|
|
|
|
|
|
ɢ, ɤɚɤ ɧɟ ɬɪɭɞɧɨ ɩɪɨɜɟɪɢɬɶ, ɞɚɸɬ ɫɨɨɬɧɨɲɟɧɢɟ
d §vϕ2 |
· |
= |
vϕ2 dB |
. |
||||
¨ |
|
¸ |
|
|
|
|||
|
¨ |
|
¸ |
|
|
|
|
|
dt © |
2 |
¹ |
|
2B dt |
|
|||
ɗɬɨ ɨɡɧɚɱɚɟɬ, ɱɬɨ ɨɬɧɨɲɟɧɢɟ
v2
Bϕ = const
ɫɨɯɪɚɧɹɟɬɫɹ. ɉɟɪɟɨɛɨɡɧɚɱɢɜ vϕ→v , ɩɨɥɭɱɢɦ ɨɤɨɧɱɚɬɟɥɶɧɨ
mv2 = µ = const . 2B
(2.50)
(2.51)
(2.52)
(2.53)
Ƚɪɭɛɨɟ ɩɪɢɛɥɢɠɟɧɢɟ, ɢɫɩɨɥɶɡɨɜɚɧɧɨɟ ɜɵɲɟ, ɜɨɜɫɟ ɧɟ ɨɛɹɡɚɬɟɥɶɧɨ. Ⱦɟɬɚɥɶɧɵɟ ɪɚɫɱɟɬɵ (ɫɦ., ɧɚɩɪɢɦɟɪ [11]) ɩɨɤɚɡɵɜɚɸɬ ɫɨɯɪɚɧɟɧɢɟ µ ɜ ɨɛɳɟɦ ɫɥɭɱɚɟ ɜ ɭɫɥɨɜɢɹɯ ɩɪɢɦɟɧɢɦɨɫɬɢ ɚɞɢɚɛɚɬɢɱɟɫɤɨɝɨ ɩɪɢɛɥɢɠɟɧɢɹ. Ⱦɥɹ ɢɥɥɸɫɬɪɚɰɢɢ «ɤɚɱɟɫɬɜɚ» ɫɨɯɪɚɧɟɧɢɹ µ ɧɚ ɪɢɫ.2.10 ɩɪɢɜɟɞɟɧɵ ɪɟɡɭɥɶɬɚɬɵ ɬɨɱɧɵɯ ɱɢɫɥɟɧɧɵɯ ɪɚɫɱɟɬɨɜ ɷɬɨɝɨ ɩɚɪɚɦɟɬɪɚ ɞɥɹ ɱɚɫɬɧɨɝɨ ɜɢɞɚ ɨɫɰɢɥɥɢɪɭɸɳɟɝɨ ɩɨɥɹ.
ɂɧɜɚɪɢɚɧɬɧɨɫɬɶ µ ɱɚɫɬɢɰɵ ɜ ɩɨɫɬɨɹɧɧɨɦ ɜɨ ɜɪɟɦɟɧɢ ɢ ɧɟɨɞɧɨɪɨɞɧɨɦ ɜ
ɩɪɨɫɬɪɚɧɫɬɜɟ ɦɚɝɧɢɬɧɨɦ ɩɨɥɟ
Ʉɨɝɞɚ ɩɨɥɟ ȼ ɩɨɫɬɨɹɧɧɨɟ ɜɨ ɜɪɟɦɟɧɢ, ɧɨ ɦɟɞɥɟɧɧɨ ɦɟɧɹɟɬɫɹ ɜ ɩɪɨɫɬɪɚɧɫɬɜɟ, ɬɨ ɩɪɢ ɩɟɪɟɯɨɞɟ ɱɚɫɬɢɰɵ ɢɡ ɫɥɚɛɨɝɨ ɩɨɥɹ ɜ ɛɨɥɟɟ ɫɢɥɶɧɨɟ ɧɚ ɧɟɟ ɞɟɣɫɬɜɭɟɬ ɫɢɥɚ (ɪɢɫ.2.11):
|
F = −µ |
|
∂ B |
|
= m |
dv|| |
; |
(2.54) |
||||||
|
|
|
|
|
|
|
||||||||
|
z |
|
|
|
|
∂ z |
|
|
|
dt |
|
|
||
|
|
|
|
|
|
|
|
|
|
|
||||
|
Ɂɞɟɫɶ |
|
dz |
|
|
|
|
|
|
|
|
|
|
|
|
v |
= |
. |
|
|
|
|
|
|
|
(2.55) |
|||
|
|
|
|
|
|
|
|
|
||||||
|
|| |
|
dt |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Ɋɢɫ.2.11. ȼɵɬɚɥɤɢɜɚɧɢɟ ɡɚɪɹɠɟɧɧɨɣ |
ɉɨɫɥɟ ɩɪɟɨɛɪɚɡɨɜɚɧɢɹ ɜɞɨɥɶ ɬɪɚɟɤɬɨɪɢɢ ɩɨɥɭɱɢɦ |
|||||||||||||
ɱɚɫɬɢɰɵ ɧɟɨɞɧɨɪɨɞɧɵɦ ɦɚɝɧɢɬɧɵɦ |
− |
µ |
dB |
= |
d §mv||2 |
· |
|
(2.56) |
||||||
ɩɨɥɟɦ. |
|
|
|
¨ |
|
|
¸ . |
|||||||
|
|
|
|
|
|
|
|
|
¨ |
|
|
¸ |
|
|
|
|
|
dt |
|
|
dt © |
2 |
¹ |
|
|
||||
Ɍɚɤ ɤɚɤ ɩɨɥɧɚɹ ɷɧɟɪɝɢɹ ɩɪɢ ɞɜɢɠɟɧɢɢ ɜ ɦɚɝɧɢɬɧɨɦ ɩɨɥɟ ɫɨɯɪɚɧɹɟɬɫɹ
|
mv||2 |
|
|
|
mv2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
+ |
|
|
|
= const |
, |
|
|
|
|||
2 |
|
|
2 |
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
ɬɨ ɩɨɥɭɱɚɟɦ |
|
|
|
|
|
|
|
|
|
|
|||||
|
|
dB |
|
|
§ |
2 |
· |
|
d |
|
|||||
− µ |
|
= − |
d |
¨ |
mv |
|
¸ |
− |
( µB ) ; |
||||||
|
|
2 |
|
dt |
|||||||||||
|
|
|
dt |
|
dt © |
¹ |
|
|
|||||||
ɱɬɨ ɜɨɡɦɨɠɧɨ, ɬɨɥɶɤɨ ɟɫɥɢ
µ=const.
(2.57)
(2.58)
ɇɟɬɨɱɧɨɫɬɶ, ɞɨɩɭɳɟɧɧɚɹ ɩɪɢ ɜɵɜɨɞɟ, ɜ ɞɚɧɧɨɦ ɫɥɭɱɚɟ ɫɜɹɡɚɧɚ ɫ ɬɟɦ, ɱɬɨ ɢɡɦɟɧɟɧɢɹ ȼ ɜ
ɩɟɪɩɟɧɞɢɤɭɥɹɪɧɨɦ ɧɚɩɪɚɜɥɟɧɢɢ ɧɟ ɭɱɬɟɧɵ. ɗɬɨ ɞɨɩɭɫɬɢɦɨ ɥɢɲɶ ɩɪɢ ɦɟɞɥɟɧɧɨɦ ɢɡɦɟɧɟɧɢɢ. ȼ, ɬ.ɟ. ɟɫɥɢ ɜɵɩɨɥɧɹɟɬɫɹ ɭɫɥɨɜɢɟ (2.10). Ɉɛɨɛɳɚɹ ɭɪɚɜɧɟɧɢɹ (2.53) ɢ (2.58), ɦɨɠɧɨ ɫɤɚɡɚɬɶ, ɱɬɨ ɦɚɝɧɢɬɧɵɣ ɦɨɦɟɧɬ
ɩɪɟɞɫɬɚɜɥɹɟɬ ɫɨɛɨɣ ɚɞɢɚɛɚɬɢɱɟɫɤɢɣ ɢɧɜɚɪɢɚɧɬ ɞɜɢɠɟɧɢɹ ɡɚɪɹɠɟɧɧɨɣ ɱɚɫɬɢɰɵ ɜ ɦɟɞɥɟɧɧɨ ɢɡɦɟɧɹɸɳɟɦɫɹ ɦɚɝɧɢɬɧɨɦ ɩɨɥɟ.
Ɉɬɫɸɞɚ ɦɨɠɧɨ ɫɞɟɥɚɬɶ ɧɟɫɤɨɥɶɤɨ ɢɧɬɟɪɟɫɧɵɯ ɜɵɜɨɞɨɜ. ɂɡ ɜɩɨɥɧɟ ɨɱɟɜɢɞɧɵɯ ɚɥɝɟɛɪɚɢɱɟɫɤɢɯ
ɜɵɤɥɚɞɨɤ |
|
|
|
|
|
|
|
|
mv2 |
= |
m2 v2 c2 |
|
e2 |
B = const ρ 2 B = const Φ = const |
(2.59) |
|
2B |
e2 B2 |
|
2mc2 |
|||
|
|
|
|
|
|||
