3.2 Теплопроводность через плоскую многослойную стенку

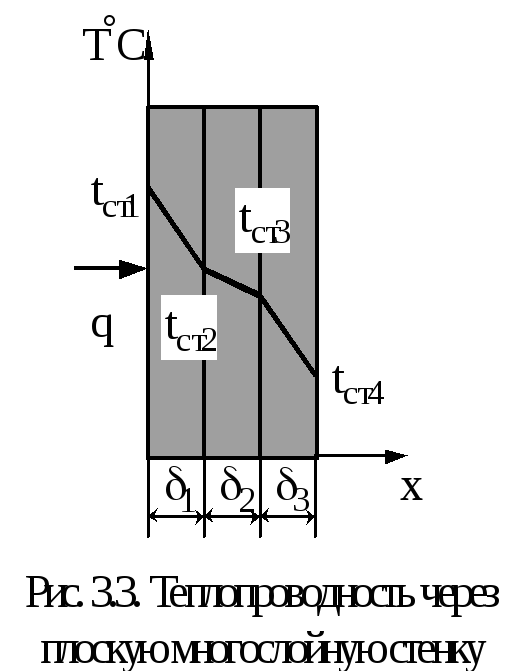
Для многослойной стенки плотность теплового потока одинакова для всех слоёв

. (3.6)

где i – порядковый номер стенки;

n – количество слоёв.

Эквивалентный коэффициент теплопроводности многослойной стенки определяется из выражения:

. (3.7)

Температура на границе раздела слоёв определяется из следующего выражения:

, (3.8)

где берётся из справочника.

Так как тепловая изоляция многослойная, первичный слой – огнеупорный, второй и третий – теплопроводный, следовательно потери теплоты в окружающую среду определяются из уравнения (3.6)

Пример: Один слой 250 мм, , . Определить температуру в центре стенки, если коэффициент теплопроводности равен .

Решение: ; .

3.3 Теплопередача через плоскую однослойную стенку при граничных условиях III-рода

Теплопередача – процесс теплообмена между двумя средами (теплоносителями), разделёнными стенкой (перегородкой). В этом случае при граничных условиях III-рода задаются температуры сред теплоносителей, коэффициенты теплоотдачи между горячей средой и стенкой и между стенкой и холодной средой, т.е. задаётся закон теплообмена. Также задаётся коэффициент теплопроводности и толщина стенки δ.

Требуется найти плотность теплового потока, тепловой поток и температуру поверхности стенки.

Согласно закону Ньютона-Рихмана плотность теплового потока между горячей средой и поверхностью стенки:

. (3.9)

По закону Фурье этот же поток передаётся теплопроводностью:

. (3.9)

Этот же тепловой поток согласно закону Ньютона-Рихмана от наружной поверхности стенки отдаётся холодной среде:

. (3.9)

Выражая из этих уравнений разности температур и складывая между собой, мы окончательно получаем выражение для плотности теплового потока q:

, . (3.10)

Обозначим величину

, (3.11)

К – коэффициент теплопередачи через плоскую однослойную однородную стенку. Он представляет собой количество теплоты, передаваемое в единицу времени через единицу поверхности при разности температур между средами в один градус. Значения коэффициентов теплопередачи для различных видов теплообмена будут даны в таблице в разделе конвективного теплообмена. Коэффициент теплопередачи всегда меньше меньшего α. Для того чтобы увеличить теплопередачу, нужно увеличить меньшее α.

. (3.12)

Тепловой поток

. (3.13)

Величина обратная коэффициенту теплопередачи – полное термическое сопротивление теплопередачи:

, (3.14)

где – термическое сопротивление теплоотдачи со стороны горячей жидкости;

– термическое сопротивление стенки (чем меньше , тем выше );

– термическое сопротивление теплоотдачи от стенки к холодной среде. .

Полное количество теплоты, передаваемое через стенку за время τ

, Дж.

Коэффициента теплопередачи не является термофизическим коэффициентом, его нет в справочниках. Он рассчитывается по формуле (3.11).

Из (3.9) легко найти температуры горячей и холодной стенок:

, (3.15)

.

3.4 Теплопередача через многослойную плоскую стенку при граничных условиях III-рода

Пусть заданы температуры сред и , коэффициенты теплоотдачи и (закон теплообмена), коэффициенты теплопроводности , и , толщина слоёв стенки , и .

Аналогично формуле (3.9) записывают уравнение сохранения плотности теплового потока q, выражая разность температур и складывая почленно полученные выражения плотности теплового потока

, , (3.16)

, . (3.17)

Коэффициент теплопередачи:

(3.18)

(3.19)

Из уравнения (3.16), определяя плотность теплового потока, находим температуры на поверхностях стенки , и температуры на границах слоёв , .