Дифференциальное уравнение теплопроводности есть аналитическое решение температурного поля (формула (1.1)). Для его вывода предполагаем, что температурное поле трёхмерное и нестационарное. Для упрощения считаем, что теплофизические коэффициенты в пределах dV и dτ постоянны. Рассмотрим элементарный объём с гранями dx, dy и dz. В декартовой системе пронизывается тепловым потоком в трёх направлениях x, y и z. Причём . Из гипотезы Фурье количество теплоты, воспринимаемое гранью вдоль оси Х

. (2.1)

Количество теплоты, выходящее в направлении оси Х

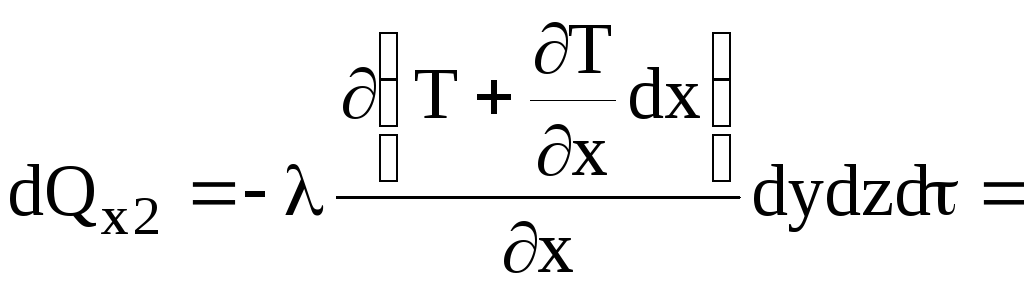(2.2)

.

Разница подведённого и отведённого количества теплот за dτ в направлении ОХ представляет собой количество теплоты, воспринятое dV вдоль ОХ путём теплопроводности

. (2.3)

По аналогии, вдоль осей ОY и OZ:

,

.

Тогда полное количество теплоты, подведённое теплопроводностью к dV:

. (2.4)

В скобках – оператор Лапласа второго порядка .

Теплота, помимо теплопроводности в dV может быть подведена от внутренних источников (электрический ток, ядерная или химическая реакция). Мощность этих источников обозначаем как . Тогда общее количество теплоты, полученное dV, будет:

.

С другой стороны это количество теплоты идёт на увеличение теплосодержания (энтальпии) dV для изобарного процесса (для изохорного – на изменение внутренней энергии)

.

Приравняем:

,

.

Коэффициент температуропроводности: – характеризует скорость изменения температуры в теле или термоинерционные свойства тела.

Окончательно дифференциальное уравнение теплопроводности с учётом внутренних источников теплоты:

, (2.5)

без учёта :

. (2.6)

Стационарный режим:

. – уравнение Лапласа (2.7)

Уравнения (2.5) – (2.6) – дифференциальные уравнения второго порядка, которые описывают бесчисленное множество процессов. Для аналитического решения конкретной задачи необходимо к ним добавить условия однозначности.

2.2 Условия однозначности

Эти условия включают в себя: геометрические, физические, начальные и граничные. Геометрические определяют форму и размеры тела. Физические условия характеризуют физические свойства тела. Начальные условия – распределение температуры в теле в начальный момент времени . Граничные характеризуют условия теплообмена на границе раздела тела и среды. Граничные условия бывают I-рода – задана температура поверхности для любого момента времени. Для простейшего случая . Граничные условия II-рода – задан закон распределения плотности теплового потока на поверхности материала. При граничных условиях II-рода происходит нагревание и охлаждение в промышленных печах. III-рода – задан закон теплообмена между поверхностью тела и средой.

Основной закон теплообмена – закон Ньютона-Рихмана, согласно которому плотность теплового потока между телом и средой прямо пропорциональна разности температур между ними:

, (2.8)

где α – коэффициент теплоотдачи . Количество теплоты, отдаваемое в единицу времени единицей площади поверхности при разности температур между поверхностью и окружающей средой в 1К.

Согласно 1-му закону термодинамики всё тепло, подведённое к поверхности тела теплопроводностью равно количеству теплоты, отданное этой поверхностью теплоотдачей:

. (2.9)

Граничные условия IV-рода – условия сопряжения, сводятся к одновременному заданию температуры и тепловых потоков на границе раздела тел или фаз.

,

.

В дальнейшем: I рода – теплопроводность,

III рода – теплопередача.

2.3 Связь между правой декартовой, прямоугольной,

цилиндрической и сферической системами координат

Радиус-вектор r в цилиндрических координатах

, , , .

Радиус-вектор r в сферических координатах

, , , .

Тогда уравнение Лапласа в цилиндрических координатах будет иметь вид:

. (2.10)

В сферических:

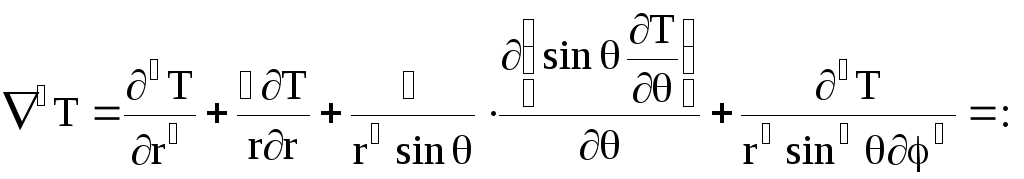. (2.11)

3. теплопроводность через плоскую

стенку при стационарном режиме

3.1 Теплопроводность через однослойную

плоскую стенку при граничных условиях I-го рода.

Т.к. процесс стационарный, то температуры на поверхности не меняются во времени и, следовательно,

,

и дифференциальное уравнение теплопроводности будет уравнение Лапласа. Так как температура меняется только вдоль оси ОХ, то для неё:

и .

В этом случае дифференциальное уравнение теплопроводности:

. (3.1)

При , температура ;

при , .

Решаем дифференциальное уравнение (3.1)

,  .

При , ;

при , ;

следовательно,

,

– решение ДУ (3.1). (3.2)

Формула (3.2) описывает распределение температуры в плоской однородной стенке.

Плотность теплового потока определяется согласно закону Фурье:

, (3.3)

Величина называется термическим сопротивлением

, . (3.4)

– тепловая проводимость.

– полный температурный перепад.

Текущий температурный перепад: .

Безразмерный температурный напор обозначим через

,

В безразмерных координатах Уравнение прямой линии имеет вид:

. (3.5)

Формула (3.5) – решение уравнения (3.1) в безразмерных координатах.

Чтобы найти тепловой поток Q надо по (3.3) определить плотность теплового потока и умножить её на поверхность:

Вт.

Количество теплоты, прошедшее через стенку

.