4 Перенос теплоты

через цилиндрическую стенку

4.1 Теплопроводность через цилиндрическую

однородную, однослойную стенку при граничных

условиях I-рода.

Ось OZ совмещаем с осью цилиндра, и температура меняется только вдоль радиуса цилиндра.

Для полого цилиндра заданы: внешний () и внутренний () радиусы, коэффициент теплопроводности (), температуры холодной и горячей стенок (и).

Требуется найти: уравнение, описывающее температурное поле в цилиндре, т.е. изменение температуры в зависимости от диаметра d (радиуса r), а также плотность теплового потока q и сам тепловой поток Q.

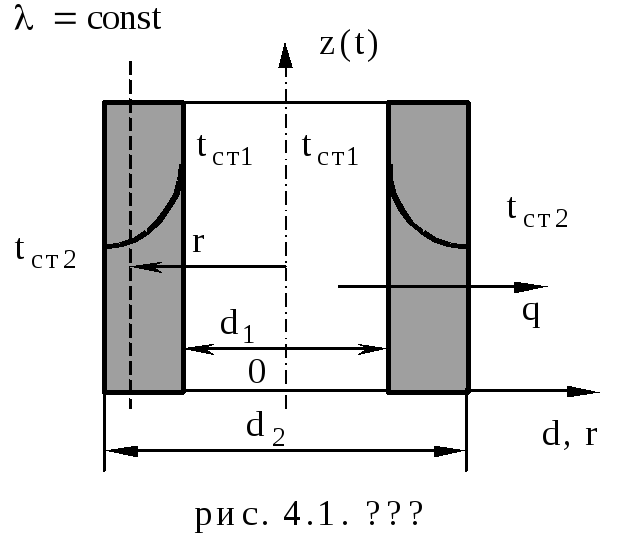
На основании дифференциального уравнения теплопроводности при стационарном режиме и отсутствии внутренних источников теплоты (2.10), учитывая, что первая и вторая производные температуры по z равны нулю

, ,

а также то, что температура не зависит от полярного угла , то уравнение Лапласа в цилиндрических координатах (2.10) упрощается до вида

. (4.1)

Граничные условия дифференциального уравнения:

при ;

при .

Введём новую переменную

,

тогда дифференциальное уравнение (4.1) будет иметь вид:

.

Интегрируем данное выражение:

.

Тогда, потенциируя это выражение и переходя к первоначальным переменным мы получаем:

.

После интегрирования получаем:

. (4.2)

Для определения постоянных интегрирования ивоспользуемся граничными условиями:

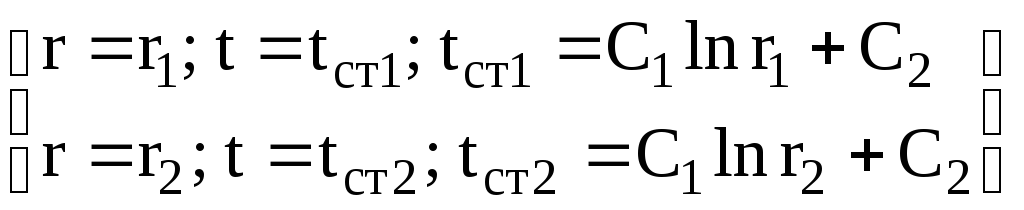(а)

Решая уравнение (а) относительно и, получаем

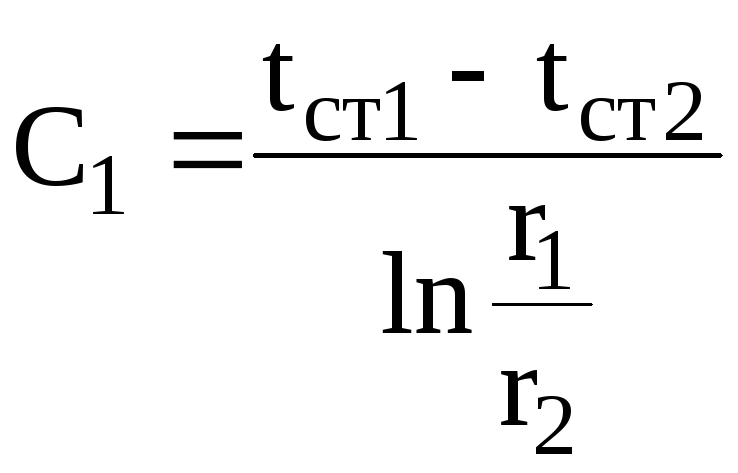, (б)

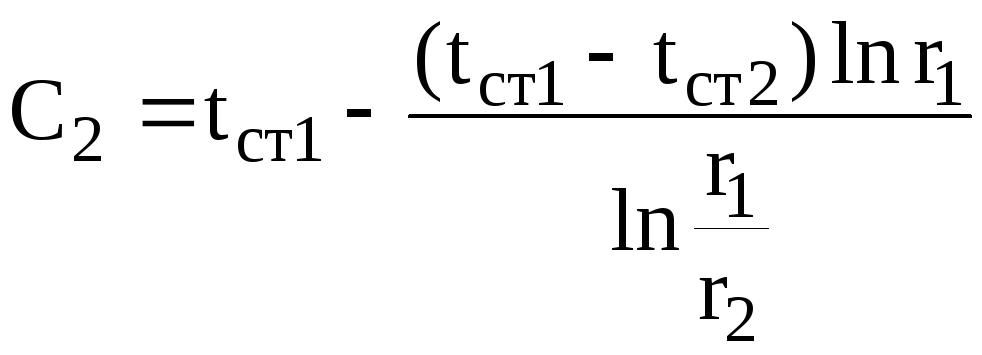, (с)

Подставляя в (4.2) значения и, получаем окончательное решение дифференциального уравнения

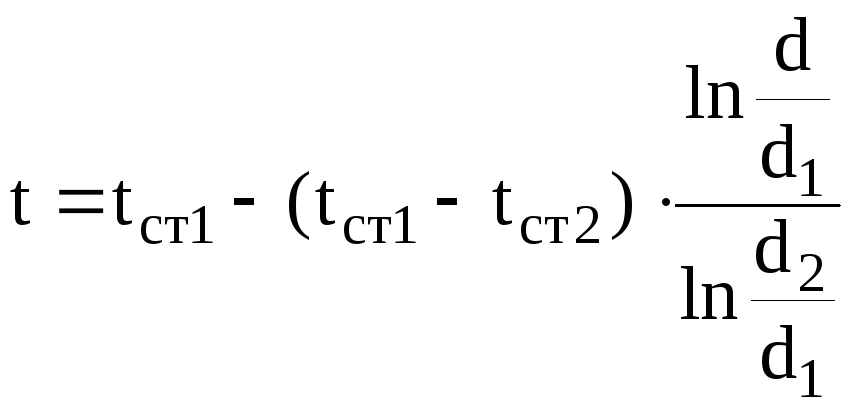. (4.3)

Это решение описывает распределение температуры в цилиндрической стенке. Это логарифмическая кривая (рис. 4.1). Задавая произвольным диаметр, можно определить температуру в любой точке цилиндрической поверхности.

Согласно закону Фурье плотность теплового потока пропорциональна градиенту температуры (температура меняется только вдоль радиуса):

;

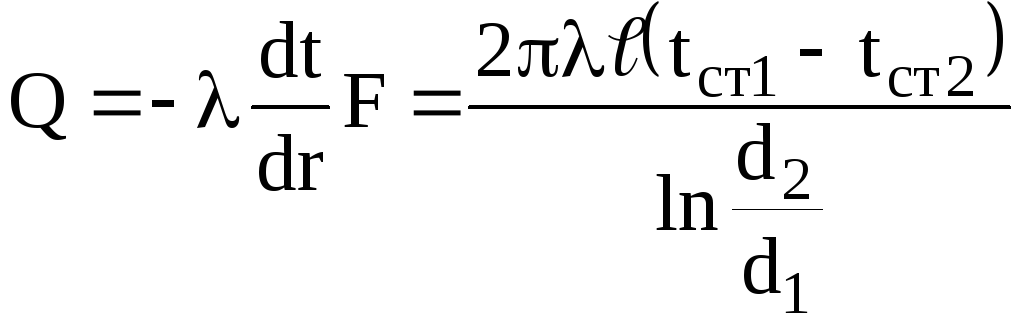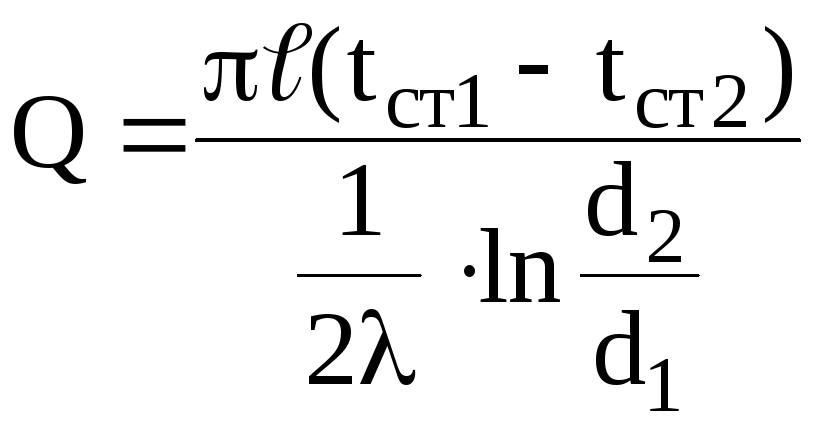, Вт. (4.4)

Из этого выражения следует, что тепловой поток полностью определяется внутренним и наружным диаметрами цилиндра (и).

Тепловой поток может быть отнесён к единице длины цилиндра

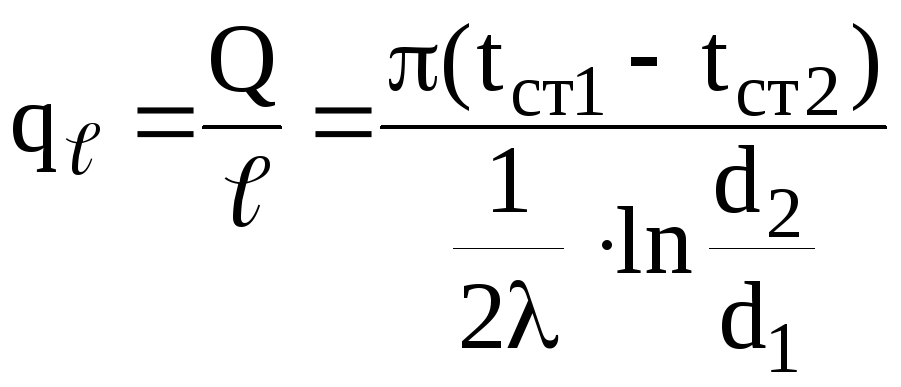,. (4.5)

(линейная плотность теплового потока) – это количество теплоты, проходящее через цилиндрическую поверхность путём теплопроводности через единицу длины

Тепловой поток может быть отнесён к внутренней поверхности цилиндра

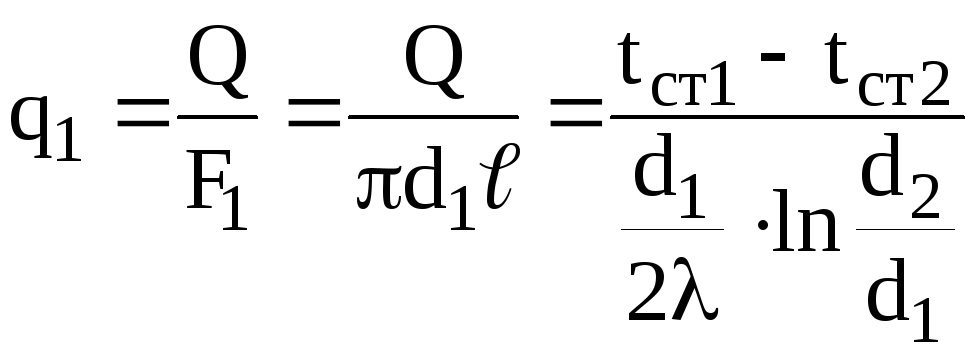,. (4.6)

Тепловой поток, отнесённый к наружной поверхности цилиндра

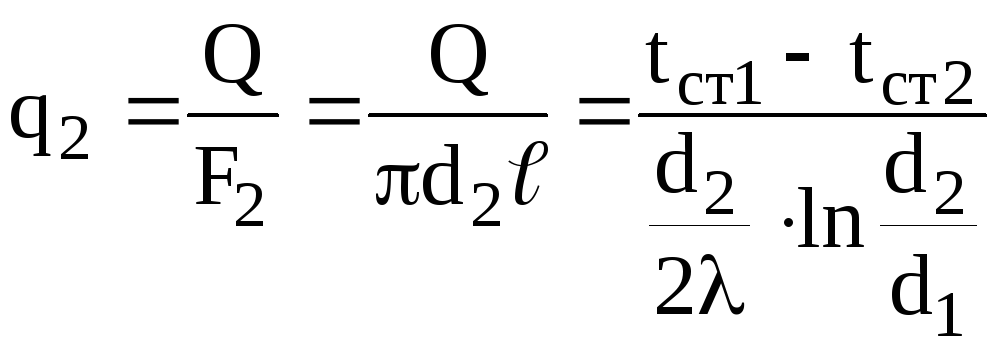,. (4.7)

Связь между различными приведёнными плотностями теплового потока следующая

, (4.8)

, т.к. .

Следовательно, в отличие от плоской стенки плотность теплового потока непостоянна по толщине цилиндрической стенки и определяется текущим диаметром цилиндра (чем больше текущий диаметр, тем меньше плотность теплового потока).

Если коэффициент теплопроводности не является величиной постоянной, а зависит от температуры по зависимости , то температурное поле, т.е. линии изменения температуры в цилиндрической стенке, на любом диаметре может быть определено из следующего выражения

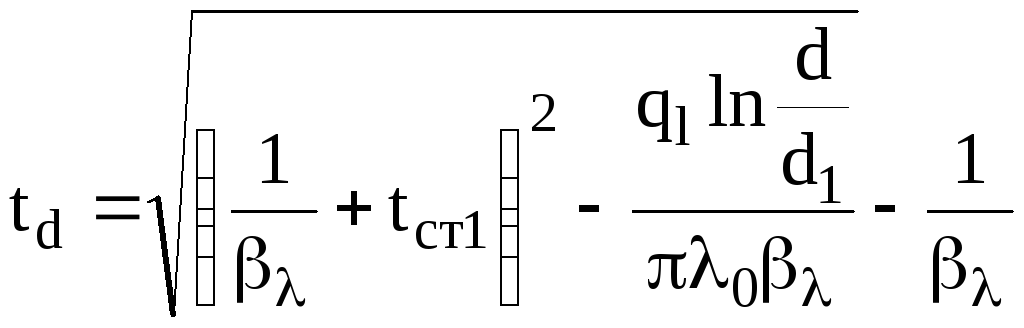. (4.9)

Подставляемые в выражение (4.9) значения иберутся из справочников.

4.2 Теплопередача через однослойную и многослойную цилиндрические стенки при граничных условиях III-рода

Для полого многослойного цилиндра заданы: температуры горячей и холодной жидкостей (и), внутренний и внешний диаметры (и), коэффициент теплопроводности (), коэффициенты теплоотдачи (и).

Требуется найти: тепловой поток (Q) и линейную плотность теплового потока () при передаче теплоты через однослойную и многослойную стенки.

Аналогично как для плоской стенки линейная плотность теплового потока будет отдаваться от горячей среды к внутренней поверхности цилиндра путём теплоотдачи. Эта же линейная плотность теплового потока будет проходить через цилиндрическую поверхность путём теплопроводности, и эта же линейная плотность теплового потока будет отдаваться от наружной поверхности цилиндра к холодной жидкости путём теплоотдачи (закон сохранения энергии). Запишем это математически:

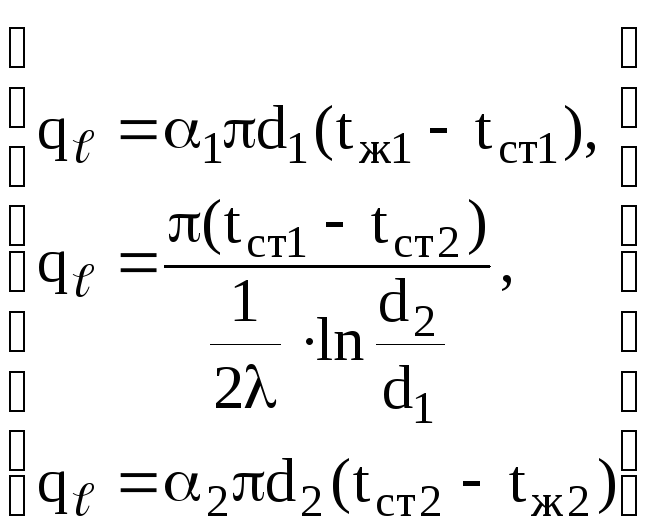(4.10)

Выразим из (4.10) разности температур и, сложив почленно эти три уравнения, получим:

,

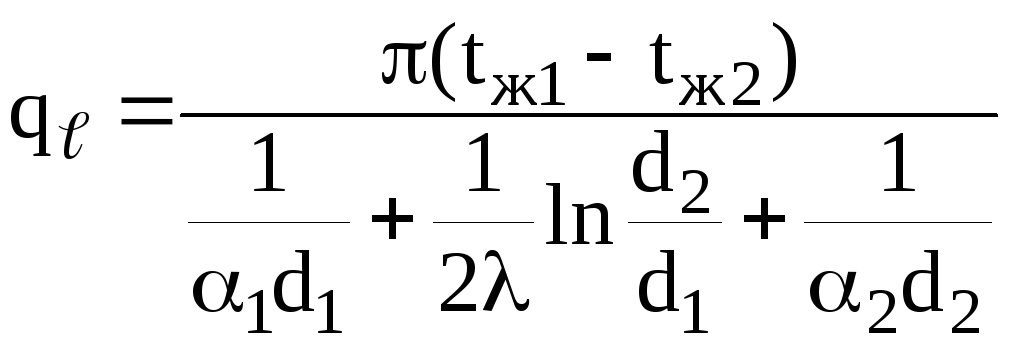,. (4.11)

Чтобы найти тепловой поток через цилиндрическую поверхность необходимо

, ,

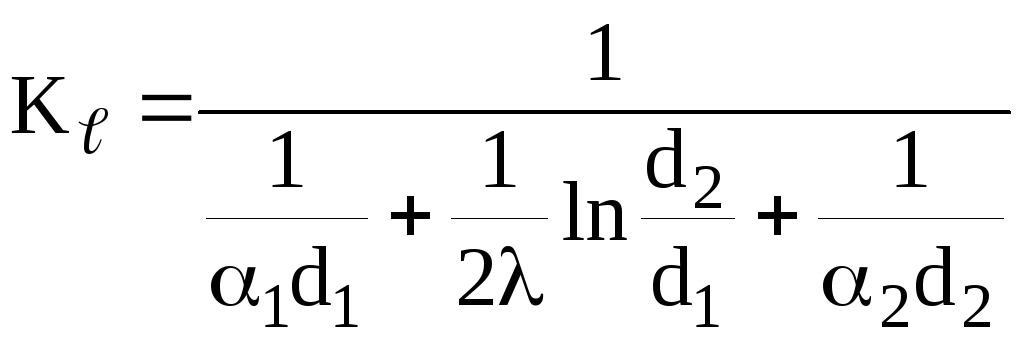,. (4.12)

(линейный коэффициент теплопередачи)

–это количество теплоты, передаваемое в единицу времени через единицу длины цилиндрической поверхности от одной среды к другой при разности температур между средами в 1 градус.

Величина обратная называется линейным термическим сопротивлением теплопередачи.

,. (4.12)

Плотность теплового потока, отнесённая к внутренней поверхности цилиндра, обозначим через

,

где – коэффициент теплопередачи через цилиндрическую стенку, отнесённый к внутренней поверхности цилиндра.

, .

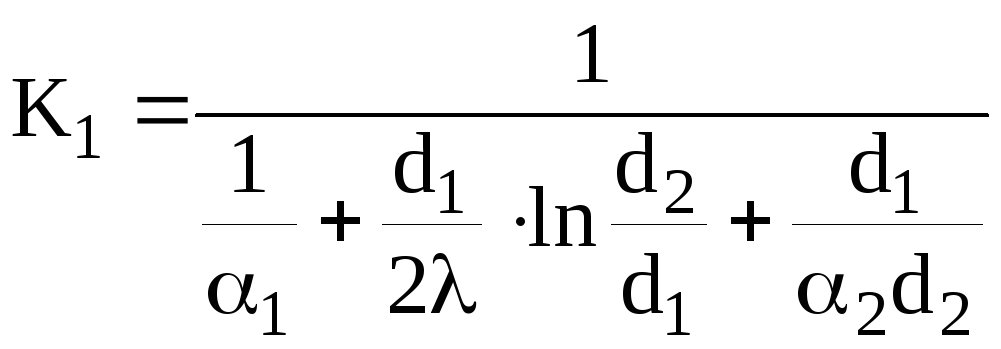Плотность теплового потока, отнесённая к внешней поверхности цилиндра, обозначим через

,

где – коэффициент теплопередачи через цилиндрическую стенку, отнесённый к внешней поверхности цилиндра.

.

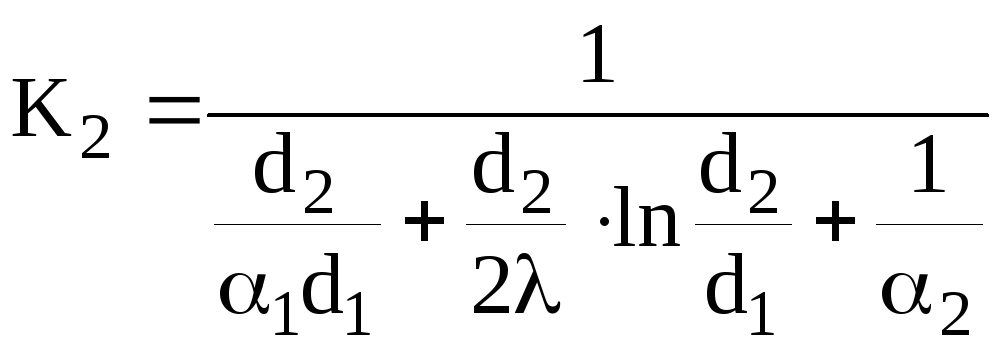Связь между коэффициентами теплопередачи следующая:

. (4.13)

Отсюда видно, что всегда, т.к..

На практике, если отношение наружного диаметра цилиндра к внутреннему не более 1.8, то можно пользоваться формулой расчёта коэффициента теплопередачи через плоскую стенку

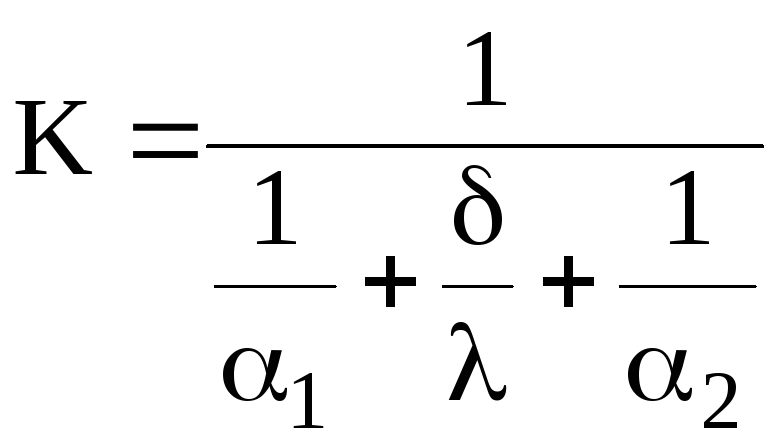
Тепловой поток для цилиндрической стенки рассчитывается:

, Вт.

В этом случае ошибка не превысит 4%. Если отношения диаметров больше 1.8, то следует использовать формулы для цилиндрической стенки.

Изоляцию трубопроводов рассчитывают как плоскую стенку. Ошибку можно уменьшить, если в качестве рассчётной брать поверхность со стороны меньшего .

1. Если , то;

2. если , то;

3. если , то.

Для многослойной цилиндрической стенки формула линейной плотности теплового потока имеет вид.

, .

где n – число слоёв.

Температура на границе раздела слоёв:

.