Lab_Electr / lab 10el

Цель работы:

• изучить движение заряженных частиц в электрическом и магнитных полях.

• определить удельный заряд электрона.

Теория

В электрическом поле на заряженную частицу, например, электрон, действует сила, пропорциональная величине заряда e и направленности поля Е

(1)

Под действием этой силы электрон, имеющий отрицательный заряд, перемещается в направлении, обратном направлению вектора (рис 1 a)

Пусть между плоскопараллельными пластинами приложена некоторая разность потенциалов U. Между пластинами создаётся однородное электрическое поле, напряжённость которого равна (2), где d – расстояние между пластинами.

Рассмотрим траекторию электрона, влетающего в однородное электрическое поле с некоторой скоростью (рис 1 б) .

Горизонтальная составляющая силы равна нулю, поэтому и составляющая скорости электрона остаётся постоянной и равна . Следовательно координата Х электрона определяется как

(3)

В вертикальном направлении под действием силы электрону сообщается некоторое ускорение , которое согласно второму закону Ньютона равно

(4)

Следовательно за время электрон приобретает вертикальную составляющую скорости (5)

Откуда .

Изменение координаты У электрона от времени получим, проинтегрировав последнее выражение:

(6)

Подставим значение t из (3) в (6) и получим уравнение движения электрона У (Х)

(7)

Выражение (7) представляет собой уравнение параболы.

Если длина пластин равна , то за время пролёта между пластинами электрон приобретает горизонтальную составляющую

(8)

из (рис 1 б) следует, что тангенс угла отклонения электрона равен

(9)

Таким образом, смещение электрона, как и любой другой заряженной частицы, в электрическом поле пропорционально напряжённости электрического поля и зависит от величины удельного заряда частицы е/m.

Движение заряженных частиц в магнитном поле

Рассмотрим теперь траекторию электрона , влетающего в однородное магнитное поле со скоростью (рис.2)

Магнитное поле воздействует на электрон с силой F_л , величина которой определяется соотношением Лоренца

(10)

или в скалярном виде

(11)

где В – индукция магнитного поля;

 - угол между векторами и . Направление силы Лоренца определяется по правилу левой руки с учётом знака заряда частицы.

Отметим, что сила, действующая на электрон, всегда перпендикулярна вектору скорости и, следовательно, является центростремительной силой. В однородном магнитном поле под действием центростремительной силы электрон будет двигаться по окружности радиуса R. Если электрон движется прямолинейно вдоль силовых линий магнитного поля, т.е. =0, то сила Лоренца F_л равна нулю и электрон проходит магнитное поле, не меняя направления движения. Если вектор скорости перпендикулярен вектору , то сила действия магнитного поля на электрон максимальна

(12)

Так как сила Лоренца является центростремительной силой, то можно записать: , откуда радиус окружности, по которой движется электрон, равен:

(13)

Более сложную траекторию описывает электрон, влетающий в магнитное поле со скоростью под некоторым углом  к вектору (рис.3). В этом случае скорость электрона имеет нормальную и тангенциальную составляющие. Первая из них вызвана действием силы Лоренца, вторая обусловлена движением электрона по инерции. В результате электрон движется по цилиндрической спирали. Период его обращения равен (14) , а частота (15). Подставим значение R из (13) в (15):

Из последнего выражения следует, что частота обращения электрона не зависит ни от величины, ни от направления его начальной скорости и определяется только величинами удельного заряда и магнитного поля. Это обстоятельство используется для фокусировки электронных пучков в электронно-лучевых приборах. Действительно, если в магнитном поле попадает пучок электронов, содержащий частицы с различными скоростями (рис.4), то все они опишут спираль разного радиуса, но встретятся в одной и той же точке согласно уравнению (16). Принцип магнитной фокусировки электронного пучка и лежит в основе одного из методов определения е/m. Зная величину В и измерив частоту обращения электронов , по формуле (16) легко вычислить значение удельного заряда.

Если зона действия магнитного поля ограничена, а скорость электрона достаточно велика, то электрон движется по дуге и вылетает из магнитного поля, изменив направление своего движения (рис 5). Угол отклонения  рассчитывается так же, как и для электрического поля и равен: , (17) где в данном случае – протяжённость зоны действия магнитного поля. Таким образом, отклонение электрона в магнитном поле пропорционально е/m и В и обратно пропорционально .

В скрещенных электрическом и магнитном полях отклонение электрона зависит от направления векторов и и соотношения их модулей. На рис. 6 электрическое и магнитное поля взаимно перпендикулярны и направлены таким образом, что первое из них стремиться отклонить электрон вверх, а второе – вниз. Направление отклонения зависит от соотношения сил F_л и . Очевидно, что при равенстве сил и F_л (18) электрон не изменит направления своего движения.

Предположим, что под действием магнитного поля электрон отклонился на некоторый угол . Затем приложим электрическое поле некой величины, чтобы смещение оказалось равным нулю. Найдём из условия равенства сил (18) скорость и подставим её значение в уравнение (17).

Откуда

(19)

Таким образом зная угол отклонения , вызванный магнитным полем , и величину электрического поля , компенсирующую это отклонение, можно определить величину удельного заряда электрона е/m .

Определение удельного заряда методом магнетрона.

Определение е/m в скрещенных электрическом и магнитном полях может быть выполнено также с помощью двухэлектродного электровакуумного прибора – диода. Этот метод известен в физике, как метод магнетрона. Название метода связано с тем, что используемая в диоде конфигурация электрического и магнитного полей идентична конфигурации полей в магнетронах – приборах, используемых для генерации электромагнитных колебаний в СВЧ - области.

Между цилиндрическим анодом А и цилиндрическим катодом К (рис.7), расположенным вдоль анода, приложена некоторая разность потенциалов U , создающая электрическое поле E, направленное по радиусу от анода к катоду. В отсутствие магнитного поля (В=0) электроны движутся прямолинейно от катода к аноду.

П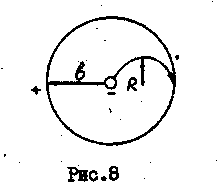ри наложении слабого магнитного поля, направление которого параллельно оси электродов, траектория электронов искривляется под действием силы Лоренца, но они достигают анода. При некотором критическом значении индукции магнитного поля В=В_кр, траектория электронов искривляется настолько, что в момент достижения электронами анода вектор их скорости направлен по касательной к аноду. И, наконец, при достаточно сильном магнитном поле В>В_кр, электроны не попадают на анод. Значение В_кр не является постоянной величиной для данного прибора и зависит от величины приложенной между анодом и катодом разности потенциалов.

Точный расчёт траектории движения электронов в магнетроне сложен, так как электрон движется в неоднородном радиальном электрическом поле. Однако, если радиус катода много меньше радиуса анода b, то электрон описывает траекторию, близкую к круговой, так как напряжённость электрического поля, ускоряющего электроны, будет максимальной в узкой прикатодной области. При В=В_кр радиус круговой траектории электрона, как видно из рис.8. будет равен половине радиуса анода R=b/2. Следовательно, согласно (13) для В_кр имеем:

(20)

С другой стороны кинетическая энергия электронов, находящихся вблизи анода, определяется только разностью потенциалов между анодом и катодом, так как в магнитном поле скорость не изменяется по величине. Тогда , откуда

(21)

Подставив значение из (20) в (21), получи выражение для расчёта удельного заряда электрона:

(22)

Таким образом, для определения удельного заряда электрона методом магнетрона, достаточно измерить анодную разность потенциалов U , критическое значение индукции магнитного поля В_кр и радиус анода b.