физика лекцыи_1 / 1

1.9. КИНЕМАТИКА ДВИЖЕНИЯ ТВЕРДОГО ТЕЛА

Понятие твердого тела. Число степеней свободы абсолютно твердого тела. Поступательное и вращательное движения твердого тела. Угловая скорость и угловое ускорение. Вектор угловой скорости при вращательном движении. Векторные соотношения между угловыми и линейными величинами, характеризующими движение.

Следующей по сложности моделью после частицы является абсолютно твердое тело.     Абсолютно твердое тело — тело деформацией которого в условиях данной задачи можно пренебречь и расстояние между любыми двумя точками этого тела остается постоянным. Описание движения твердого тела кроме самостоятельного значения имеет большое значение и в применении к описаниям других видов движения. Система отсчета, служащая для пространственно-временного описания различных движений может быть связана только с твердым телом. Поэтому изучение движения твердых тел равносильно изучению движений систем отсчета. Результаты этого раздела будут неоднократно использоваться в дальнейшем.

Количество независимых величин, которые необходимо задать, чтобы определить положение тела в пространстве, называется числом степеней свободы тела. Для определения положения в пространстве материальной точки нужно задать три координаты (x, у, z) число степеней свободы равно трем. Две материальные точки (N=2), связанные между собой (n=1) имеют 5 степеней свободы 3+3 – 1 или 3N-n В общем случае для твердого тела 6 степеней свободы 3+3+3-3=6. Если тело состоит из 3-х точек (x₁,y₁,z₁), (x₂,y₂,z₂), (x₃,y₃,z₃).

    

 Имеется пять видов движения твердого тела:

1)поступательное, при котором прямая, соединяющая любые две точки тела, перемещается, оставаясь параллельной своему начальному положению, например движение трамвая на прямом участке пути;

2) вращательное, при котором все точки тела описывают окружности, расположенные в параллельных плоскостях. Центры всех окружностей лежат при этом на одной прямой, перпендикулярной к плоскостям окружностей и называемой осью вращения. Ось вращения может располагаться внутри тела и за его пределами. Ось вращения в данной системе отсчёта может быть как подвижной, так и неподвижной.

3) плоское, при котором все точки тела движутся в плоскостях, параллельных некоторой плоскости, неподвижной в рассматриваемой системе отсчета, например качение колеса на прямом участке пути;

4)сферическое, при котором одна из точек тела остается все время неподвижной в рассматриваемой системе отсчета, например движение гироскопа с тремя степенями свободы в карданном подвесе;

5)свободное, если нет перечисленных выше четырех ограничений, например движение свободного произвольного брошенного тела вблизи поверхности Земли.

     

Первые два движения являются основными движениями твердого тела. Остальные виды движения твердого тела можно свести к одному из основных движений или к их совокупности.

     

 При поступательном движении все точки твердого тела совершают равные перемещения за один и тот же промежуток времени. Поэтому скорости и ускорения всех точек тела в данный момент времени одинаковы. Этот факт позволяет свести изучение поступательного движения твердого тела к изучению движения отдельной частицы тела, т. е. к задаче кинематики частицы. Таким образом, поступательное движение твердого тела может быть полностью описано, если известны зависимость от времени радиус-вектора любой точки этого тела и его положение в начальный момент.

     

Рассмотрим вращение вокруг неподвижной в данной системе отсчета

Рис. 9.1. Вращение твердого тела вокруг неподвижной оси

 оси 00'. Пусть твердое тело, вращаясь вокруг нее, совершило за время dt бесконечно малый поворот. Угол поворота будем характеризовать вектором , модуль которого равен углу поворота , а направление совпадает с осью 00', причем так, что направление поворота отвечает правилу правого винта по отношению к направлению вектора (рис. 9.1). Вектор называется аксиальным вектором, тогда как вектор перемещения является полярным вектором (к ним также относятся векторы скорости и ускорения). Они отличаются тем, что полярный вектор кроме длины и направления имеет точку приложения (полюс), а аксиальный вектор имеет только длину и направление (ось - по латыни axis), но не имеет точки приложения. Векторы такого типа часто применяются в физике. К ним, например, относятся все векторы, являющиеся векторным произведением двух полярных векторов.

     

Найдем элементарное перемещение любой частицы А твердого тела при таком повороте. Положение частицы А зададим радиус-вектором , проведенным из некоторой точки О на оси вращения. Тогда линейное перемещение конца радиус-вектора связано с углом поворота соотношением (рис. 2.6)

     

     или в векторном виде

     

(9.1)

     Заметим, что это равенство справедливо лишь для бесконечно малого поворота , то есть только бесконечно малые повороты можно рассматривать как векторы. Для конечного поворота на угол линейное перемещение частицы А определяется формулой

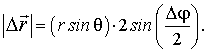
     Очевидно, что перемещение нельзя представить как векторное произведение векторов и , так как это возможно лишь при бесконечно малом повороте , когда радиус-вектор можно считать неизменным.

     Можно показать, что введенный вектор удовлетворяет основному свойству векторов - векторному сложению. Пусть твердое тело совершает два элементарных поворота ₁ и ₂ вокруг разных осей, проходящих через неподвижную точку О. Тогда суммарное перемещение произвольной частицы А тела, радиус-вектор которой относительно точки О равен , можно представить так:

     

,

     где

     

(9.2)

     

Таким образом, два поворота, ₁ и ₂, эквивалентны одному повороту на угол вокруг оси, совпадающей с вектором и проходящей через точку О.

    

 Введем теперь векторы угловой скорости и углового ускорения таким же способом, как мы вводили векторы и . Вектор угловой скорости определяют так

     

,

(9.3)

где dt - интервал времени, за который тело совершает поворот . Вектор совпадает по направлению с вектором и является аксиальным вектором.

     

Изменение вектора со временем характеризуют вектором углового ускорения , который определяют соотношением

     

,

(9.4)

Направление вектора совпадает с направлением - приращения угловой скорости . Вектор , как и , также аксиальный.

     

Представление угловой скорости и углового ускорения в виде векторов очень полезно при изучении более сложных движений твердого тела. Это позволяет во многих случаях получить большую наглядность, а также резко упростить как анализ движения, так и соответствующие расчеты.

     

Представим выражения для угловой скорости и углового ускорения в проекциях на ось вращения Оz, положительное направление которой свяжем правилом правого винта с положительным направлением отсчета координаты -угла поворота- (рис. 9.2).

Рис. 9.2. Введение понятия угловых векторов

Тогда проекции и векторов и на ось определяются формулами:

     

(9.5)

     

(9.6)

    

В этих формулах и - алгебраические величины. Их знак характеризует направление соответствующего вектора. Например, если , то направление вектора совпадает с положительным направлением оси z. Если , то и направление вектора противоположно. Аналогично правило верно для углового ускорения.

     

По известной зависимости , называющейся законом вращения тела, формулы (9.5) и (9.6) дают возможность определить угловую скорость и угловое ускорение в любой момент времени. Из зависимости углового ускорения от времени и начальных условий, т. е. угловой скорости и угла (₀ в начальный момент времени, можно найти и .

     

Пусть твердое тело вращается вокруг неподвижной оси по закону , где и - некоторые положительные постоянные. Определим движения тела.

Согласно (2.15) и (2.16), . Из этих соотношений видно, что тело вращается равнозамедленно (), останавливается в момент времени , а затем начинает вращаться в противоположном направлении ().

     

Все задачи на вращение твердого тела вокруг неподвижной оси аналогичны по форме задачам на прямолинейное движение частицы. Достаточно заменить линейные величины x, и на соответствующие угловые , и , как получаются все закономерности и соотношения для вращающегося тела.

     

Установим связь между линейными и угловыми величинами.

Рис. 9.3. Связь линейных и угловых величин при вращении

     

Определим вектор скорости произвольной частицы А твердого тела, вращающегося вокруг неподвижной оси 00' с угловой скоростью . Пусть положение точки А относительно некоторой точки О оси вращения характеризуется радиус-вектором (рис. 9.3).

     

Если формулу (9.1) поделить на промежуток времени dt, то так как и ), получим

     

(9.7)

т. е. скорость любой частицы А твердого тела, вращающегося вокруг некоторой оси с угловой скоростью , равна векторному произведению на радиус-вектор частицы А относительно произвольной точки О оси вращения (рис. 9.3). Модуль вектора (9.7), или , где R- радиус окружности, по которой движется точка А. Дифференцирование равенства (9.7) по времени дает ускорение частицы А: , т.е.

     

.

(9.8)

Так как в рассматриваемом случае ось вращения неподвижна, то угловая скорость параллельна угловому ускорению, поэтому первое слагаемое в (9.8) представляет собой тангенциальное ускорение , а второе слагаемое - это нормальное ускорение . Модули этих ускорений равны: , отсюда модуль полного ускорения a равен .

     

7