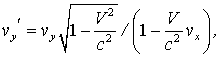физика лекцыи_1 / 1.16

1.16. ПОСТУЛАТЫ СПЕЦИАЛЬНОЙ ТЕОРИИ ОТНОСИТЕЛЬНОСТИ

Принцип относительности в механике. Преобразования Галилея. Законы сохранения и симметрия пространства-времени. Границы применимости преобразований Галилея. Постулаты специальной теории относительности. Преобразования Лоренца. Взаимосвязь пространства и времени. Относительность длин и промежутков времени. Закон сложения скоростей в специальной теории относительности.

В классической механике при скоростях тел значительно меньших, чем скорость света (c << υ) справедлив механический принцип относительности. Он составляет сущность принципа относительности Галилея. Принцип относительности Галилея: законы динамики одинаковы во всех инерциальных системах отсчета. Основные постулаты и противоречия классической механики: 1. Физическое пространство однородно и изотропно. Пространство и время существуют сами по себе и независимо от материальных тел. (При затмении Солнца наблюдалось отклонение солнечных лучей от прямолинейного распространения (кривизна пространства)). 2. Все механически явления протекают одинаково в любой инерциальной системе отсчета. 3. Взаимодействие между физическим объектами происходит мгновенно т.е.скорость взаимодействия бесконечно большая. ( Скорость света не зависит от системы координат и является предельной). 4. Масса материальной точки не зависит от скорости движения. (Масса частиц зависит от скорости). 5. Все кинематические характеристики можно измерить сколь угодно точно. (Выполняются соотношения неопределенностей). Преобразования Галилея. Рассмотрим две системы отсчета: инерциальную систему К (с координатами x, y, z), условно будем считать неподвижной, и систему К' (с координатами x', y', z'), движущуюся относительно К равномерно и прямолинейно со скоростью υ0 (υ0=const) Координата точки А по отношению к системе К: х = х' + 00', за промежуток времени t от начала отсчета будет: (16.1) Уравнения (16.1) носят название преобразования координат и времени Галилея. Отсчет времени начат с момента, когда начало координат обеих систем совпадают. Продифференцировав по времени t, получим выражение правила сложения скоростей в классической механике: υ=υ'+υ0 (16.2) Ускорения в обеих системах отсчета одинаковы, а это означает, что поведение тел в обеих системах одинаково: a=a' (16.3), т.е. из соотношения (16.3) вытекает подтверждение механического принципа относительности: уравнения динамики при переходе от одной инерциальной системы отсчета к другой не изменяются, т.е. являются инвариантными по отношению к преобразованиям Галилея. Механический принцип относительности можно сформулировать еще следующим образом: никакими механическими опытами, проведенными в данной инерциальной системе отсчета, нельзя установить, покоится ли она или движется равномерно и прямолинейно. Например, сидя в каюте корабля, движущегося равномерно и прямолинейно, мы не можем определить, покоится корабль или движется, не выглянув в окно.

Рассмотрим основные положения, связывающие инвариантность каких либо физических величин с законами сохранения.

Инвариантность - неизменность какой-либо величины при изменении физических условий или по отношению к некоторым преобразованиям, напр., преобразованиям координат и времени при переходе от одной инерциальной системы отсчета к другой (релятивистская инвариантность).

Симметрия (от греч. symmetria — соразмерность) - в широком смысле — инвариантность (неизменность) структуры, свойств, формы материального объекта относительно его преобразований (т. е. изменений ряда физических условий). Симметрия лежит в основе законов сохранения.

Весьма важным для понимания законов природы является принцип инвариантности относительно сдвигов в пространстве и во времени, т. е. параллельных переносов начала координат и начала отсчета времени. Он формулируется так: смещение во времени и в пространстве не влияет на протекание физических процессов.

Инвариантность непосредственно связана с симметрией, представляющей собой неизменность структуры материального объекта относительно его преобразований, т. е. изменения ряда физических условий.

В широком смысле симметрия означает инвариантность как неизменность свойств системы при некотором изменении (преобразовании) ее параметров.

Из сформулированного принципа инвариантности относи­тельно сдвигов в пространстве и во времени следует симметрия пространства и времени, называемая однородностью простран­ства и времени.

В предыдущих разделах рассмотрены три фундаментальных закона природы: закон сохранения импульса, момента импульса и энергии. Следует понимать, что эти законы выполняются только в инерциальных системах отсчета.В самом деле, при выводе этих законов мы пользовались вторым и третьим законами Ньютона, а они применимы только в инерциальных системах. Напомним также, что импульс и момент импульса сохраняются в том случае, если система замкнутая (сумма всех внешних сил и всех моментов сил равна нулю). Для сохранения же энергии тела условия замкнутости недостаточно – тело должно быть еще и адиабатически изолированным (т.е. не участвовать в теплообмене). Во всей истории развития физики законы сохранения оказались чуть ли не единственными законами, сохранившими свое значение при замене одних теорий другими. Эти законы тесно связаны с основными свойствами пространства и времени.

В основе закона сохранения энергии лежит однородность времени, т. е. равнозначность всех моментов времени (симметрия по отношению к сдвигу начала отсчета времени). Равнозначность следует понимать в том смысле, что замена момента времени t₁ на момент времени t₂, без изменения значений координат и скорости частиц, не изменяет механические свойства системы. Это означает то, что после указанной замены, координаты и скорости частиц имеют в любой момент времени t₂ + t такие же значения, какие имели до замены, в момент времени t₁ + t. Другими словами, однородность времени означает инвариантность физических законов относительно выбора начала отсчета времени. Напри­мер, при свободном падении тела в поле силы тяжести его ско­рость и пройденный путь зависят лишь от начальной скорости и продолжительности свободного падения тела и не зависят от того, когда тело начало падать.

В основе закона сохранения импульса лежит однородность пространства, т. е. одинаковость свойств пространства во всех точках (симметрия по отношению к сдвигу начала координат). Одинаковость следует понимать в том смысле, что параллельный перенос замкнутой системы из одного места пространства в другое, без изменения взаимного расположения и скоростей частиц, не изменяет механические свойства системы, иными словами, не зависят от выбора положения начала координат инерциальной системы отсчета.

В основе закона сохранения момента импульса лежит изотропия пространства, т. е. одинаковость свойств пространства по всем направлениям (симметрия по отношению к повороту осей координат). Одинаковость следует понимать в том смысле, что поворот замкнутой системы, как целого, не отражается на её механических свойствах. Между законами типа основного уравнения динамики и законами сохранения имеется принципиальная разница. Законы динамики дают нам представление о детальном ходе процесса. Так, если задана сила, действующая на материальную точку и начальные условия, то можно найти закон движения, траекторию, величину и направление скорости в любой момент времени и т. п. Законы же сохранения не дают нам прямых указаний на то, как должен идти тот или иной процесс. Они говорят лишь о том, какие процессы запрещены и потому в природе не происходят.

Таким образом, законы сохранения проявляются как принципы запрета: любое явление, при котором не выполняется хотя бы один из законов сохранения, запрещено, и в природе такие явления никогда не наблюдаются. Всякое явление, при котором не нарушается ни один из законов сохранения, в принципе может происходить.

Специальная теория относительности (СТО) давно стала наукой прикладной, широко используемой в современной инженерной практике. Достаточно указать на расчеты при проектировании ускорителей элементарных частиц, атомных реакторов, на вычисление энергетических выходов различных ядерных реакций и многое другое.

Возникла СТО после триумфального, более чем двухсотлетнего развития классической физики, когда в конце XIX века неожиданно обнаружилось несовершенство физической теории как в теоретическом, так и в прикладном аспектах. В теоретическом - противоречие между структурами электродинамики Максвелла и механики Ньютона (отсутствие основополагающего принципа относительности в электродинамике при наличии его в механике). В прикладном - невозможность объяснить ряд новооткрытых фактов -опыт Майкельсона (попытка обнаружить движение Земли относительно светоносного эфира - особой упругой среды, возмущения которой представляют собой поперечные электромагнитные волны), опыт Физо (измерение скорости распространения света в движущейся воде с целью обнаружить увлечение ей светоносного эфира), аберрация света, действие униполярных машин, непрерывное излучение энергии радиоактивными элементами без заметного их изменения, позже - распад мезонов при больших скоростях и многое другое.

     

СТО строится для инерциальных систем отсчета (ИСО) - систем, по отношению к которым выполняется закон инерции. ИСО относится к числу научных абстракций, идеальных моделей. Как известно, вся физика вообще строится на научных абстракциях, моделях (простейшие из них: материальная точка (частица), абсолютно твердое тело, идеальный газ, идеальная жидкость, точечный заряд, упругое тело и т.д.). Метод идеализации (моделей) открывает широкие возможности для использования математического анализа и в то же время не ставит преград для приложения теории к реальным объектам и явлениям, поскольку модели постоянно совершенствуются.

     

Реально существуют лишь прототипы инерциальных систем отсчета, связанные с конкретными телами (с Землей, с Солнцем, с космическим кораблем, с поездом, с лабораторией исследователя и т.п.). Если движение исследуемого объекта относительно некоторой конкретной системы отсчета описывается ньютоновой механикой с достаточной для практики степенью точности, то такую систему отсчета обычно и считают инерциальной. Важно, что закон инерции (первый закон Ньютона) гарантирует существование инерциальной системы отсчета в указанном смысле для любой предложенной задачи механики. Нередко система отсчета, связанная с каким-либо конкретным телом проявляет себя как инерциальная для одной задачи, и в то же время оказывается неинерциальной для другой,

     

В классической механике пространство и время абсолютны - одинаковы во всех системах отсчета вообще.

     

В специальной теории относительности предполагается, что в одной отдельно взятой ИСО метрические свойства пространства и времени такие как в классической механике. Именно, пространство отдельно взятой ИСО евклидово (теорема Пифагора), трехмерное, однородное, изотропное, непрерывное, односвязное. Время одномерное, однородное, непрерывное, однонаправленное. Все эти качества являются следствием многовековой практики человечества.

В основе специальной теории относительности А. Эйнштейна лежат два постулата, смысл которых можно выразить так:

 1. При одинаковых условиях, реализованных по отдельности в двух системах отсчета - некоторой инерциальной системы К и системы К', движущейся равномерно и прямолинейно относительно системы I - любые физические процессы в этих системах отсчета протекают одинаково. Или все физические явления во всех инерциальных системах отсчёта описываются одинаковыми закономерностями.

     

2. В природе существует предельная (максимальная) скорость распространения физических сигналов (взаимодействий), одна и та же во всех инерциальных системах отсчета. Эта максимальная скорость совпадает со скоростью света в вакууме, она не зависит от движения источника и приемника света и равна с = 300000 км/с .

     

Из первого принципа следует: если для данной задачи (некоторого класса задач) найдена инерциальная система отсчета I, то для этой задачи существует и бесчисленное множество инерциальных систем типа II, движущихся равномерно прямолинейно относительно I. Скорости всех систем II меньше с. Системы отсчета необходимо связывать с телами, а скорости тел не могут равняться или превосходить максимальную скорость света в вакууме, равную с. Скорости тел строго меньше максимальной.

     

Развитие науки показало, что оба принципа Эйнштейна подтверждаются всей совокупностью экспериментальных и теоретических знаний современной физики.

     

Из принципов Эйнштейна следует: одновременность разноместных событий не является абсолютной, независимой от систем отсчета.

     

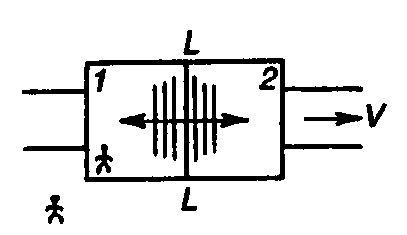
Действительно, пусть от лампы L, находящейся на середине платформы, движущейся со скоростью V, начал распространяться свет.

     .

Рис.16.1 Относительность одновременности разноместных событий

     

Для наблюдателя, находящегося на платформе, свет дойдет до ее концов одновременно, тогда как для наблюдателя на перроне он дойдет до левого конца раньше, а до правого позже, т.к. левый конец приближается к фронту световой волны, а правый отдаляется (оба наблюдателя исходят из принципов Эйнштейна; скорость света в обоих направлениях для каждого из наблюдателей равна максимальной скорости с и не зависит от того движется или покоится источник света).

     

Математическое описание физических явлений требует использования системы отсчета, а значит установления взаимно однозначного соответствия между моментами времени и числами, а также между точками пространства и тройками чисел (координатами точек) в различных системах отсчета.   В дальнейшем рассмотрении две инерциальные системы отсчета будем обозначать система I и система II и считать их движущимися друг относительно друга так, как это показано на (рис. 7.2).

Рис.16.2. Взаимное расположение двух движущихся инерциальных систем отсчета

В итоге, с каждой из систем I и II связаны неподвижные в этих системах часы. Часы системы II движутся относительно часов системы I со скоростью V, Здесь и всегда дальше предполагается, что система II движется со скоростью относительно системы I в направлении оси абсцисс Х. Остается только согласовать выбор начал отсчета времени в системах 1 и II между собой. Принимается условие: когда декартовы оси обеих систем I и II совмещались, часы начал координат в обеих системах должны были показывать одинаковое время: t = 0 (в системе I) и также t = 0 (в системе П).

     

Связь между координатами и временем какого-либо события в системе I и соответствующими параметрами в системе II определяется преобразованиями Лоренца. Физический процесс - это последовательность событий. Событие определяется местом (координатами), где оно произошло, и моментом времени, когда оно произошло. Пусть координаты некоторого события в системе отсчета I равны , а в системе II они . Связь между ними находяться, исходя из принципов Эйнштейна. А именно 

     

(16.4)

     

Такова связь между координатами (включая время) одного и того же события в двух инерциальных системах отсчета I и II (штрихованная система 1 движется относительной не штрихованной I со скоростью V в направлении оси х). Преобразования Лоренца (релятивистские преобразования) устанавливают взаимосвязь пространства и времени — в закон преобразования координат входит время, а в закон преобразования времени — пространственные координаты.

Из формул (16.4) в частности следует: одновременные, но происходящие в разных точках пространства, события в системе I не являются таковыми в системе II. Действительно, если , то для одного и того же t имеем

     

     то есть .

     

Если разрешить равенства (16.4) относительно не штрихованных координат (это означает переход II >I), то получим

     

(16.5)

     

Эти формулы отличаются от (16.4) только тем, что штрихованные и не штрихованные координаты поменялись местами, а скорость (+V) заменена на (- V), что вполне понятно - системы I и II равноправны и I движется относительно II со скоростью (- V).

     Если , то формулы (16.4) преобразований Лоренца вырождаются и принимают вид

     

     

Это известные в ньютоновой механике преобразования Галилея. С ними связано представление об абсолютном времени, одинаково текущем во всех системах отсчета (одновременность событий абсолютна - относится ко всем системам отсчета).

     

Преобразования Лоренца знаменуют в науке новый этап в познании метрических свойств пространства и времени, более глубоких, чем те, которые сложились постепенно в грубом человеческом опыте и отражены в ньютоновой механике. Неудивительно поэтому, что из преобразований Лоренца вытекают кинематические следствия, которые не согласуются со "здравым смыслом". Рассмотрим два основных из них.

     

Рассмотрим линейку, неподвижную в I, размещенную параллельно оси абсцисс. Длина линейки , где и - координаты концов линейки в этой системе I.

     

В системе II длина этой линейки , где и следует брать в один и тот же момент . По преобразованию Лоренца

     

     

Вычитая, находим

     

     

Длина предмета в системе отсчета, в которой он покоится, называется собственной длиной (здесь - ). Она наибольшая. В системе, относительно которой линейка движется, она короче , и тем короче, чем больше ее скорость V. Следовательно, длина не является понятием абсолютным (безотносительным к системам отсчета), как принимается в ньютоновой механике. Таким образом, размер тела, движущегося относительно инерциальной системы отсчета, уменьшается в направлении движения, причем лоренцово сокращение длины тем больше, чем больше скорость движения. Поперечные размеры тел не зависят от скорости его движения и одинаковы во всех инерциальных системах отсчета.

     

Пусть в неподвижной точке системы II произошли два события: первое - в момент , второе - в момент . Промежуток времени между этими событиями . По формулам Лоренца

     

Вычитая значения моментов времени , находим

     

     

Видно, что здесь больше, чем . В системе отсчета, в которой часы покоятся, промежуток времени наименьший. Его называют собственным временем. Иногда этот результат выражают словами: в движущемся теле процессы замедляются. Таким образом, длительность события, происходящего в некоторой точке, наименьшая в той инерциальной системе отсчета, относительно которой эта точка неподвижна. Следовательно, часы, движущиеся относительно инерциальной системы отсчета, идут медленнее покоящихся часов.

Скорость точки в системе I имеет составляющие (проекции на декартовы оси) а в системе II они . Это трехмерные векторы. В соответствии с преобразованиями Лоренца (16.4) составляем отношения:

     

     

     

     и окончательно получаем

     

		(16.6a)
	(16.6b)

     

(16.6c)

    

По этим формулам вычисляется скорость в системе II, если она известна в системе I. Аналогично находим обратные зависимости

     

(16.7a)

     

(16.7b)

     

(16.7c)

     

Частицы, двигающиеся со скоростями, сравнимыми со скоростью света, для которых необходимо использовать формулы (16.7), обычно называют, для краткости, релятивистскими частицами.

Таким образом, если материальная точка движется в системе II вдоль оси x′ со скоростью υ′ , а сама система II движется со скоростью u относительно системы I, то релятивистский закон сложения скоростей имеет вид:

    

Пример 1 . Относительно системы II свет распространяется в направлении оси х' со скоростью с. Подставляя значения в формулы (16.7), находим . Следовательно, скорость света относительно системы I равна тому же значению с, что согласуется со вторым постулатом Эйнштейна.