физика лекцыи_1 / 1.12 (2)

1.12. ГИДРОСТАТИКА И ГИДРОДИНАМИКА ИДЕАЛЬНОЙ НЕСЖИМАЕМОЙ ЖИДКОСТИ

Общие свойства жидкостей и газов. Понятие несжимаемой жидкости. Давление. Закон Паскаля. Идеальная и вязкая жидкость. Уравнения равновесия и движения жидкости. Гидростатика несжимаемой жидкости. Закон Архимеда. Кинематическое описание движения жидкости. Уравнение непрерывности струи. Закон Бернулли.

Жидкостью в гидравлике называют физическое тело способное изменять свою форму при воздействии на нее сколь угодно малых сил. Различают два вида жидкостей: жидкости капельные и жидкости газообразные (рис.12.1). Капельные жидкости представляют собой жидкости в обычном, общепринятом понимании этого слова (вода, нефть, керосин, масло и.т.д.). Газообразные жидкости - газы, в обычных условиях представляют собой газообразные вещества (воздух, кислород, азот, пропан и т.д.).

Рис. 12.1. Виды жидкостей

Основной отличительной особенностью капельных и газообразных жидкостей является способность сжиматься (изменять объем) под воздействием внешних сил. Капельные жидкости (в дальнейшем просто жидкости) трудно поддаются сжатию, а газообразные жидкости (газы) сжимаются довольно легко, т.е. при воздействии небольших усилий способны изменить свой объем в несколько раз.

Молекулы газа, совершая беспорядочное, хаотическое движение, не связаны или весьма слабо связаны силами взаимодействия, поэтому они движутся свободно и в результате соударений стремятся разлететься во все стороны, заполняя весь предоставленный им объем, т. е. объем газа, определяется объемом того сосуда, который газ занимает. Как и газ, жидкость принимает форму того сосуда, в который она заключена. Но в жидкостях в отличие от газов среднее расстояние между молекулами остается практически постоянным, поэтому жидкость обладает практически неизменным объемом.

Основным отличием жидкостей от твердых (упругих) тел является подвижность (текучесть). Благодаря своей подвижности жидкости, в отличие от упругих тел, не обнаруживают сопротивления изменению формы. Части жидкости могут свободно сдвигаться, скользя одна относительно другой. Поэтому, если к поверхности жидкости прилагаются силы, не перпендикулярные к поверхности, то равновесие жидкости всегда нарушается и она приходит в движение, как бы малы эти силы ни были.

Подвижностью жидкости объясняется то, что свободная поверхность жидкости, находящейся в равновесии под действием силы тяжести, всегда горизонтальна. В самом деле, если бы, например, поверхность покоящейся жидкости была расположена под углом к горизонту, то частицы жидкости вблизи поверхности соскальзывали бы вдоль нее вниз под действием силы тяжести, как по наклонной плоскости. Такое движение продолжалось бы, пока поверхность жидкости не сделалась бы горизонтальной.

В гидравлике рассматриваются реальная и идеальная жидкости. Идеальная жидкость в отличие от реальной жидкости не обладает внутренним трением, а также трением о стенки сосудов и трубопроводов, по которым она движется. Идеальная жидкость также обладает абсолютной несжимаемостью. Физическая модель несжимаемой жидкости – плотность которой всюду одинакова и не меняется со временем. Такая жидкость не существует в действительности, и была придумана для облегчения и упрощения ряда теоретических выводов и исследований.

Идеальной жидкостью называется воображаемая несжимаемая жидкость, в которой отсутствуют силы внутреннего трения. Вязкость — это свойство реальных жидкостей оказывать сопротивление перемещению одной части жидкости относительно другой.

Гидравлика делится на два раздела: гидростатика и гидродинамика. Гидростатикой называется раздел гидравлики, в котором рассматриваются законы равновесия жидкости и их практическое применение.

Повседневный опыт учит нас, что жидкости действуют с известными силами на поверхность твердых тел, соприкасающихся с ними. Эти силы мы называем силами давления жидкости.

Известно, что силы, действующие при непосредственном соприкосновении тел,— упругие силы — возникают в результате деформации тел. В твердых телах силы упругости возникают как при изменении формы, так и при изменении объема тела. В жидкостях при изменении формы силы упругости не возникают. Подвижность жидкости обусловлена именно отсутствием упругости по отношению к изменению формы. При изменении же объема (при сжатии жидкости) силы упругости возникают — по отношению к изменению объема жидкости обладают упругостью. Силы упругости в жидкости — это и есть силы давления. Таким образом, если жидкость действует с силами давления на соприкасающиеся с ней тела, то, значит, она сжата. Чем больше сжата жидкость, тем больше и возникающие в результате этого сжатия силы давления.

На каждый элемент поверхности ∆S тела, помещенного в жидкость, со стороны молекул жидкости действует сила ∆F направленная перпендикулярно поверхности. Давлением жидкости

(12.1)

называется физическая величина, определяемая нормальной силой, действующей со стороны жидкости на единицу площади.

Силы давления на стенки сосуда, заключающего жидкость, или на поверхность твердого тела, погруженного в жидкость, не приложены в какой-либо определенной точке поверхности. Они распределены по всей поверхности соприкосновения твердого тела с жидкостью. Поэтому сила давления на данную поверхность зависит не только от степени сжатия соприкасающейся с ней жидкости, но и от размеров этой поверхности.

Жидкость несжимаема, и ее плотность не зависит от давления. Тогда при поперечном сечении S столба жидкости, его высоте h и плотности ρ вес P = ρgSh, а давление на нижнее основание изменяется линейно с высотой давление ρgh называется гидростатическим.

(12.2)

В любой точке жидкости гидростатическое давление перпендикулярно площадке касательной к выделенному объему и действует внутрь рассматриваемого объема жидкости.

Закон Паскаля: Давление в любом месте покоящейся жидкости одинаково по всем направлениям, причем давление одинаково передается по всему объему, занятому покоящейся жидкостью.

Иногда формулируют закон Паскаля следующим образом: давление, создаваемое поверхностными силами, передается без изменения в каждую точку жидкости. В этой формулировке закон Паскаля остается верным и для общего случая, т. е. для случая, когда мы учитываем и силу тяжести. Если сила тяжести создает внутри покоящейся жидкости определенное давление (вообще говоря, различное в различных точках), то приложенные поверхностные силы увеличивают давление в каждой точке жидкости на одну и ту же величину.

Закон Паскаля позволяет объяснить действие распространенного в технике устройства — гидравлического пресса. Гидравлический пресс состоит из двух цилиндров разных диаметров, снабженных

Рис. 12.2. Схема гидравлического пресса

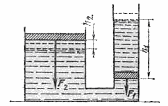Рис. 12.3. Перемещения поршней обратно пропорциональны их площадям, а значит, и силам, на них действующим

поршнями и соединенных трубкой (рис. 12.2). Пространство под поршнями и трубка заполняются жидкостью. Обозначим площадь малого поршня через S1, а большого поршня — через S2. Пусть к малому поршню приложена сила F1; найдем, какую силу F2 необходимо приложить ко второму поршню, чтобы сохранить равновесие, т. е. для того, чтобы жидкость не была вытеснена из первого цилиндра во второй или обратно через соединяющую их трубку.

Будем пренебрегать силой тяжести, действующей на жидкость; тогда давление во всех точках жидкости должно быть одним и тем же. Но давление под первым поршнем равно F1/S1 а под вторым — F2/S2; следовательно, F1/S1=F2/S2, откуда находим т. е. сила F2 во столько раз больше силы F1, во сколько раз площадь второго поршня больше площади первого. Таким образом, при помощи гидравлического пресса можно малой силой уравновесить большую силу.

Предположим теперь, что первый поршень переместился (например, опустился) на расстояние h1 (рис. 12.3); тогда часть жидкости поступает из первого цилиндра во второй и поднимет второй поршень на расстояние h2. Поскольку сжимаемость жидкостей незначительна, объем жидкости, вытесненный из первого цилиндра, можно считать равным объему, поступившему во второй, т. е. h1S1=h2S2.

Сравнивая эту формулу с формулой, полученной нами для силы F2, видим, что путь, проходимый большим поршнем, во столько раз меньше пути, проходимого меньшим поршнем, во сколько раз сила, действующая на большой поршень, больше силы, действующей на меньший.

Гидравлический пресс является преобразователем силы, подобно рассмотренным ранее простым машинам; его можно назвать гидравлической простой машиной. Для получения больших сил гидравлический пресс конструктивно удобнее рычажного или винтового пресса. Поэтому мощные прессы (например, для штамповки металла, для выжимания масла из семян растений и пр.) делаются гидравлическими. В качестве жидкости употребляются вода или масло.

Если тело, погруженное в жидкость, предоставить самому себе, то оно тонет, остается в равновесии или всплывает на поверхность жидкости в зависимости от того, меньше ли выталкивающая сила силы тяжести, действующей на тело, равна ей или больше ее. Выталкивающая сила зависит от рода жидкости, в которую погружено тело. Например, кусок железа тонет в воде, но плавает в ртути; значит, в воде выталкивающая сила, действующая на этот кусок меньше, а в ртути — больше силы тяжести.

Найдем выталкивающую силу, действующую на твердое тело, погруженное в жидкость. Выталкивающая сила, действующая на тело (рис. 12.4а), есть равнодействующая сил давления жидкости на его поверхность. Представим себе, что тело удалено и его место

занято той же жидкостью (рис. 12.4б).

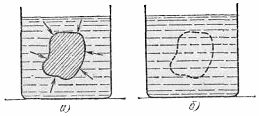Рис. 12.4. а) Тело находится в жидкости. б) Тело заменено жидкостью

Давление на поверхность такого мысленно выделенного объема будет таким же, каким было давление на поверхность самого тела. Значит, и равнодействующая сила давления на тело (выталкивающая сила) равна равнодействующей сил давления на выделенный объем жидкости. Но выделенный объем жидкости находится в равновесии. Силы, действующие на него,— это сила тяжести Р и выталкивающая сила F (рис. 12.5а). Значит, выталкивающая сила равна по модулю силе тяжести, действующей на выделенный объем жидкости, и направлена вверх. Точкой приложения этой силы должен быть центр тяжести выделенного объема. В противном случае равновесие нарушилось бы, так как сила

Рис. 12.5. а) Равнодействующая сил давления на поверхность погруженного тела равна силе тяжести, действующей на жидкость, объем которой равен объему тела, б) Если бы точка приложения равнодействующей силы не совпадала с центром тяжести вытесненного объема жидкости, то получилась бы пара сил и равновесие этого объема было бы невозможным тяжести и выталкивающая сила образовали бы пару сил (рис. 12.5. б). Но, как уже сказано, выталкивающая сила для выделенного объема совпадает с выталкивающей силой тела. Мы приходим, таким образом, к закону Архимеда:

Закон Архимеда: на тело, погруженное в жидкость или газ, действует со стороны этой жидкости (газа) направленная вверх выталкивающая сила, равная весу вытесненной телом жидкости (газа) - ρ — плотность жидкости, V — объем погруженного в жидкость тела.

(12.3)

Или выталкивающая сила, действующая на тело, погруженное в жидкость, равна по модулю силе тяжести, действующей на жидкость в объеме, занимаемом телом (вытесненный объем), направлена вертикально вверх и приложена в центре тяжести этого объема. Центр тяжести вытесненного объема называют центром давления.

Гидродинамика - раздел гидравлики, в котором изучаются законы движения жидкости и ее взаимодействие с неподвижными и подвижными поверхностями.

Движение жидкостей или газов представляет собой сложное явление. Для его описания используются различные упрощающие предположения (модели). В простейшей модели жидкость (или даже газ) предполагается несжимаемыми и идеальными (т. е. без внутреннего трения между движущимися слоями). При движении идеальной жидкости не происходит превращения механической энергии во внутреннюю, поэтому выполняется закон сохранения механической энергии. Следствием этого закона для стационарного потока идеальной и несжимаемой жидкости является уравнение Бернулли, сформулированное в 1738 г. Стационарным принято называть такой поток жидкости, в котором не образуются вихри. В стационарном потоке частицы жидкости перемещаются по неизменным во времени траекториям, которые называются линиями тока. Опыт показывает, что стационарные потоки возникают только при достаточно малых скоростях движения жидкости.

Рассмотрим стационарное движение идеальной несжимаемой жидкости по трубе переменного сечения (рис. 12.6). Различные части трубы могут находиться на разных высотах.

Рисунок 12.6. Течение идеальной жидкости по трубе переменного сечения. ΔV1 = l1S1; ΔV2 = l2S2. Условие несжимаемости: ΔV1 = ΔV2 = ΔV

За промежуток времени Δt жидкость в трубе сечением S₁ переместится на l₁ = υ₁Δt, а в трубе сечением S₂ – на l₂ = υ₂Δt, где υ₁ и υ₂ – скорости частиц жидкости в трубах. Условие несжимаемости записывается в виде:

ΔV = l1S1 = l2S2 или υ1S1 = υ1S1.

Здесь ΔV – объем жидкости, протекшей через сечения S₁ и S₂.

Таким образом, при переходе жидкости с участка трубы с большим сечением на участок с меньшим сечением скорость течения возрастает, т. е. жидкость движется с ускорением. Следовательно, на жидкость действует сила. В горизонтальной трубе эта сила может возникнуть только из-за разности давлений в широком и узком участках трубы. Давление в широком участке трубы должно быть больше чем в узком участке. Если участки трубы расположены на разной высоте, то ускорение жидкости вызывается совместным действием силы тяжести и силы давления. Сила давления – это упругая сила сжатия жидкости. Несжимаемость жидкости означает лишь то, что появление упругих сил происходит при пренебрежимо малом изменении объема любой части жидкости.

Так как жидкость предполагается идеальной, то она течет по трубе без трения. Поэтому к ее течению можно применить закон сохранения механической энергии.

При перемещении жидкости силы давления совершают работу:

ΔA = p1S1l1 – p2S2l2 = p1S1υ1Δt – p2S2υ2Δt = (p1 – p2)ΔV.

Работа ΔA сил давления равна изменению потенциальной энергии упругой деформации жидкости, взятому с обратным знаком.

Изменения, произошедшие за время Δt в выделенной части жидкости, заключенной между сечениями S₁ и S₂ в начальный момент времени, при стационарном течении сводятся к перемещению массы жидкости Δm = ρΔV (ρ – плотность жидкости) из одной части трубы сечением S₁ в другую часть сечением S₂ (заштрихованные объемы на рис. 12.6). Закон сохранения механической энергии для этой массы имеет вид:

E2 – E1 = ΔA = (p1 – p2)ΔV,

где E₁ и E₂ – полные механические энергии массы Δm в поле тяготения:

Отсюда следует:

Это и есть уравнение Бернулли. Из него следует, что сумма

остается неизменной вдоль всей трубы. В частности, для горизонтально расположенной трубы (h₁ = h₂) уравнение Бернулли принимает вид:

Величина p – статическое давление в жидкости. Оно может быть измерено с помощью манометра, перемещающегося вместе с жидкостью. Практически давление в разных сечениях трубы измеряется с помощью манометрических трубок, вставленных через боковые стенки в поток жидкости, так чтобы нижние концы трубок были параллельны скоростям частиц жидкости (рис. 12.7). Из уравнения Бернулли следует:

Давление в жидкости, текущей по горизонтальной трубе переменного сечения, больше в тех сечениях потока, в которых скорость ее движения меньше, и наоборот, давление меньше в тех сечениях, в которых скорость больше.

Рисунок 12.7. Измерение давления в потоке жидкости с помощью манометров. υ1 < υ2 < υ3; h1 > h2 > h3

Если сечение потока жидкости достаточно велико, то уравнение Бернулли следует применять к линиям тока, т. е. линиям, вдоль которых перемещаются частицы жидкости при стационарном течении. Например, при истечении идеальной несжимаемой жидкости из отверстия в боковой стенке или дне широкого сосуда линии тока начинаются вблизи свободной поверхности жидкости и проходят через отверстие (рис. 12.8).

Рисунок 12.8. Истечение жидкости из широкого сосуда

Поскольку скорость жидкости вблизи поверхности в широком сосуде пренебрежимо мала, то уравнение Бернулли принимает вид:

где p₀ – атмосферное давление, h – перепад высоты вдоль линии тока. Таким образом,

Это выражение для скорости истечения называют формулой Торричелли. Скорость истечения идеальной жидкости из отверстия в сосуде такая же, как и при свободном падении тела с высоты h без начальной скорости.

В отличие от жидкостей, газы могут сильно изменять свой объем. Расчеты показывают, что сжимаемостью газов можно пренебречь, если наибольшие скорости в потоке малы по сравнению со скоростью звука в этом газе. Таким образом, уравнение Бернулли можно применять к достаточно широкому классу задач аэродинамики.

10