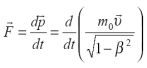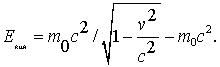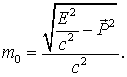1.17. ОСНОВЫ РЕЛЯТИВИСТСКОЙ ДИНАМИКИ

Релятивистский импульс. Уравнение движения частицы в специальной теории относительности. Работа и энергия. Полная энергия тела. Взаимосвязь энергии и массы, энергии и импульса.

Релятивистская динамика строится на основе постулатов Эйнштейна и их следствий - преобразований Лоренца, которые математически аккумулируют в себе метрические свойства пространства и времени.

Релятивистский импульс частицы

В релятивистской физике для описания механического движения вводятся 4-вектора положения частицы , перемещения и скорости . Вводим импульс по аналогии с ньютоновой механикой - как произведение инвариантной массы (массы покоя), одинаковой в инерциальных системах отсчета I и II, на 4-скорость. Итак, четырехмерным импульсом называется величина .

     

(17.1)

     Сокращенно пишем , где пространственная и временная компоненты 4-импульса имеют вид

     

.

(17.2)

     Здесь - так называемый релятивистский 3-импулъс. Очевидно, 4-импульсу отвечает его инвариант      

(17.3)

Масса покоя - - инвариант преобразований Лоренца. При небольших скоростях, когда , он переходит в инвариант преобразований Галилея.

Основное уравнение релятивистской динамики

В ньютоновой механике обычная трехмерная 3-сила определяется как скорость изменения во времени количества движения, переносимого на данное тело от окружающих тел и полей (равенство Ньютона является одновременно и определением силы, и законом движения). Аналогично в релятивистской механике будем определять силу как производную от релятивиского 3-импулься

(17.4)

Это равенство обобщает ньютонову трактовку 3-силы. В то же время оно представляет основной закон движения частицы (материальной точки) в инерциальной системе отсчета при любых возможных скоростях меньших с. Законы классической динамики получаются из законов релятивистской динамики в предельном случае υ << c.

Энергия свободной частицы. Связь между массой и энергией

В ньютоновой механике работа силы равна приращению кинетической энергии: . В СТО понятие силы обобщено, и работу релятивистской силы нужно заново вычислить. Найдем работу релятивистской силы на элементарном перемещении частицы

     

. (17.5)

 Здесь использовано правило дифференцирования произведения функций; учтено что и . Объединяя оба слагаемые под одним дифференциалом, окончательно получаем

     

(17.6)

Найденное равенство показывает, что работа силы равна приращению величины . Поэтому последнюю следует истолковать как энергию движущегося тела (частицы):

     

(17.7)

Эта формула, установленная Эйнштейном в 1905 г., в начале прошлого столетия вызывала сомнение, а позже обеспечила полный триумф теории относительности. Формула (17.7) устанавливает связь между массой (покоя) и энергией тела при его скорости .

Из формулы Эйнштейна вытекает важное открытие 20 века: любое тело в состоянии покоя обладает колоссальной энергией, которая называется энергией покоя и равна

   

.

(17.8)

Например, тело массой m₀ = l кг обладает энергией Дж, т.е. оно обладает энергией, которую, например, Днепровская ГЭС вырабатывает за 8 лет, давая в год 3 млрд. квт.-ч. энергии. Соотношение носит универсальный характер, оно применимо ко всем формам энергии, т.е.можно утверждать, что с энергией, какой бы формы она не была, связана масса и, наоборот, со всякой массой связана энергия.

Дадим определение: кинетической энергией тела называется разность

     

,

     откуда или

     

(17.9)

Формула (17.7) для энергии определяет сумму двух энергий: энергии покоя (она относится в внутренней энергии) и кинетической .

Связь между энергией и импульсом частицы

 Учитывая значения временной компоненты 4-импульса P₀ (формула (17.2)) и полной энергии Е (формула (17.7)), 4-импульс (формула (17.1)) можно представить в виде

     

(17.10)

     Как видим, в 4-импульсе объединились энергия Е и релятивистский 3-импульс , что означает глубокую внутреннюю связь между релятивистской энергией и релятивистским импульсом . При переходе из одной инерциальной системы отсчета в другую значение каждой из четырех компонент 4-импульса определяется по формулам Лоренца через все четыре компоненты в исходной системе I. Например, значение энергии в системе II определяется не только через энергию в системе I, но и через все компоненты импульса .

     Полезными являются также очевидные формулы для релятивистского импульса и его модуля в виде:

     

(17.11)

Релятивистские инварианты. Закон сохранения энергии-импульса

Определим величины, сохраняющиеся при переходе из одной системы отсчета в другую. Их обычно называются инвариантами. Как отмечалось, 4-импульсу соответствует инвариант

     

     Подставляя значение получаем

     

(17.12)

Это соотношение между релятивистской энергией и релятивистским импульсом выполняется как для частицы" так и для тела, и даже для сложной системы, так как при его выводе нигде не использовалась неделимость объекта. И общем случае в (17.12) под Е следует понимать полную энергию системы, а под - геометрическую сумму импульсов всех частей системы. Равенство (17.12) можно рассматривать так же как определение инвариантной массы (массы покоя) любой физической системы

     

(17.13)

В частном случае системы отсчета, в которой импульс равен нулю (), имеем

     

(17.14)

Следовательно, масса покоя тела определяет его энергию покоя (во всех ее видах). В релятивистской механике, в отличие от классической, энергия тела всегда положительна.

В другом частном случае, когда масса покоя равна нулю, соотношение (17.12) дает связь между релятивистским импульсом и энергией следующего вида

     

В частности, для для фотона с нулевой массой покоя эта формула преобразуется к виду

     

Вернемся к рассмотрению 4-импульса . Он объединяет релятивистскую энергию с релятивистским импульсом а значит представляет собой некоторую новую (одну единую!) величину, которую можно определить термином энергия-импульс. 4-вектору энергия-импульс соответствует инвариант (17.12), играющий важную роль в атомной и ядерной физике

     

     

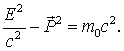
В случае изолированной физической системы эта величина сохраняется не только при переходе от системы отсчета I к системе II, но также сохраняется ее значение как до, так и после реакции, происходящей в физической системе.

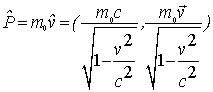
5