физика лекцыи_1 / 1.23

1.23. ВОЛНОВОЕ УРАВНЕНИЕ

Вывод волнового уравнения. Фазовая скорость в различных средах. Продольные волны в твердом теле. Плотность энергии среды в волновом поле. Перенос энергии волновым движением. Вектор Пойнтинга.

Волновое уравнение

Применяя второй закон Ньютона к упругой среде, можно получить дифференциальное уравнение в частных производных, решением которого будет уравнение волны. Логическая схема этого вывода такова:

Вывод закона Гука для бесконечно малого упругого стержня

Выделим элемент упругого стержня, длиной Δx.

Закрепим левую часть этого элемента (второй рисунок), правую сместим на величину Δξ вдоль оси x.

- закон Гука.

Здесь коэффициент k_упр, характеризующий упругость стержня, зависит от материала стержня, его длины и площади сечения.

Нормальное напряжение и относительная деформация

Введем:

- нормальное напряжение, (23.1)

- относительная деформация. (23.2а)

При Δx → 0

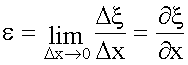. (23.2б)

Перепишем , выразив F и Δξ через σ и ε :

или

.

Модуль Юнга

Величина не зависит от длины и сечения стержня, она определяется только упругими свойствами материала, ее называют модулем Юнга материала:

.

Закон Гука

Тогда связь нормального напряжения σ и относительной деформации ε будет иметь вид:

. (23.3)

Это выражение тоже носит название закона Гука.

Вывод волнового уравнения из .

Пусть волна распространяется вдоль упругого стержня. Рассмотрим элемент этого стержня, его длина равна Δx в невозмущенном состоянии. Пусть при распространения волны левая часть этого элемента сместится на величину ξ(x), а правая - на величину ξ(x + Δx), не равную смещению левой части.

В нашем примере стержень растянут внешними силами:

Сумма этих сил равна:

.

Домножим и поделим последнее выражение на Δ x. Величина

при Δx → 0 дает вторую производную от "кси" по x, т.е. .

Тогда .

Масса нашего элемента , его ускорение

,

тогда преобразуется в

,

или

- волновое уравнение. (23.4)

Проверим, будет ли его решением.

Откуда

.

Т.к. , то фазовая скорость упругой продольной волны:

(23.5)

и волновое уравнение можно записать в виде:

. (23.6)

Для волны, распространяющейся в произвольном направлении, волновое уравнение имеет вид:

. (23.7)

Найдем полную механическую энергию для выделенного нами элемента упругой среды, в которой распространяются упругая продольная волна:

Скорость:

,

тогда

. (23.8)

Потенциальная энергия упругого деформированного стержня:

. (23.9)

Полная энергия выделенного элемента объемом SΔx будет равна:

. (23.10)

Плотность энергии упругой волны

. (23.11)

Плотность энергии упругой гармонической волны

(23.12)

Среднее по времени значение плотности энергии упругой гармонической волны

, это известно из математики, значит:

. (23.13)

Поток энергии - среднее количество энергии, переносимое волной за единицу времени через поперечное сечение S

(23.14)

Плотность потока энергии. Количество энергии, переносимое волной за единицу времени через единицу площади поверхности, расположенной перпендикулярно направлению распространения волны, называется плотностью потока энергии волны.

(23.15)

Вектор Умова-Пойнтинга - связь плотности потока энергии с плотностью энергии упругой волны

Так как фазовая скорость волны v - вектор, направление которого совпадает с направлением распространения волны, то можно величине плотности потока энергии j придать смысл векторной величины:

j = wv. (23.16)

Величина j, вектор плотности энергии волны, впервые была введена Н.А. Умовым в 1984 году и получила название вектора Умова. Подобная величина для электромагнитных волн называется вектором Умова - Пойнтинга.

Интенсивность волны

- это среднее по времени от модуля вектора плотности потока энергии:

.

Для гармонической волны:

. (23.17)

Фазовая скорость различна для разных сред.

В случае упругих поперечных волн (в твердом теле) фазовая скорость равна:

,

где - модуль сдвига среды, -ее плотность в невозбужденном состоянии (т.е. когда в этой среде не распространяется упругая волна).

Фазовая скорость упругих продольных волн в твердом теле равна

,

где Е - модуль Юнга, - плотность невозмущенной среды (твердого тела до момента распространения по нему волны).

Фазовая скорость продольных волн в жидкости и газе определяется соотношением:

,

где К – модуль объемной упругости среды – величина, характеризующая способность среды сопротивляться изменению ее объема, - плотность невозмущенной среды.

Фазовая скорость продольных волн в идеальном газе задается формулой:

,

- показатель адиабаты, - молярная масса, Т – абсолютная температура, R – универсальная газовая постоянная. Фазовая скорость в газе зависит от сорта газа () и от его термодинамического состояния (Т).

7