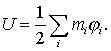физика лекцыи_1 / 1

1.7. ЗАКОН СОХРАНЕНИЯ МЕХАНИЧЕСКОЙ ЭНЕРГИИ

Формулировка закона сохранения механической энергии. Формулировка в случае наличия диссипативных сил. Графическое представление энергии. Финитное и инфинитное движения. Абсолютно упругий удар. Абсолютно неупругий удар.

Полная механическая энергия системы — энергия механического движения и взаимодействия, т.е. равна сумме кинетической и потенциальной энергий. Закон сохранения механической энергии: в системе тел, между которыми действуют только консервативные силы полная механическая энергия сохраняется, т.е. не изменяется со временем. Это —фундаментальный закон природы. Он является следствием однородности времени — инвариантности физических законов относительно выбора начала отсчета времени. Все силы в механике принято разделять на консервативные и неконсервативные. Консервативными называются силы, работа которых не зависит от формы траектории (пути) между двумя точками, а зависит только от начального и конечного положений тела относительно другого. Иначе говоря, работа консервативных сил по замкнутой траектории равна нулю. Примером консервативных сил являются сила тяжести, сила упругости и т.д. К ним, прежде всего, относятся диссипативные силы (преобразующие механическую энергию в другие виды энергии), например, сила трения. Если есть изменение, то равна работе диссипативных сил. Финитное – движение точек в ограниченной области пространства. Инфинитное – тело уходит на бесконечность. Абсолютно упругий удар — столкновение двух тел, в результате которого в обоих взаимодействующих телах не остается никаких деформаций и вся кинетическая энергия, которой обладали тела до удара, после удара снова превращается в кинетическую энергию. законы сохранения импульса и сохранения механической энергии выполняются. Абсолютно неупругий удар — столкновение двух тел, в результате которого тела объединяются, двигаясь дальше как единое тело. Не выполняется закон сохранения механической энергии: вследствие деформации часть кинетической энергии переходит во внутреннюю энергию тел (разогрев).

Введем понятие полной механической энергии частицы. Приращение кинетической энергии частицы равно элементарной работе результирующей всех сил, действующих на частицу. Если частица находится в потенциальном поле, то на нее действует консервативная сила со стороны этого потенциального поля. Кроме того, на частицу могут действовать и другие силы, имеющие иное происхождение. Назовем их сторонними силами .

Таким образом, результирующая всех сил, действующих на частицу, может быть представлена в виде . Работа всех этих сил идет на приращение кинетической энергии частицы:

     

 Согласно (6.7), работа сил поля равна убыли потенциальной энергии частицы, т. е. . Подставив это выражение в предыдущее и перенеся член влево, получим

     

Отсюда видно, что работа сторонних сил идет на приращениe величины . Эту величину - сумму кинетичеcкой и потенциальной энергии - называют полной механической энергией частицы в поле:

     

(7.1)

Заметим, что полная механическая энергия Е, как и потенциальная, определяется с точностью до прибавления несущественной произвольной постоянной.

     

Итак, приращение полной механической энергии частицы на элементарном перемещении равно

     

(7.2)

на конечном перемещении из точки 1 в точку 2

     

(7.3)

т.е. приращение полной механической энергии частицы на некотором пути равно алгебраической сумме работ всех сторонних сил, действующих на частицу на том же пути. Если , то полная механическая энергия частицы увеличивается, если же , то уменьшается.

Полная механическая энергия частицы может измениться под действием только сторонних сил. Отсюда непосредственно вытекает закон сохранения полной механической энергии частицы во внешнем поле: если сторонние силы отсутствуют или таковы, что алгебраическая сумма их мощностей равна нулю в течение интересующего нас времени, то полная механическая энергия частицы остается постоянной за это время. Иначе говоря,

     

     или

     

(7.4)

Уже в такой простейшей форме данный закон сохранения позволяет достаточно легко получать ответы на ряд важных вопросов без привлечения уравнений движения, что, как мы знаем, часто сопряжено с проведением громоздких и утомительных расчетов. Именно это обстоятельство и превращает законы сохранения в весьма действенный инструмент исследования.

     

Проиллюстрируем возможности и преимущества, которые дает применение закона сохранения (7.4), на следующем примере.

     

Пример. Пусть частица движется в одномерном потенциальном поле U(х. Если сторонние силы отсутствуют, то полная механическая энергия частицы в данном поле, т. е. Е, не меняется в процессе движения, и мы можем просто решить, например, такие вопросы, как:

     1. Определить, не решая основного уравнения динамики, v(х) - скорость частицы в зависимости от ее координаты. Для этого достаточно знать, согласно уравнению (7.4), конкретный вид потенциальной кривой U(х) и значение полной энергии Е (правая часть данного уравнения).

     2. Установить область изменения координаты х частицы, в которой она может находиться при заданном значении полной энергии Е. Ясно, что в область, где U > Е, частица попасть не может, поскольку потенциальная энергия U частицы не может превышать ее полную энергию. Отсюда сразу следует, что при (рис. 7.1) частица может двигаться в области

Рис. 7.1. Области возможного движения частицы в потенциальном поле

 между координатами (совершает колебания) или правее координаты . Перейти же из первой области во вторую (или обратно) частица не может: этому препятствует потенциальный барьер, разделяющий обе эти области. Заметим, что когда частица движется в ограниченной области поля, говорят, что она находится в потенциальной яме, в нашем случае - между .

Иначе ведет себя частица при (рис. 7.1): для нее доступна вся область правее . Если в начальный момент частица находилась в точке, то в дальнейшем она будет двигаться вправо. Определение изменения кинетической энергия частицы в зависимости от ее положения х может послужить полезным самостоятельным упражнением.

     

До сих пор мы ограничивались рассмотрением поведения одной частицы с энергетической точки зрения. Теперь перейдем к системе частиц. Это может быть любое тело, газ, любой механизм, Солнечная система и т. д.

    

В общем случае частицы системы могут взаимодействовать как между собой, так и с телами, не входящими в данную систему. Систему частиц, на которую не действуют никакие посторонние тела или их воздействие пренебрежимо мало, называют замкнутой или изолированной. Понятие замкнутой системы является естественным обобщением понятия изолированной материальной точки и играет важную роль в физике.

     

Введем понятие потенциальной энергии системы частиц. Рассмотрим замкнутую систему, между частицами которой действуют только центральные силы, т. е. силы, зависящие при данном характере взаимодействия только от расстояния между ними и направленные по прямой, их соединяющей.

     

Покажем, что в любой системе отсчета работа всех этих сил при переходе системы частиц из одного положения в другое может быть представлена как убыль некоторой функции, зависящей при данном характере взаимодействия только от конфигурации самой системы или от относительного расположения ее частиц. Эту функцию назовем собственной потенциальной энергией системы, в отличие от внешней потенциальной энергии, характеризующей взаимодействие данной системы с другими телами.

     Первоначально рассмотрим систему из двух частиц. Вычислим элементарную работу сил, с которыми эти частицы взаимодействуют между собой. Пусть в произвольной системе отсчета в некоторый момент времени положение частиц определяется радиус-векторами и . Если за время dt частицы совершили перемещения и соответственно, то работа сил взаимодействия и равна

     

Теперь учтем, что, согласно третьему закону Ньютона , поэтому предыдущее выражение можно переписать так:

     

Введем вектор , характеризующий положение 1-й частицы относительно 2-й. Тогда и после подстановки в выражение для работы получим

     

.

Сила - центральная, поэтому работа этой силы равна убыли потенциальной энергии взаимодействия данной пары частиц, т. е.

     

Так как функция зависит только от расстояния между частицами, то ясно, что работа не зависит от выбора системы отсчета.

     

Теперь рассмотрим систему из трех частиц, так как полученный в этом случае результат легко обобщить и на систему из произвольного числа частиц. Элементарная работа, которую совершают все силы взаимодействия при элементарном перемещении всех частиц, может быть представлена как сумма элементарных работ всех трех пар взаимодействий, т. е.

     

 Но для каждой пары взаимодействий, как было показано , поэтому

     

 где функция есть собственная потенциальная энергия данной системы частиц:

     

Так как каждое слагаемое этой суммы зависит от расстояния между соответствующими частицами, то очевидно, что собственная потенциальная энергия U данной системы зависит от относительного расположения частиц в один и тот же момент времени, или, другими словами, от конфигурации системы.

     

Подобные рассуждения справедливы и для системы из любого числа частиц. Поэтому можно утверждать, что каждой конфигурации произвольной системы частиц присуща своя собственная потенциальная энергия U, и работа всех центральных внутренних сил при изменении конфигурации системы равна убыли собственной потенциальной энергии системы, т. е.

     

(7.5)

 а при конечном перемещении всех частиц системы

     

(7.6)

где и -значения потенциальной энергии системы в начальном и конечном состояниях.

     

Собственная потенциальная энергия системы U - величина неаддитивная, т. е. она не равна в общем случае сумме собственных потенциальных энергий ее частей. Необходимо учесть еще потенциальную энергию взаимодействия отдельных частей системы

     

,

(7.7)

     где - собственная потенциальная энергия части системы.

     

Следует также иметь в виду, что собственная потенциальная энергия системы, как и потенциальная энергия взаимодействия каждой пары частиц, определяется с точностью до прибавления произвольной постоянной, которая, впрочем, и здесь совершенно несущественна.

     

В заключение приведем полезные формулы для расчета собственной потенциальной энергии системы. Прежде всего покажем, что эта энергия может быть представлена как.

     

(7.8)

где - потенциальная энергия взаимодействия частицы со всеми остальными частицами системы. Здесь сумма берется по всем частицам системы. Убедимся в справедливости этой формулы сначала для системы из трех частиц. Выше было показано, что собственная потенциальная энергия данной системы Преобразуем эту сумму следующим образом. Представим каждое слагаемое в симметричном виде: , ибо ясно, что . Тогда

     

     Сгруппируем члены с одинаковым первым индексом:

     

     Каждая сумма в круглых скобках представляет собой потенциальную энергию взаимодействия частицы с остальными двумя. Поэтому последнее выражение можно переписать так:

     

     что полностью соответствует формуле (7.8).

     

Обобщение полученного результата на произвольную систему очевидно, ибо ясно, что подобные рассуждения совершенно не зависят от числа частиц, составляющих систему.

     

Для системы, взаимодействие между частицами которой носит гравитационный или кулоновский характер, формулу (7.8) можно преобразовать и к другому виду, воспользовавшись понятием потенциала. Заменим в (7.8) потенциальную энергию частицы выражением , где - масса (заряд) частицы, а - потенциал, создаваемый всеми остальными частицами системы в точке нахождения частицы.

     Тогда

     

(7.9)

Если массы или заряды распределены в системе непрерывно, то суммирование сводится к интегрированию:

     

(7.10)

где -объемная плотность массы или заряда, -элемент объема. Здесь интегрирование проводится по всему объему, занимаемому массами или зарядами.

Проведем классификацию сил по их свойствам. Известно, что частицы рассматриваемой системы могут взаимодействовать как между собой, так и с телами, не входящими в данную систему. В соответствии с этим силы взаимодействия между частицами системы называют внутренними, а силы, обусловленные действием других тел, не входящих в данную систему, - внешними. В неинерциальной системе отсчета к последним нужно относить и силы инерции.

     

Кроме того, все силы делят на потенциальные и непотенциальные. Потенциальными называют силы, зависящие при данном характере взаимодействия только от конфигурации механической системы. Работа этих сил, как было показано, равна убыли потенциальной энергии системы. К непотенциальным силам относятся так называемые диссипативные силы - это силы трения и сопротивления, а также энергетические силы, вызывающие увеличение механической энергии системы за счет других видов энергии (например, взрыв артиллерийского снаряда). Важной особенностью данных сил является то, что суммарная работа внутренних диссипативных сил рассматриваемой системы отрицательна, а энергетических сил - положительна, причем в любой системе отсчета. Докажем это для диссипативных сил.

Любая диссипативная сила может быть представлена в виде

     

(7.14)

где - скорость данного тела относительно другого тела (или среды), с которым оно взаимодействует; - положительный коэффициент, зависящий в общем случае от скорости . Сила всегда направлена противоположно вектору . В зависимости от выбора системы отсчета работа этой силы может быть как положительной, так и отрицательной. Суммарная же работа всех внутренних диссипативных сил - величина всегда отрицательная. Переходя к доказательству этого, отметим прежде всего, что внутренние диссипативные силы в данной системе будут встречаться попарно, причем в каждой паре, согласно третьему закону Ньютона, они одинаковы по модулю и противоположны по направлению. Найдем элементарную работу произвольной пары диссипативных сил взаимодействия между телами 1 и 2 в системе отсчета, где скорости этих тел в данный момент равны :

     

Теперь учтем, что - скорость тела 1 относительно тела 2, а также то, что . Тогда выражение для работы преобразуется так:

     

,

Отсюда видно, что работа произвольной пары внутренних диссипативных сил взаимодействия всегда отрицательна, а значит и суммарная работа всех пар внутренних диссипативных сил также всегда отрицательна. Таким образом, действительно,

     

(7.15)

     

Теперь можно сформулировать закон сохранения полной механической энергии системы частиц. Выше было показано, что приращение кинетической энергии системы равно работе, которую совершают все силы, действующие на все частицы системы. Разделив эти силы на внешние и внутренние, а внутренние, в свою очередь,- на потенциальные и непотенциальные, запишем предыдущее утверждение так:

     

Теперь учтем, что работа внутренних потенциальных сил равна убыли собственной потенциальной энергии системы, т.е.

     

Тогда предыдущее выражение примет вид

     

(7.16)

Введем понятие полной механической энергии системы, или, короче, механической энергии, как сумму кинетической и потенциальной энергии системы:

     

(7.17)

     

Очевидно, энергия Е зависит от скоростей частицы системы, характера взаимодействия между ними и конфигурации системы. Кроме того, энергия Е, как и потенциальная энергия U, определяется с точностью до прибавления несущественной произвольной постоянной и является величиной неаддитивной, т. е. энергия Е системы не равна в общем случае сумме энергий ее отдельных частей. В соответствии c (7.7)

     

(7.18)

где - механическая энергия части системы, - потенциальная энергия взаимодействия ее отдельных частей.