физика лекцыи_1 / 1.14

Механические свойства твердых тел.

По характеру изменения формы тела можно выделить деформации растяжения и сжатия, кручения, изгиба, сдвига.

Виды упругих деформаций:

1. Линейная:

а) Растяжение (тросы подъемных кранов, канатных дорог, буксирные тросы)

б) Сжатие (колонны, стены, фундаменты зданий).

При растяжении тела удлиняются и одновременно уменьшаются в поперечных размерах. Это хорошо видно при растяжении плоского резинового жгута, на котором начерчена сетка линий.

Растяжение

2. Сдвиг (заклепки, болты, соед. металлические конструкции, процесс разрезания ножницами бумаги).

Деформация сдвига обусловливается двумя равными по модулю и противоположными по направлению моментами сил. При сдвиге любой мысленно выделенный в теле прямоугольный параллелепипед превращается в наклонный, равный ему по объему.

Сдвиг возникает во всех трущихся телах как при трении покоя, так и при трении скольжения. Деформации сдвига подвергаются заклепки, скрепляющие два листа, если эти листы растягиваются. Сдвигаются и волокна бумаги при разрезании ее ножницами.

Сдвиг

3. Кручение (завинчивание гаек, работа валов машин, сверление металлов и т.п.).

Чтобы пронаблюдать деформацию кручения, можно взять в руки резиновый стержень, вдоль образующей которого проведена прямая линия, и повернуть его в разных направлениях. Линия примет винтовую форму.

Деформации кручения подвергаются валы, передающие вращающий момент от двигателей к колесам автомобилей и гребным винтам теплоходов. Эту же деформацию испытывает ручка отвертки при заворачивании шурупа. Растягивание цилиндрической пружины также приводит к кручению проволоки, из которой она изготовлена.

4. Изгиб (формально деформация растяжения и сжатия, различная в разных частях тела. Нейтральный слой - слой, не подвергающийся ни растяжению, ни сжатию, при изгибе.)

Деформацию изгиба можно пронаблюдать, закрепив на столе линейку и подвесив к ее концу груз.

Изгиб испытывают потолочные плиты зданий, железнодорожные рельсы, рычаги.

Деформацию растяжения и сжатия можно охарактеризовать абсолютной деформацией Dℓ, равной разности длин образца после растяжения ℓ и до него ℓ₀: Dℓ = ℓ – ℓ₀

Dℓ = ℓ – ℓ₀

Отношение абсолютной деформации Dℓ к первоначальной длине образца ℓ_o называют относительной деформацией:

Силы упругости. При деформациях твердого тела его частицы (атомы, молекулы, ионы), находящиеся в узлах кристаллической решетки, смещаются из своих положений равновесия. Этому смещению противодействуют силы взаимодействия между частицами твердого тела, удерживающие эти частицы на определенном расстоянии друг от друга. Поэтому при любом виде упругой деформации в теле возникают внутренние силы, препятствующие его деформации.

Силы, возникающие в теле при его упругой деформации и направленные против направления смещения частиц тела, вызываемого деформацией, называют силами упругости. Силы упругости действуют в любом сечении деформированного тела, а также в месте его контакта с телом, вызывающим деформации. В случае одностороннего растяжения или сжатия сила упругости направлена вдоль прямой, по которой действует внешняя сила, вызывающая деформацию тела, противоположно направлению этой силы и перпендикулярно поверхности тела

Если деформация упругая, то справедлив закон Гука: . Сила упругости при малых упругих деформациях прямо пропорциональна абсолютной деформации.

С учетом направления:

k - коэффициент жесткости (упругости). Зависит от материала, формы и размеров тела (Например, чем длиннее и тоньше пружина, тем ее жесткость меньше.)

Единицы коэффициента упругости в СИ: .

Движение под действием силы упругости.

- ускорение изменяется с координатой! Это неравнопеременное движение. Такое движение является колебательным.

Частные случаи силы упругости:

1. Сила реакции опоры - направлена всегда перпендикулярно поверхности.

2. Сила натяжения (нити, сцепки)

Физическая величина, равная отношению модуля силы упругости F_упр, возникающей при деформации, к площади сечения S образца, перпендикулярного вектору силы F. называется механическим напряжением: . За единицу механического напряжения в СИ принята единица паскаль (Па): 1 Па= 1Н/м².

Отношение механического напряжения к относительному удлинению , при малых упругих деформациях растяжения и сжатия, называется модулем упругости Е (модулем Юнга): .

Из выше написанной формулы видно, что модуль Юнга Е величина не зависящая от формы и размеров предмета, изготовленных из данного материала. [Е]=Па. Модуль Юнга показывает, какое надо создать механическое напряжение, чтобы деформировать тело в 2 раза (Если - на самом деле нереально).

[Е]=Па

Если обозначить ,

то получим F_упр =k|Dl| - закон Гука. Другая форма записи этого закона: s = E|e| - механическое напряжение прямо пропорционально модулю относительной деформации.

s = E|e|

Энергия упруго деформированного тела. При растяжении или сжатии стержня внешние силы совершают работу. Из закона Гука следует, что сила не остается во время деформации постоянной. Она меняется пропорционально изменению длины стержня ΔL.

Вычислим работу такой переменной силы. Пусть длина стержня меняется от значения L до L + ΔL, тогда работа А равна:

где представляет собой среднее значение силы. Ввиду линейности возрастания силы F с удлинением ΔL, среднее значение силы равно среднему арифметическому из значений силы F = 0 (при ΔL = 0) и (при данном ΔL), то есть

откуда

Таким образом, потенциальная энергия упруго деформированного стержня оказывается пропорциональной квадрату абсолютного удлинения образца.

В материаловедении модулем сдвига (обозначается буквой G или μ), называется отношение касательного напряжения к сдвиговой деформации

Здесь

 — касательное напряжение;

 — действующая сила;

 — площадь, на которую действует сила;

 — сдвиговая деформация;

 — смещение;

 — начальная длина.

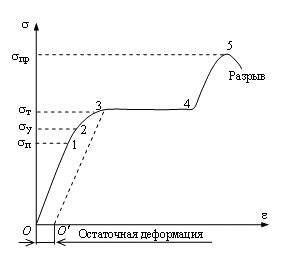
Диаграмма растяжения-сжатия. Диаграммой растяжения принято называть графическую зависимость σ от ε.

На участке 0–1 график имеет вид прямой, проходящей через начало координат. Это значит, что до определенного значения напряжения деформация является упругой и выполняется закон Гука, согласно которому нормальное напряжение пропорционально относительному удлинению. Максимальное значение нормального напряжения σ_П, при котором еще выполняется закон Гука, называют пределом пропорциональности.

При дальнейшем увеличении нагрузки зависимость напряжения от относительного удлинения становится нелинейной (участок 1–2), хотя упругие свойства тела еще сохраняются. Максимальное значение σ_y нормального напряжения, при котором еще не возникает остаточная деформация, называют пределом упругости. (Предел упругости лишь на сотые доли процента превышает предел пропорциональности). Увеличение нагрузки выше предела упругости (участок 2–3) приводит к тому, что деформация становится остаточной.

Затем образец начинает удлиняться практически при постоянном напряжении (участок 3–4 графика). Это явление называют текучестью материала. Нормальное напряжение σ_Т, при котором остаточная деформация достигает заданного значения, называют пределом текучести.

При напряжениях, превышающих предел текучести, упругие свойства тела в известной мере восстанавливаются, и оно вновь начинает сопротивляться деформации (участок 4–5 графика).

Максимальное значение нормального напряжения σ_пр, при превышении которого происходит разрыв образца, называют пределом прочности.

s_п - предел пропорциональности (максимальное напряжение, при котором деформация еще остается упругой и выполняется закон Гука)

s_уп - предел упругости (максимальное напряжение, при котором еще не возникают заметные остаточные деформации, и материал еще сохраняет упругие свойства)

s_т - предел текучести (напряжение, при котором материал "течет")

s_пч - предел прочности (наибольшее напряжение, которое способен выдержать образец без разрушения)

e_ост- остаточная деформация

Коэффициент безопасности (предел прочности) - отношение предела пропорциональности данного материала к максимальному напряжению, которое будет испытывать деталь конструкции в работе: .

В зависимости от необходимой надежности различных деталей и конструкций коэффициент безопасности выбирают обычно в пределах от 2 до 10.