
Sebery J.Cryptography.An introduction to computer security.1989
.pdf3.4 Di erential Cryptanalysis |
121 |
3.4.1 XOR Pro les
The basic tool used in the analysis is a table which shows di erences between input and output of S-boxes. This table is further referred to as the XOR pro le of an S-box. Assume that we have an S-box that transforms input strings according to the following function
f : n ! m:
For a given pair of input strings (s1; s2), the S-box generates outputs s1
f(s1) and s2 = f(s2). The pair of input/output tuples f(s1; s1);(s2; s2)g characterized by their input and output XOR di erences Æ = s1 s2 and
s1 s2. Denote
SÆ = f(s1; s2; s1; s2) j s1 s2 = Æ; s1 s2 = ;
s1; s2 2 n; s1; s2 2 m; s1 = f(s1); s2 = f(s2)g
=
is
=
the set consists of elements (four-tuples) whose Æ and are xed. For in-
stance, the set 3Cx = (3x; 3Fx; Fx; Dx), (17x; 2Bx; Bx; 9x), (2Bx; 17x; 9x; Bx),
S2x f
(3Fx; 3x; Dx; Fx)g is computed for S1 of DES. It means that there are four elements in the set. Note that there are actually two di erent elements only as the remaining two are permutations of their inputs and outputs. That is why
the cardinality of SÆ is always an even number. There are also some Æ and
for which the set SÆ is empty. Indeed, any set S0x for 6= 0 is empty. This
happens because any 4-tuple for two identical inputs is of the form (xi; xi; yi; yi)
and the corresponding must be zero. The number of 4-tuples in S00xx is equal to 2n.
De nition 2. The XOR pro le of an S-box de ned by f : n ! m is a table which has 2n rows and 2m columns. Each row and column is indexed by Æ and, respectively. Each entry (Æ, ) of the table shows the number of elements in the set SÆ .
The XOR pro le of the DES S1 is presented in Table 3.13. For the full collection of XOR pro les of other DES S-boxes, the reader is referred to [35]. For the rest of this section we will use S1 of DES in our examples.
The properties of XOR pro les can be summarized as follows: { All entries in the table are zeroes or positive even integers.
122 3 PRIVATE-KEY CRYPTOSYSTEMS
s1 |
s 2 |
k |
k |
s1 + k |
s2 + k |
S1 |
S1 |
s* |
s* |
1 |
2 |
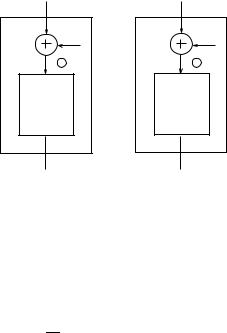
Fig. 3.25. Di erential analysis of S1
{The row for Æ = 0 has only one nonzero entry equal to 2n (n is the number of input bits of the S-box).
{The sum of entries in each row is equal to 2n.
{An input di erence Æ may cause an output di erence with probability
p = |
|
where is the entry of (Æ; ). In other words, is the number of |
2n |
input pairs (s1; s1 Æ) such that the corresponding output di erence is , where s1 2 n, This is denoted as Æ ! .
{ If an entry (Æ; ) is zero, then the input di erence Æ cannot cause the di erence on the output.
Suppose both Æ and are known. What can be said about actual val-
ues of the input? Obviously, the input must occur in some tuples from SÆ . |
||||
|
3Cx |
computed for S1 of |
|
|
For example, |
the set S2x |
DES contains four |
inputs |
|
s 2 f3x; 3Fx; 17x;2Bxg. Consider the DES S1 with a 6-bit partial key k XORed |
||||
to the input |
(Figure 3.25). The XOR pro le of |
S1 with the key is |
identi- |
|
cal to the XOR pro le of the original S-box. This results from the fact that (s1 k) (s2 k) = s1 s2. The di erential attack is based on this observation and exploits the fact that the XOR pro le does not depend on the cryptographic key used.
Now assume that the values s1, s2 and are known. What we can say about the key? First, observe that both s1 k and s2 k must occur in SÆ where Æ = s1 s2. So we can extract all input values from the set SÆ . Let the set of
the inputs be X = fsi1 ; : : : ; sij g where j =j SÆ j. Then the key k must belong to the set K = X s1= X s2= fsi1 s1; : : : ; sij s1g = fsi1 s2; : : : ; sij s2g.
3.4 Di erential Cryptanalysis |
123 |
Consider an example. Let an input (s1; s2) = (21x;38x) have the output di erence = 1x. The set
19x = (2x; 1Bx; 4x; 5x); (1Bx; 2x; 5x; 4x);
S1x f
(22x; 3Bx; 1x; 0x); (2Cx; 35x; 2x; 3x); (35x; 2Cx; 3x; 2x); (3Bx; 22x; 0x; 1x)g:
The collection of all inputs is X = f2x; 1Bx;22x;3Bx; 2Cx; 35xg. The applied key must be in the set K1 = X s1 = X s2 = f23x; 3Ax; 3x; 1Ax; Dx; 14xg. If the second observation is done for the input (s1; s2) = (14; 23) and = 2x. The set S237xx has 12 elements and is equal to
37x = (Ex; 39x; 8x; Ax); (Fx; 38x; 1x; 3x);
S2x f
(11x; 26x; Ax; 8x); (12x; 25x; Ax; 8x); (18x; 2Fx; 5x; 7x); (19x; 2Ex; 9x; Bx); (25x; 12x; 8x; Ax); (26x; 11x; 8x; Ax); (2Ex; 19x; Bx; 9x); (2Fx; 18x; 7x; 5x); (38x; Fx; 3x; 1x); (39x; Ex; Ax; 8x)g:
The set of inputs is X = fEx; 39x; Fx; 38x; 11x; 26x; 12x; 25x; 18x; 2Fx; 19x; 2Exg. The key applied must be in the set K2 = X s1 = X s2 = f1Ax; 2Dx; 2Cx;
1Bx; 32x; 5x; 31x; 6x; 3Bx; Cx; 3Ax; Dxg. The intersection of the sets K1 \K2 = f1Ax; Dx; 3Axg. The secret key must be there. Yet another observation should
be enough to nd out the unique key. Indeed, let (s1; s2) = (14x; 1Cx) and = 9x, then we have X = f6x; Ex; 20x; 28x; 25x; 2Dxg and K3 = X s1 = X s2 = f12x; 1Ax; 34x; 3Cx; 31x; 39x; g. The only key in all sets K1; K2; K3 is 1Ax.
At this stage we know how a single S-box can be analyzed using input observations and the corresponding output di erences. The following points summarize our considerations:
{The XOR pro le of an S-box with the secret key XORed with the input is identical to the XOR pro le of the S-box without the key.
{Every input observation (s1; s2) and the corresponding output di erence enables the cryptanalyst to nd out a set K of key candidates and
Æ
j K j=j S j
s2 and = f (s1) f(s2).
{The analysis of di erences for a single S-box allows one to retrieve the key that is XORed to the input of an S-box.
124 3 PRIVATE-KEY CRYPTOSYSTEMS
Ω in = (δ A , 0 )
∆ 1 = 0 |
δ |
1 = 0 |
|
f |
|
Ωout = ( δ A , 0 )
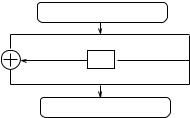
Fig. 3.26. A single round characteristic of DES
Now we would like to extend our analysis to the DES algorithm. Consider the last round of DES. As DES uses Feistel permutations, inputs to all S-boxes used in the last round can be observed by looking at the second half of the cryptogram. The problem is that we cannot see the corresponding output di erences. Fortunately, Biham and Shamir demonstrated that there is a probabilistic argument that allows one to make guesses about . To explain the idea, we need to introduce the so-called characteristics of DES rounds.
3.4.2 DES Round Characteristics
An important feature of XOR pro les is that the input di erence Æ = 0 forces the output di erence to be zero as well. Consider a single DES round with two input sequences (A1; 0) and (A2; 0). So their input di erence is in = (A1 A2; 0) = (ÆA; 0). The inputs to S-boxes are identical so their output di erences are zero. Finally, the output di erence out = (ÆA; 0), shown in Figure 3.26.
Consider the XOR pro le of S1. Our goal now is to nd a characteristic that feeds a nonzero input di erence into S1 while other input di erences of S2; : : : ; S8 are set to zero. Additionally, the characteristic should work with a high probability. If we have a xed input di erence, then output di erences happen with the probability proportional to the corresponding entries in the XOR pro le. One of the largest entries is 14 and occurs in many places in the table. The rst occurrence is in (3x; 0x). It means that the input di erence 00 00 11 produces the output di erence 00 00. The two nonzero bits on the S1 input have had to pass through the expansion block E so they are duplicated on the input of S2 . The only pair of bits that is not duplicated in other S-boxes is the pair of two middle bits (in the E table marked as bits 2 and 3). So we have to look at rows 00 01 00 = 4x, 00 10 00 = 8x, and 00 11 00 = Cx. The only
3.4 Di erential Cryptanalysis |
125 |
Ωin = ( δ A , 60 00 00 00x )
∆ |
1 = 00 80 82 00 x |
δ |
1 |
= 60 00 00 00x |
|
|
f |
|
|
Ω out = ( δ A |
+ 00 80 82 00 |
, 60 00 00 00 ) |
|
x |
x |
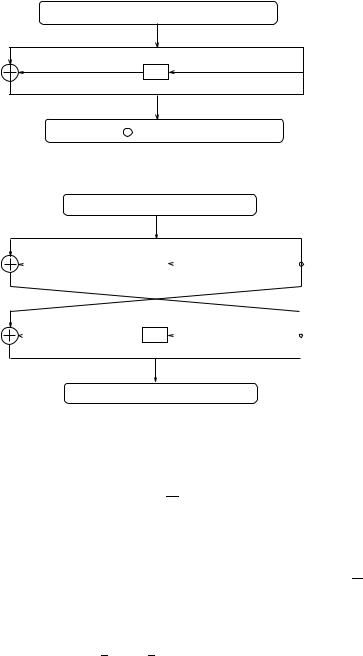
Fig. 3.27. Another single round characteristic of DES
Ω |
in = ( 00 80 82 00 , 60 00 |
00 00 )x |
|||||
∆ 1 = 00 80 82 00 |
|
|
δ |
1 |
= 60 00 00 00 x |
||
|
x |
f |
|
|
|
|
|
∆ 2 |
= 0 |
|
|
δ |
2 = 0 |
|
|
f |
|
|
|||||
|
|
||||||
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
Ωout = ( 60 00 00 00 , 00 00 00 00 )x
Fig. 3.28. A two-round characteristic of DES
row with an entry 14 is the last one Æ = Cx. The pair of di erences (Cx; Ex) happens with probability 1464 . The characteristic is depicted in Figure 3.27. The binary string (00 80 82 00x) is obtained by permuting (E0 00 00 00x) according to the DES permutation block P .
The two single-round characteristics can be concatenated to create 2-round characteristic shown in Figure 3.28. Its probability is 1464 as the second round happens always (with the probability 1).
This informal discussion can be generalized for an arbitrary Feistel-type cryptosystem. The cryptosystem processes n-bit messages and uses a round
n n
function fk : 2 ! 2 . The cryptographic key k is XORed to the inputs of S-boxes.
De nition 3. An m-round characteristic of a Feistel-type cryptosystem is a sequence
126 3 PRIVATE-KEY CRYPTOSYSTEMS
( in; Æ1; 1; : : : ; Æm; m; out) = ( in; ; out)
where in and out are input and output di erences. The pairs (Æi; i); i = 1; : : : ; m, are consecutive input and output di erences for the round function fk.
Characteristics can be concatenated in a similar way as we have done to create
2-round characteristic from two single ones. Let 1 = ( in1 ; 1 ; out1 ) and 2 = ( in2 ; 2 ; out2 ) be two characteristics. They can be concatenated if the swapped
halves of in2 are equal to out1 and the concatenation = ( in1 ; 1;2; out2 ), where 1;2 is the concatenation of the two sequences 1 and 2 .
Any characteristic has a probability attached to it. Let our m-round characteristic be ( in; Æ1; 1; : : : ; Æm; m; out. Then its probability
m
P ( ) = Y pÆii
i=1
where pÆii is the probability that input di erence Æi causes the output di erencei for the function fk in the ith round.
3.4.3 Cryptanalysis of 4-Round DES
First, recall that to be able to recover keys we have to concentrate on the last round. For a given pair of plaintext, we need to know values given to the function fk in the last round. These values are known as they are the right halves of the cryptograms. The main goal is to nd the output di erences which occur on S-boxes in the last round.
We use a characteristic given in Figure 3.26 for ÆA = 20 00 00 00x, which works always (with probability 1). The general scheme of di erences in the
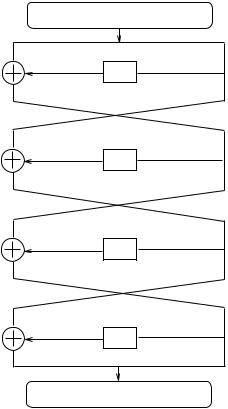
4-round DES is given in Figure 3.29. We start from an observation that |
|
4 = out 2 Æ1: |
(3.5) |
out is known from the cryptograms (left halves) and Æ1 is given from the input (right halves). Take a closer look at 1 and 2. As Æ1 = 0, 1 = 0 as well. On the other hand, Æ2 = 20 00 00 00x so the input di erence on S1 becomes 00 10 00 leaving the rest of the S-boxes with zero di erences (notice that the two middle bits of S1 are not duplicated in other S-boxes by the bit-selection block E). This means that all output di erences of S2; : : : ; S8 are forced to zero { we know di erences on their outputs. Thus 28-bits of 2 are known. From
3.4 Di erential Cryptanalysis |
127 |
Input difference
∆ 1 |
δ |
|
f |
∆ 2 |
δ |
|
f |
∆ 3 |
δ |
|
f |
1
2
3
∆ 4 |
δ |
4 |
|
f |
|
Output difference ( ∆ out ,δ 4 )
Fig. 3.29. Four-round DES
Equation (3.5), we conclude that 28 bits of 4 are known. Being more speci c, we know inputs of seven S-boxes and their output di erences in the last round. By the di erential analysis given in Section 3.4.1, we can nd 7 6 = 42 bits out of the 48-bit key k4 .
To be able to analyze S1 in the 4th round, we need another characteristic. We can use the same one but for ÆA = 04 44 44 44x. As previously, Æ1 = 1 = 0 but Æ2 = 04 44 44 44x. As the input di erence on S1 is zero in the second round, the output di erence on S1 is also zero. From Equation (3.5), the 4-bit di erence on the output of S1 in the 4th round can be determined. Note that the permutation block P behind S-boxes is used in all rounds so the corresponding bits always meet. Once this is done, the missing part of the key can be recovered by the di erential analysis of S1.

128 3 PRIVATE-KEY CRYPTOSYSTEMS
Having the partial key k4, we can strip o the last round and analyze the three round DES. After nding k3, we are left with 2-round DES which can be easily analyzed. The analysis assumes that keys are independent in each round so the introduction of long randomly selected keys for each round does not protect the cryptosystem against the di erential analysis. This is one of very strong advantages of this attack. On the other hand, a \weak" key schedule may allow to deduce the initial key from the partial key used in the last round.
3.4.4 Cryptanalysis of 6-Round DES
Figure 3.30 shows a general scheme of di erences in the 6-round DES. As before, in order to nd the key k6 used in the sixth round, we have to determine the output di erence 6. The following equation can be easily established:
6 = out 4 Æ3 |
(3.6) |
To derive Æ3, we use two 3-round characteristics given in Figures 3.31 and 3.32. The rst characteristic uses
Æ3 = 04 00 00 00x:
is available as it is the di erence of the left halves of the cryptograms. To determine 4, consider Æ4 = 40 08 00 00x. In the fourth round, S-boxes S2,S5,S6,S7,S8 have their input di erences set to zero so their output di erences are forced to zero. This means that we can nd di erences in the sixth round for S2,S5,S6,S7 and S8. This time the analysis of S-boxes is not deterministic due to the fact that Æ4 = 40 08 00 00x occurs with the probability 161 . This of course complicates the analysis as we cannot reduce the set of candidate keys after every observation. Indeed, we need to count all the candidate keys. It is expected that the right key will have a higher frequency than the rest. Thus, after enough observations we can nd 30 bits of k6.
The second characteristic produces Æ4 = 00 20 00 08;
so input di erences in the fourth round are zeroes for S1,S2,S4,S5 and S6. 4 has zero output di erences for these S-boxes. From Equation (3.6), we can nd6 for these S-boxes. By counting keys for S1 and S4, we can determine the corresponding 12 bits of k6. So we know 42 out of 48 bits of k6.

3.4 Di erential Cryptanalysis |
129 |
|
|
Input Difference |
|
∆ |
1 |
δ |
1 |
|
|
f |
|
∆ |
2 |
δ |
2 |
|
|
f |
|
∆ |
3 |
δ |
3 |
|
|
f |
|
∆ |
4 |
δ |
4 |
|
|
f |
|
∆ |
5 |
δ |
5 |
|
|
f |
|
∆ |
6 |
δ |
6 |
|
|
f |
|
Output Difference
Fig. 3.30. Six-round DES
The missing 6 bits of the key (used in S3) can be determined by using 42 already recovered bits. To do this, we rst identify pairs of plaintext/ciphertext which behave according to the characteristic. These pairs are called right pairs. The identi cation can be done by checking if the di erences on the outputs of S-boxes in the fourth round are zeroes. As we know 42 bits of k6, we can generate the corresponding 28 bits of 06 (using the 7th round). Knowing out, we verify whether
06 out = 4 Æ3:
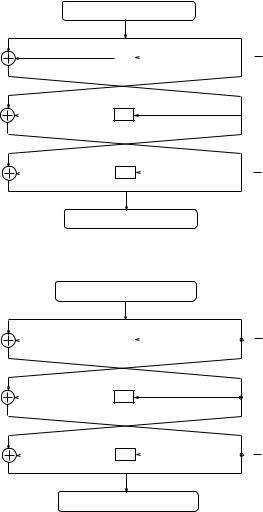
1303 PRIVATE-KEY CRYPTOSYSTEMS
Ω1in = 40 08 00 00 04 00 00 00x
|
40 08 00 00 x |
|
f |
04 00 00 00 x |
|
0 x |
|
0 x |
|
|
|
f |
||
|
40 08 00 00 x |
|
04 00 00 00x |
|
|
|
f |
||
|
Ω 1 |
|
|
|
|
= 40 08 00 00 04 00 00 00 |
|||
|
out |
|
|
x |
Fig. 3.31. First 3-round characteristic
|
Ω |
2in |
= 00 20 00 08 00 00 04 00 x |
||
|
00 20 00 08 x |
|
|
00 00 04 00x |
|
|
f |
||||
|
0 x |
|
|
0 x |
|
|
|
|
f |
||
|
00 20 00 08x |
|
00 00 04 00x |
||
|
|
f |
|||
|
Ω |
2out |
|
|
|
|
= 00 20 00 08 00 00 04 00x |
||||
Fig. 3.32. Second 3-round characteristic
( 14 )
( 1 )
( 14 )
( 14 )
( 1 )
( 14 )
If the equation is not satis ed, we reject the pair as there is an overwhelming probability that this is not the right pair.
For every right pair, we guess the 6-bit part of k6 XORed to the input of S3. Now the 48-bit k6 is used to determine 06. Next we calculate Æ50 = out 06 and verify whether values of di erences on S2, S3, and S8 in the fth round satisfy the equation 5 = Æ4 Æ6. After at most 26 tries, we have all bits of k6. The still missing 56 48 = 8 bits, can be reconstructed by exhaustive search of 28 = 256 possibilities.
