Rivero L.Encyclopedia of database technologies and applications.2006

Figure 3. Path sequences in the example document

<image key="134" source="/cdrom/img1/293.jpeg"> <image><date>

<image><date>" 999010530 " <image></date> <image><colors> <image><colors><histogram>

<image><colors><histogram>" 0.399 0.277 0.344 " <image><colors></histogram> <image><colors><saturation> <image><colors><saturation>" 0.390 " <image><colors></saturation> <image><colors><version> <image><colors><version>" 0.8 " <image><colors></version>

<image></colors>

</image>

and (2) The more high-level DOM interface (W3C, 1998a) provides a standard interface to parse complete documents to syntax trees. In terms of resources, the memory consumption of DOM trees is much higher, linear in the size of the document; thus, it frequently happens that large documents exceed the size of available memory. We propose a bulk load method that has only slightly higher memory requirements than SAX-O(height of document)- but still keeps track of all the contextual information it needs. Thus, the memory requirements of the bulkload algorithm we use are very low as it does not materialize the complete syntax tree.

Since Monet XML stores complete paths, the bulk load routine has to track those paths. We do this by organizing the path summary as a schema tree which we use to efficiently map paths to relations. Each node in the schema tree represents a database relation and contains a tag name and reference to the relation. Figure 3 shows the path sequences generated by combining the SAX events of the parser and a stack in the following way. We attach OIDs to every tag when we put it on the stack. This way, we are able to record all path instances in the documents without having to maintain a syntax tree in (main) memory-an advantage that lets us process very large documents with relatively little memory. The function that performs the actual insertion is insert(R,t) where R is a reference to a relation and t is a tuple of the appropriate type. A first naive approach would thus result in the following sequence of insert statements (disregarding the order in the document and whitespace due to lack of space):

1.insert(sys,(1,image))

2.insert(R(image[key]),(1,“134”))

3.insert(R(image[source]),(1,“/cdrom/img1/

293.jpeg”))

4.insert(R(image/date),(1,2))

5.insert(R(image/date/pcdata),(2,“ 999010530 ”))

6.insert(R(image/colors),(1,3))

Storing XML Documents in Databases

7.insert(R(image/colors/histogram),(3,4))

8.insert(R(image/colors/histogram/pcdata), (4,“ 0.399 0.277 0.344 ”))

9.insert(R(image/colors/saturation),(3,5))

10.insert(R(image/colors/saturation/pcdata),(5,“ 0.390 ”))

11.insert(R(image/colors/version),(3,6))

12.insert(R(image/colors/version/pcdata),(6,“ 0.8 ”))

Database Maintenance

Once data reside in a database, maintenance of these data becomes an important issue. We distinguish between two different maintenance tasks: First, the update of existing data via edit-scripts for propagating changes of source data to the warehouse, and, second, the deletion and insertion of complete versions of documents which may have become stale or need to be added to the warehouse.

The concept of edit-scripts to update hierarchically structured data is both intuitive and easy to implement on modern database systems (Chawathe et al., 1996; Chawathe & Garcia-Molina, 1997). The scripts comprise three basic operations for transforming the syntax tree: insertion of a node, deletion of node, and moving a node. (We do not mention other operators that traverse the syntax tree, see Chawathe & GarciaMolina, 1997; Buneman et al., 1996). We also view these operations as representatives for traversals that are defined in the DOM standard (W3C, 1998a). Continuing our example, an edit script could insert additional subtrees that describe textures in the images or delete items that appear twice in the database. Typically, an edit-script first pins the location of nodes to be changed; this process is often done by navigating through the syntax tree as object identifiers in the database are often not accessible to other applications. Once the location is found, the scripts then apply update, delete, and insert operations. Conceptually, an edit-script may do two kinds of changes: systematic and local changes. Systematic changes may become necessary if a faulty application produced data with errors that are spread over parts of the XML document. In this case, the script traverses large parts of the syntax graph and applies similar changes at various places. In the relational context of our work, this may be an expensive restructuring process. On the other hand, if changes are only local, the script just visits a small number of nodes and patches them. This should be no resource-intensive problem, not in relational, object, or native systems.

We do not have the space to discuss edit-scripts in depth here and refer the reader to the above citations.

Storing XML Documents in Databases

However, we demonstrate their use with an example similar to that used in the performance discussion. Consider again Figure 1. A systematic change would, for example, require us to change all dates from Unix system time, that is, seconds since January 1, 1970 to a more human readable format. The way we go about creating the appropriate edit-script is the following: We look up all associations which assign a value to an attribute unit. Then, for all these nodes, we calculate the new date and replace the old one. Techniques for constructing automata that do the traversal can be found, for example, in Neven and Schwentick (1999). Once such an automaton finds a node n that needs to be updated, it executes an update(n, date, new date format) statement. On the physical data model of the Background section, this is translated into a command that replaces the value of the respective association.

The point that is important for us is that edit-scripts traverse parts of the XML syntax graph and manipulate individual nodes. This is in stark contrast to the second method mentioned above, bulk deletion and reinsertion where we delete a complete segment of the database and reinsert a corrected version. In the example scenario, this means that an individual detector resends the corrected version of a previously submitted document instead of a patching edit-script. Generally, the underlying assumption is that the aforementioned data sources provide the capability of sending both, the edit-script and a complete updated document; however, this assumption holds for many practical applications as well as for our example: a detector may either send an editscript or retransmit a corrected version of the complete document.

It is straightforward to design an algebraic algorithm that does the deletion and visits every node at most once like a linear scan (Schmidt & Kersten, 2002). Still, we need to discuss when to use bulk deletion combined with reinsertion and when to use edit-scripts. The next section looks quantitatively at when to go for what.

Performance Impressions

This section presents performance impressions of a data warehouse (Kersten & Windhouwer, 2000) containing actual features which are more elaborate but similar to the ones used in the running example. The data warehouse uses Monet XML as the physical storage model. A 500 MHz Pentium-class PC running Redhat Linux was our experimentation platform.

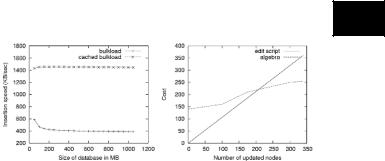
Figure 4 shows the relationship between database size and insertion speed. The figure displays the speedup of an optimized approach with caching over a naive implementation. As one might expect, the insertion into an empty database is faster than into an already densely

Figure 4. Performance of loading and updating data

5

populated one if no intelligent caching is used. As the database gets larger, insertion speed converges to a ratio of about 390 KB/sec. If schema trees are used, bulkload speed more than triples showing the potential of this technique, which has been explained in the Populating the XML Database section. Note that neither bulkload method blocks the database; both operate interactively and do not interfere with the transaction system. Note that the insertion performance in Figure 4 includes converting the textual representation of a document to executable database statements, thus, random memory accesses (which can be alleviated with path caching), whereas deletion can be done as sequential scans.

Updates are considered in Figure 4 as well. Editscripts, as presented in the Database Maintenance section, are run against the database created in the previous experiment; the updates they apply are systematic. The figure plots the performance of edit-scripts against a simple algebraic bulk replacement strategy which consists of deleting those documents that need updating from the database and subsequently loading updated documents into the database. With respect to when to choose which technique, the two lines in Figure 4 show that once more than approximately 220 entries are changed by the edit-script, one should consider reverting to bulk operations for performance reasons. The threshold of 220 entries is surprisingly low; however, one should keep in mind that relational databases are not optimized for pointer-chasing operations. We remark that this threshold also depends on the characteristics of the XML document, especially on the ratio between text and mark-up.

Other Storage Mappings

This section discusses some opportunities and limitations of the methods discussed in this article. It takes up ideas found in the literature and relates them to the techniques we developed for Monet XML.

Positional Mappings and Extent Mappings

Recently, the idea of using the OIDs located on a path as components of a positional number system like the Dewey system caught on (O’Neil et al., 2004; Tatarinov et al., 2002). We can easily adjust the mapping algorithms which produce the Monet mapping to include the whole list of OIDs which are on the stack rather than just include the two lowest ones as the algorithm in the Populating the XML Database section does. This just requires us to look at the complete stack before producing an insertion statement. This kind of positional mapping is especially suited for implementation of query primitives based on tree automata (Comon et al., 1997) since many of the query primitives like axis navigation can be translated transparently to state transitions (Ludäscher, Mukhopadhyay & Papakon stantinou, 2002).

Another type of mapping is called extent mapping. In extent mappings, not only the element OID is recorded but also the range in which the descendant node OIDs can be found; an example of such a mapping can be found in Zhang et al. (2001). The insertion algorithm can be adapted by delaying the generation of an insert statement until, not the start tag of an element, but its end tag is encountered. This way, enough information can be gathered about the position of the end tag.

Semantic Mappings

A semantic mapping in our context is a mapping which takes into account data semantics. For example, a mapping might decide to map an XML element to an instance of a particular datatype. Semantic mappings generally follow two mutually exclusive principles. First, they may analyze schema information such as given by DTDs (Shanmugasundaram et al., 1999) or XML Schema and generate a database schema with features that imitate those found in E/R mappings. This kind of mapping is fully automatic. Second, users may manually specify application-specific constraints that help map document fragments to tuples in relational databases. These mappings try to overcome the semantic gap between XML and relational databases by equipping users with a language to specify which parts of a set of documents correspond to which part of a database schema.

Although semantic mappings are more complex to implement in a streaming manner like the Monet mapping where only a stack is needed to keep track of all necessary information, we can overcome much of the complexity by falling back to conceptually simpler mappings like the Monet mapping or a positional mapping. This is done by implementing the mapping as a two-

Storing XML Documents in Databases

step process. In the first step, the Monet mapping of an incoming XML document is used to derive database relations. In the second step, these relations are combined in database queries to form the semantic entities produced by the semantic mapping. This abstraction can greatly facilitate the complexity of the mapping software.

FUTURE TRENDS

In the future, we are likely to witness a tighter integration of the two paradigms which dominate XML processing: data management and information retrieval. This is likely to pose new challenges with respect to database maintenance and indexing; it is also likely to necessitate new data structures as well as novel query processing and update strategies and will thus require adaptations of the strategies presented in this article.

CONCLUSION

This article discussed performance considerations for typical problems in relational XML document data warehousing, especially the trade-off between algebraic and pointer-chasing algorithms for updates. For practical purposes, it turned out that it often is better to replace a complete database segment and reinsert the updated data than to patch an existing version with expensive edit-scripts. In particular, our experiments showed that once the patched data volume exceeds a small percentage of the database, one should resort to bulk replacement. For good insertion performance, the use of schema trees has been beneficial.

REFERENCES

Buneman, P., Davidson, S.B., Hillebrand, G.G., & Suciu, D. (1996). A query language and optimization techniques for unstructured data. Proceedings of the ACM SIGMOD International Conference on Management of Data, Montreal, Canada (pp. 505-516).

Chamberlin, D., Florescu, D., Robie, J., Siméon, J., & Stefanescu, M. (2001). XQuery: A query language for XML. Retrieved January 29, 2005, from http:// www.w3.org/TR/xquery

Chawathe, S., & Garcia-Molina, H. (1997). Meaningful change detection in structured data. Proceedings of the ACM SIGMOD International Conference on Management of Data (pp. 26-37).

Storing XML Documents in Databases

Chawathe, A., Rajaraman, A., Garcia-Molina, H., & Widom, J. (1996). Change detection in hierarchically structured information. Proceedings of the ACM SIGMOD International Conference on Management of Data (pp. 493-504).

Comon,H.,Dauchet,M.,Gilleron,R.,Jacquemard,F.,Lugiez, D., Tison, S., & Tommasi, M. (1997). Tree automata techniques and applications. Retrieved January 29, 2005, from http://www.grappa.univ-lille3.fr/tata

Deutsch, A., Fernandez, M.F., & Suciu, D. (1999). Storing semistructured data with STORED. Proceedings of the ACM SIGMOD International Conference on Management of Data, Philadephia (pp. 431-442).

Florescu, D., & Kossmann, D. (1999). Storing and querying XML data using an RDBMS. Data Engineering Bulletin, 22(3).

Kersten, M., & Windhouwer, M. (2000). DMW homepage. Retrieved January 29, 2005, from http://www.cwi.nl/~acoi/ DMW/

Klettke, M., & Meyer, H. (2000). XML and object-rela- tional database systems - Enhancing structural mappings based on statistics. International Workshop on the Web and Databases (WebDB) (pp. 63-68).

Ludäscher, B., Mukhopadhyay, P., & Papakonstantinou, Y. (2002). A transducer-based XML query processor.

Proceedings of the International Conference on Very Large Data Bases (pp. 227-238).

Megginson, D. (2001). SAX 2.0: The simple API for XML. Retrieved January 29, 2005, from http:// www.megginson.com/SAX/

Neven, F., & Schwentick, T. (1999). Query automata.

Proceedings of the 18th ACM SIGACT-SIGMOD- SIGART Symposium on Principles of Database Systems

(pp. 205-214).

O’Neil, P., O’Neil, E., Pal, S., Cseri, I., Schaller, G., & Westbury, N. (2004). ORDPATHs: Insert-friendly XML node labels. Retrieved January 29, 2005, from http:// www.cs.umb.edu/~poneil/ordpath.pdf

Roussopoulos, N. (1997). Materialized views and data warehouses. Proceedings of the 4th KRDB Workshop. Retrieved January 29, 2005, from http://SunSITE. Informatik.RWTH-Aachen.DE/Publications/CEUR- WS/Vol-8/

Schmidt, A., & Kersten, M. (2002). Bulkloading and maintaining XML documents. Proceedings of the ACM Symposium on Applied Computing (SAC) (pp. 407-412).

Schmidt, A., Kersten, M., & Windhouwer, M. (2001). Querying XML documents made easy: Nearest concept 5 queries. Proceedings of the IEEE International Confer-

ence on Data Engineering (pp. 321-329).

Schmidt, A., Kersten, M., Windhouwer, M., & Waas, F. (2000). Efficient relational storage and retrieval of XML documents. International Workshop on the Web and Databases, Dallas, Texas (pp. 47-52).

Schmidt, A., Windhouwer, M., and Kersten, M. L. (1999). Feature Grammars. In Proceeding of the International Conference on Information Systems Analysis and Synthesis, Orlando, Florida.

Shanmugasundaram, J., Tufte, K., He, G., Zhang, C., DeWitt, D., & Naughton, J. (1999). Relational databases for querying XML documents: Limitations and opportunities. Proceedings of the International Conference on Very Large Data Bases, Edinburgh, UK (pp. 302-314).

Tatarinov, I., Viglas, S., Beyer, K., Shanmugasundaram, J., Shekita, E., & Zhang, C. (2002). Storing and querying ordered XML using a relational database system. Proceedings of the ACM SIGMOD International Conference on Management of Data (pp. 204-215).

W3C. (1998a). Document object model (DOM). Retrieved January 29, 2005, from http://www.w3.org/DOM/

W3C. (1998b). Extensible markup language (XML) 1.0. Retrieved January 29, 2005, from http://www.w3.org/ TR/1998/REC-xml-19980210

Zhang, C., Naughton, J., DeWitt, D., Luo, Q., & Lohman, G. (2001). On supporting containment queries in relational database management systems. Proceedings of the ACM SIGMOD International Conference on Management of Data.

KEY TERMS

Bulkload: Adding a (large) set of data to a database rather than individual tuples.

Database Maintenance: The task of updating a database and enforcing constraints.

Document Databases: A collection of documents with a uniform user interface.

Document Warehouses: A document database consisting of documents gathered from various independent sources.

INTRODUCTION

Today’s technology allows storing vast quantities of information from different sources in nature. This information has missing values, nulls, internal variation, taxonomies, and rules. We need a new type of data that allow us to represent the complexity of reality, maintaining the internal variation and structure (Bock & Diday, 2000; Diday, 2002, 2003).

In Data Analysis Process or Data Mining, it is necessary to know the nature of null values1, also possible and valid to have some imprecision, due to differential semantics in a concept, diverse sources, linguistic imprecision, element resumed in database, human errors, and so forth (Chavent, 1997; Polaillon, 1998). Thus, we need a conceptual support to manipulate these types of situations. As we are going to see below, symbolic object constitutes a strong conceptual model.

A symbolic object is defined by its intent which contains a way to find its extent. For instance, the description of habitants in a region and the way of allocating an individual to this region is called intent, the set of individuals which satisfies this intent is called extent (Diday, 2003). For this type of analysis, different experts are needed, each one giving concepts.

Basically, Diday (2002) distinguishes between two types of concepts:

1.The concepts of the real world: Defined by an intent and an extent which exist, have existed, or will exist in the real world.

2.The concepts of our mind (among the so called mental objects by Changeux, 1983) which frame in our mind concepts of our imagination or of the real world by their properties and a “way of finding their extent” (by using the senses), and not the extent itself as undoubtedly, there is no room in our mind for all the possible extents (Diday, 2003).

A symbolic object models a concept in the same way our mind does by using a description “d” (representing its properties) and a mapping “a” able to compute its extent, for instance, the description of what we call a car

and a way of recognizing that a given entity in the real world is a car. Hence, whereas a concept is defined by intent and extent, it is modeled by intent and a way of finding its extent by symbolic objects like those in our mind. It should be noticed that it is quite impossible to obtain all the characteristic properties of a concept and its complete extent. Therefore, a symbolic object is just an approximation of a concept, and the problems of quality, robustness, and reliability of this approximation arise (Diday, 2003).

The theme is presented as follows: first, in the Background section, the history and fields of influence and sources of symbolic data. Second, in the main section, formal definitions of symbolic object, semantics applied to the symbolic object concept, and the methods are discussed. Third, future trends are given, followed by conclusions, references, and key terms.

BACKGROUND

Diday presented the first article in 1988, in the Proceedings of the First Conference of the International Federation of Classification Societies (IFCS) (Bock & Diday, 2000). Then, much work has been done up to the publication of Bock and Diday (2000) and the Proceedings of IFCS’2000 (Bock & Diday, 2000; Diday 2003). Diday has directed an important quantity of his PhD thesis, with relevant theoretical aspects for symbolic object. Some of the most representative works are Brito (1991), De Carvalho (1992), Auriol (1995), Périnel (1996), Stéphan (1996), Ziani (1996), Chavent (1997), Polaillon (1998), Hillali (1998), Mfoummoune (1998), Vautrain (2000), Rodriguez Rojas (2000), De Reynies (2001), Vrac (2002), and Pak (2003).

Now, we are going to explain the fundamentals that symbolic objects hold from their fields of influence:2

•Statistics: From statistics, the symbolic object counts. It knows the distributions.

•Exploratory Analysis: The capacity of showing new relations between the descriptors {Tukey, Benzecri}(Bock & Diday, 2000).

•Cognitive Sciences and Psychology: The membership function of the symbolic object is to provide prototypical instances characterized by the most representative attributes and individuals {Rosch} (Diday, 2003).

•Artificial Intelligence: The representation of complex knowledge and the form of manipulation is more inspired from languages based on first order logic {Aristotle, Michalski, Auriol} (Diday, 2003).

•Biology: They use taxonomies and solutions widely investigated in this area {Adamson}(Bock & Diday, 2000).

•Formal Concept Analysis: The complete object symbolic is a Galois Lattice {Wille R.} (Bock & Diday, 2000; Polaillon, 1998).

In some of these sciences, the problem is how to obtain classes and their descriptions (Bock & Diday, 2000)

The symbolic data tables constitute the main input of a symbolic data analysis, helped by the background knowledge (Diday, 2003). In Chapter 1 of Bock and Diday’s book are mentioned as follow: each cell of this symbolic data table contains data of different types:

a.Single quantitative value: if « height » is a variable and w is an individual: height (w) = 3.5.

b.Single categorical value: Town (w) = Tandil.

c.Multivalued: in the quantitative case height (w) = {3.5, 2.1, 5} means that the height of w can be either 3.5 or 2.1 or 5.

d.Interval: height (w) = [3, 5], which means that the height of w varies in the interval [3, 5].

e.Multivalued with weights: for instance a histogram or a membership function (possibility, beliefs, or capacity theory can be also applied). Variables can be:

a.Taxonomic: the color is considered to be light if it is white or pink.

b.Hierarchically dependent: we can describe the kind of computers of a company only if it has a computer; hence, the variable “does the company have computers?” and the variable “kind of computers” are hierarchically linked.

c.With logical dependencies: if age (w) is less than 2 months, then height (w) is less than 10.

Example: We need to model the concept of each airline company. We have stored Tables 1 and 2.

Symbolic data are generated when we summarize huge sets of data. The need for such a summary can appear in

Symbolic Objects and Symbolic Data Analysis

Table 1. Travel

Table 3. Symbolic table, modeling the concept of company

different ways, for instance, from any query to a database, which induces categories and descriptive variables. Symbolic data can also appear after a clustering in order to describe in an explanatory way (by using the initial variables) the obtained clusters (Diday, 2003; Bock & Diday, 2000).

Symbolic data may also be “native” in the sense that they result from expertise knowledge (type of emigration, species of insects), probable distribution, percentages, or range of any random variable associated with each cell of a stochastic data table, time series, confidential data, and so forth. Also, they result from relational databases in order to study a set of units whose description needs the merging of several relations (Diday & Billard, 2002).

Symbolic Objects and Symbolic Data Analysis

SYMBOLIC OBJECT AND SYMBOLIC DATA ANALYSIS

Symbolic Object:

Formal Definitions

A Symbolic Object is a triple s = (a, R, d) where R is a relation between descriptions, d is a description and “a” is a mapping defined from Ω in L depending on R and d. (Diday, 2003)

Most of the symbolic data analysis algorithms give in their output the symbolic description “d” of a class of individuals by using a generalization process. By starting with this description, symbolic objects give a way to find, at least, the individuals of this class. Example: The age of two individuals w1, w2 are age(w1) = 30, age(w2) = 35; the description of the class C = {w1, w2} obtained by a generalization process can be [30, 35]. In this simple case, the symbolic object “s” is defined by a triple: s = (a, R, d) where d = [30, 35], R = “ ” and “a” is the mapping: Ω → {true, false} such that a(w) = the true value of age(w) R d denoted [age(w) R d]. An individual w is in the extent of s iff a(w) = true (Diday, 2002).

There are two kinds of symbolic objects:

•Boolean Symbolic Objects: The instance of one binary relation between the descriptor of the object and the definition domain that is defined to have values true or false. If [y (w) R d] = {true,

false}, then it is a Boolean symbolic object (Diday, 2002, 2003). Example: s=(color {red, white}), here we are describing an individual /class whose color is red or white.

•Modal Symbolic Objects: In some situations, we can’t say true or false, we have a degree of belonging, or some linguistic imprecision as always true, often true, fifty-fifty, often false, always false;

now we say that the relation is fuzzy. If [y (w) R d]L = [0,1] is a modal symbolic object (Diday,

2003; Diday & Billard, 2002). Example: s=(color[(0,25) red, (0,75) white]), at this point we are describing an individual/class that has color: 0,25 red; 0,75 white. This weighs can have different meaning, which are going explain to below.

Diday called assertion a special case of a symbolic object defined by s = (a, R, d) where R is defined by [d’ R d] = i =1, p [d’i Ri di] where “ ” has the standard logical meaning and “a” is defined by: a(w) = [y(w) R d] in the Boolean case. Notice that considering the expression a(w) = i =1, p [ yi (w) Ri di], we are able to define the symbolic object s = (a, R, d) (Diday, 2002; Diday & Billard, 2002).

The extension of a symbolic object is a function that permits us recognize when an individual belongs the 5 class description.

In the Boolean case, the extent of a symbolic object is denoted Ext(s) and defined by the extent of a, which is: Extent (a) = {w Ω / a (w) = true}. In the modal instance, given a threshold α, it is defined by Extα (s)= Extentα (a)= {w Ω / a (w) ≥ a} (Diday, 2002; Diday & Billard, 2002).

Semantics Applied to the Symbolic Object Concept

The semantics are applied in the modal symbolic objects and are the weights observed in the previous example of this type of symbolic object (Bock & Diday, 2000):

•Probabilities: This is the classical situation; Kolmogorov’s axiom:

Pr(E1 U E2)= Pr(E1) + Pr(E2) - Pr(E1 )∩E2)

•Capacities: At this point, there are groups with probabilistic multinomial variables. The capacity is interpreted in Choquet’s sense: “The probability of at least one individual belongs this value”, the capacity of a modality is the union capacity.

Consequently, the capacity of SO1 and SO2 for M1 is p11 + p21 - p11 * p21, and the capacity of SO1, SO2, …, SOn for M1 is computed using the associative property.

•Possibilities: When the frequency theory fails. Example: We have a math book, but the word mathematics appears few times. The mathematician knows what this book is about. In this situation, we need different experts to give us their experience. So Zadeh’s axiom is used for fuzzy sets:

Pos(E1 U E2)= Máx.( Pos(E1), Pos(E2))

•Beliefs: Here, the expert says: “I think that the probability of the occurrence of A is p1, p2 is B, but I do not know everything of A and B“. If p1 + p2 < 1, then 1 - (p1 + p2) expresses his ignorance. Schaffer’s axiom (Bender, 1996):

Bel(E1 U E2) ≥ Bel(E1) + Bel(E2) - Bel(E1 )∩E2)

Dumpster’s rule allows combining the beliefs of various experts.

We can see that in these theories emphasis falls mainly on the knowledge of the expert. The first two

theories work with empirical information; the last ones have a higher level of information based on concepts.

The Methods

In the article “An Introduction to Symbolic Data Analysis and the Sodas Software” Diday (2002) presents the main characteristics for the methods by the following principles:

1.They start as input with a symbolic data table, and they give as output a set of symbolic objects. These symbolic objects give explanation of the results in a language close to the one of the user.

2.They use efficient generalization processes during the algorithms in order to select the best variables and individuals.

3.They provide graphical descriptions taking into account the internal variation of the symbolic objects.

We prepared a table to give an idea about the methods implemented in Sodas3.

Symbolic Objects and Symbolic Data Analysis

methods to a new kind of data table, called symbolic data table, and to give more explanatory results expressed by real-world concepts mathematically represented by easily readable symbolic objects (Diday & Billard, 2002; Bock & Diday, 2000).

Some advantages are: It preserves the confidentiality of the information; supports the initial language in which they were created; allows the spread of concepts between databases. Independent from the initial table, they are capable of identifying some individual coincidence described in another table (Bock & Diday, 2000; Diday, 2003).

As a result of working with higher units, called concepts, necessarily described by more complex data extending data mining to knowledge mining (Diday, 2004).

The concept of symbolic object is very important for the construction of the data warehouse, and it is an important development for data mining, especially for the manipulation and analysis of aggregated information.

Table 4. Methods in Sodas software

FUTURE TRENDS

The most important features incorporated in software Sodas24 are: neuronal networks, regression, multidimensional scaling, mixture decomposition, Kohonen maps, and propagation of the obtained symbolic objects. Some of the most recent advances are mixture decomposition of distributions of distributions (by Copulas, Dirichlet, and Kraft, stochastic process), stochastic symbolic, conceptual lattices using capacity theory, symbolic class description and symbolic regression (Diday, 2002, 2004).

Future investigations and applications are oriented to spatial symbolic clustering by pyramids, symbolic time series, consensus between different descriptions of the same set of units (Diday, 2004).

CONCLUSION

The need to extend standard data analysis methods (exploratory, clustering, factorial analysis, discrimination, and so forth) to symbolic data tables in order to extract new knowledge is increasing due to the expansion of information technology, now able to store an increasingly larger amount of huge data sets. This requirement has led to a new methodology called symbolic data analysis whose aim is to extend standard data analysis

Symbolic Objects and Symbolic Data Analysis

REFERENCES

ASSO. Project home page. Retrieved July, 2004, from http://www.info.fundp.ac.be/asso/

Auriol, E. (1995). Intégration d’approches symboliques pour le raisonnement à partir d’exemples. Thèse de Doctorat, Université Paris 9 Dauphine, France.

Bender, E. (1996). Mathematical methods in artificial intelligence. IEEE Computer Society Press.

Bock, H.H., & Diday, E. (2000). Analysis of symbolic data. Studies in classification, data analysis and knowledge organization. Springer Verlag.

Bravo, C. (2002, July). Strata decision tree: A symbolic data analysis technique. Workshop Symbolic Data Analysis. Cracow University of Economics. CRACOW (Poland). Retrieved July, 2002, from http:// www.jsda.unina2.it/WorkSDA/BravoWSDAfinal.pdf

Brito, P. (1991). Analyse de données symboliques. Pyramides de d’héritage. Thèse de Doctorat, Université Paris 9 Dauphine, France.

Brito, P. (2001). Hierarchy and pyramid clustering. ASSO Meeting Paris 2001. Retrieved August, 2002, from http:/ / w w w - r o c q . i n r i a . f r / s o d a s / W P 6 / W P 6 . 1 - Dauphine2001_fichiers/v3_document.htm

Chavent, M. (1997). Analyse des Données symboliques.

Une méthode divisive de classification. Thèse de doctorat in Sciences. I’Université Paris IX-Dauphine. Retrieved September, 2002, from http://www.math.u-bordeaux.fr/ ~chavent/thesemc.ps

Chavent, M. (1998). A monothetic clustering method. Pattern recognition letters. 989-996. Retrieved August, 2002, from http://www.math.u-bordeaux.fr/~chavent/ PRL98.ps

De Carvalho, F. (1992). Méthodes descriptives en analyse des données symboliques. Thèse de Doctorat in Informatique des Organisations, Université Paris 9 Dauphine, France.

De Reynies. (2002). Classification et discrimination en analyse de données symboliques: Application à l’exploitation de scénarios d’accidents routiers. Thèse de Doctorat, Université Paris 9 Dauphine, France.

Diday, E. (2002). An introduction to symbolic data analysis and the Sodas software. The Electronic Journal of Symbolic Data Analysis, 0, 000-000. Retrieved Devember, 2002, 2005, from http://www.jsda.unina2.it/volumes/Vol0/ Edwin.pdf

Diday, E. (2002, July). The future of symbolic data analy-

sis. Workshop Symbolic Data Analysis. Cracow Univer- 5 sity of Economics. CRACOW (Poland). Retrieved Novem-

ber 2002, from http://www.jsda.unina2.it/WorkSDA/ DidayWSDA.pdf

Diday, E. (2003, September 3-6). Concepts and Galois lattices in symbolic data analysis. Journées de l’Informatique Messine. Knowledge Discovery and Discrete Mathematics Metz, France. Retrieved October, 2003, from http://www.inist.fr/uri/jim03/diday.pdf

Diday, E. (2004, January). From data mining to knowledge mining: Symbolic data analysis and the Sodas software.

Proceedings of the Workshop on Applications of Symbolic Data Analysis, Lisboa, Portugal. Retrieved November, 2003, from http://www.info. fundp.ac.be/asso/dissem/ W-ASSO-Lisbon-Intro.pdf

Diday, E., & Billard, L. (2002). Symbolic data analysis: Definitions and examples. Retrieved May, 2004, from h t t p : / / w w w . s t a t . u g a . e d u / f a c u l t y / L Y N N E / tr_symbolic.pdf

Espósito, F., Malerba, D., Gioviale, V., & Tamma, V. (2001). Comparing dissimilarity measures for symbolic data analysis. Proceedings of the Joint Conferences on New Techniques and Technologies for Statistics and Exchange of Technologies and Know-How

(pp. 473-481). Retrieved November, 2002, from http:// www.di.uniba.it/~malerba/publications/ntts-asso.pdf

Gettler-Summa, M. (2000). Marking and generalization by symbolic objects in the symbolic official data analysis software. Proceedings of the 4th European Conference on Principles and Practice of Knowledge Discovery in Databases, Lyon, France, September. Retrieved January, 2003, from http://eric.univ-lyon2.fr/~pkdd2000/Down- load/WS6_8.pdf

Hebrail, G., & Lechevallier, Y. (2000). DB2SO: A software for building symbolic objects from databases. Retrieved October, 2002, from http://www-rocq.inria.fr/ axis/papers/00smpa/hebrail.pdf

Hillali Y. (1998). Analyse et modélisation des données probabilistes: Capacités et lois multidimensionnelles.

Thèse de Doctorat, Université Paris 9 Dauphine, France

Lauro, C., & Palumbo (2000). Principal component analysis of interval data: A symbolic data analysis approach.

Computational Statistics, 15(1), 73-87.

Mfoummoune, E. (1998). Aspects algorithmiques de la classification ascendante pyramidale. Thèse de Doctorat, Université Paris 9 Dauphine, France.