Rivero L.Encyclopedia of database technologies and applications.2006

Assume, for instance, entities Person and Book, and a relationship Author between them. The relationship is many-to-many, as some books have several authors, and some authors have written several books. However, we would like the relationship to be ordered since it may be important for an application to know which one is the first book of an author, the second, and so forth. Note that the order is implicit and enforced on the XML side; hence, no special notation is needed to signal it.

TRANSLATING THE EXTENDED MODEL

Assume that we have an extended E-R model in which, besides the usual E-R constructs (entity types, relationships, attributes, relationship constraints), we also have categories, covering and overlap constraints (on categories and roles), recursive relationships, and ordered relationships. How would such a model get translated into XML? Here we offer a translation, including several options that are up to the translator:

•For each entity type E, create an element tr(E);

•For each attribute in the entity type, create an attribute or a simple subelement;

•For each one-to-many relationship R between entity types E1 (many side) and E2 (1 side),

•Option 1: make tr(E2) a subelement of tr(E1);

•Option 2: add an ID attribute to the tr(E1), and IDREF attribute to tr(E2);

•Option 3: add a primary key to tr(E1), and a foreign key to tr(E2);

•On each case, add all attributes of R as attributes or subelements of tr(E2) too.

•For each many-to-many relationship R between entity types E1 and E2,

•Create a new element E; use IDs and IDREFs or key and primary keys to establish relationships between E and tr(E1) and E and tr(E2);

•Add all attributes of R as attributes or simple subelements of E.

•For any relationship R involving entity types E1,…,En

•Create a new element E; use IDs and IDREFs or key and primary keys to establish binary relationships between E and tr(E1), E and tr(E2),…, E and tr(En);

Semistructured Data and its Conceptual Models

•Add all attributes of R as attributes or simple subelements of E.

•For each recursive relationship R on entity type E,

•Add the name of tr(E) as a subelement of tr(E) (repeated subelement, if R is one-to-many).

•For each category C, made up of entity types E1 and E2,

•Create an element tr(C), defined as (tr(E1)| tr(E2)) (i.e., a choice).

Some comments are in order about this translation. When dealing with one-to-many relationships, several options are offered. Observe that if one chooses to represent such relationship using subelements and the entity type being represented as a subelement is involved in other relationships, redundancy may occur. Assume, for instance, entity types Employee, Department, and Project such that relationship Works-for is one-to-many between Employee and Department, and Manages is one-to-many between Employee and Project. We can declare Employee a subelement of Department, or a subelement of Project, but should not do both. If we choose to declare Employee a subelement of Department, Option 2 or Option 3 should be used to model Manages (Lee, Mani & Chu, 2003).

As for many-to-many relationships, no options are offered. Such relationships are modeled by reification, that is, converting the relationship into an element as if it were another entity type. This is similar to what happens when E-R models are captured in ODL (Catell, 1997) and is the only acceptable solution to avoid redundancy and possible inconsistencies. Finally, for n-ary relations (n > 2), the solution adopted is similar. However, it could be possible to produce more stylized designs by analyzing the relationship. The solution proposed is correct, but other options are also available. For instance, consider a ternary relationship Supplies between entity types Company, City, and Product. Then we can create elements Company, Product, City, and element Supply such that Supply is a subelement of Company, and it contains IDREFS or foreign keys for the IDs or primary keys for both Product and City (Mani, Lee & Muntz, 2001).

As for recursive relationships, note that if a relationship R on entity type E is not recursive (as in our example of relationship Married on entity type Person), one should treat it as a binary relationship and literally follow the rules for binary relationships. Note that there is no need to do anything about ordered relationships. Order is an implicit part of the XML data model.

With respect to categories, two points are important. First, by default, the translation given assumes that the

Semistructured Data and its Conceptual Models

category is covering and non-overlapping; when this is not the case, the translation must be made a bit more complex. If the category is non-covering, then the union itself has to be considered part of a union. Assume a category Owner, made up of entities Bank and Person, and assume not all owners are banks or persons. The owner can be modeled as an element Owner with a union (Bank | Person | Other). Note that element Other may have no attributes or subelements. If the category is overlapping, a third choice must be given for overlapping objects that has all the attributes of the other elements. Assume a category Person which is made up of entity types Student and Staff; the category is overlapping (that is, some persons are both students and staff). Let attr(E) be the attributes of entity type E. Then Person can be represented as the union of three subelements, Student (with attributes att(Student)), Staff (with attributes attr(Staff)), and Student-Staff (with attributes attr(Student) U attr(Staff)). Second, some further processing is also possible. If C is both a covering and non-overlapping category, it is possible to dispense with creating elements for E1 and E2. Instead, if attr(E1) denotes all subelements of E1 and attr(E2) all subelements of E2, we can create an element tr(C) and define it as (attr(E1) | attr(E2)). When neither E1 nor E2 are involved in any relationships, this is all that is needed. If either one is involved in a relationship, we need to make sure the tr(E1) (or tr(E2)) have either an ID or a primary key that can be used to represent the relationship.

FUTURE TRENDS

We have emphasized here notions that seem necessary to model semistructured (XML) data; in particular, it seems clear that the idea of category and the expression of set constraints are needed if we are to use all the power of XML. Future research will have to focus on the issue of adding such constructs to conceptual models, as well as examining the need to develop specific ways to capture the irregular nature of semistructured data.

CONCLUSION

It must be pointed out that some authors have argued that other data models are more suited than E-R for representing semistructured data (see Bird, Goodchild & Halpin, 2000; Conrad, Scheffner & Freytag, 2000). However, as far as the authors are aware, neither UML nor ORM can represent the set constraints (such as covering and overlap constraints) discussed in this entry, although they seem to be able to represent more constraints than E-R models. Given this, we believe that we need to propose

extensions to UML and ORM similar to that of covering

and overlap constraints before we can use them as a 5 conceptual model for XML. Also, since UML and ORM

lack a formal semantics, it is impossible to ascertain with any certainty what the models can and cannot do. On the other hand, E-R has a well defined formal semantics, which allows us to specify the type of constraints it is missing.

REFERENCES

Badia, A. (2002). Conceptual modeling for semistructured data. Proceedings of the International Workshop on Data Semantics in Web Information Systems (DASWIS).

Bird, L., Goodchild, A., & Halpin, T.A. (2000). Object role modeling and XML schema. Proceedings of the 19th International Conference on Conceptual Modeling.

Bodart, F., Patel, A., Sim, M., & Weber, R. (2001). Should optional attributes be used in conceptual modeling? A theory and three empirical tests. Information Systems Research, 12(4), 384-405.

Bray, T., Paoli, J., & Sperberg-McQueen, C.M. (Eds). (2004). Extensible markup language (XML) 1.0, W3C recommendation. Retrieved February 2, 2005, from http:// www.w3.org/TR/REC-xml-20001006

Catell, R. (Ed). (1997). The object database standard: ODMG 2.0. Morgan Kaufmann.

Chen, P. (1976). The entity-relationship model: Toward a unified view of data. ACM Transactions on Database Systems, 1.

Conrad, R., Scheffner, D., & Freytag, J.C. (2000). XML conceptual modeling using UML. Proceedings of ER 2000 (pp. 558-571).

Date, C. (2000). An introduction to database systems.

Addison-Wesley.

Davis, F. (1993). Requirement specification: Objects, functions and states. Prentice Hall.

Elmasri, R., Weeldreyer, J.A., & Hevner, A.R. (1985). The category concept: An extension to the entity-relationship model. International Journal on Data and Knowledge Engineering, 1(1).

Elmasri, R., Wu, S., Hojabri, B., Fu, J., & Li, Q. (2002). Conceptual modeling for customized XML schemas. Proceedings of the ER’02 Conference.

Halpin,T.A.,&Bloesch,A.(1999).DatamodelinginUMLand ORM: A comparison. Journal of Database Management.

Lee, D., Mani, M., & Chu, W.W. (2003). Schema conversion methods between XML and relational models. Knowledge Transformation for the Semantic Web, 1-17.

Mani, M., Lee, D., & Muntz. R.R. (2001). Semantic data modeling using XML schemas. Proceedings of ER(pp. 149-163).

Rumbaugh, J., Jacobson, I., & Booch, G. (1999). The unified modeling language reference manual. AddisonWesley.

Thalheim, B. (2000). Entity-relationship modeling.

Springer-Verlag.

KEY TERMS

Category: Special type of entity that represents the union of two or more different entity types.

Conceptual Model: Semiformal framework (usually a language and a diagram notation) used to capture information about the structure and organization of things, properties, and relations in a fragment of the real world, called the domain, usually one of interest to a (software) system. The model represents the semantics of the domain to the system.

Conceptual Modeling: Starting point for database design that consists of producing a conceptual model.

Covering Constraint: Constraint that states that the entity types that compose a category, taken together, contain all the elements of the category.

Semistructured Data and its Conceptual Models

Entity-RelationshipModel:Oneofthemostwellknown and widely used conceptual models. The main concepts in the ER model are entity types, relationships, and their attributes.

Overlap Constraint: Constraint that states that the entity types that compose a category can (or cannot) have elements in common.

Semistructured Data: Data that does not adjust to a predefined schema or that has a very flexible, possibly dynamic, schema.

XML: Extensible Markup Language, a sublanguage of SGML that provides a way to structure and format data, especially in textual form. The data is represented as XML documents; an XML document may have an optional schema associated with it. XML is considered a semistructured data model because a schema is not always necessary, and even if a schema is present, it could be quite flexible.

ENDNOTE

1This translation still leaves open one important question: whether to model attributes in E-R models as attributes in XML or as simple subelements. However, this decision is not relevant for the structural issues we are discussing.

Reynold Cheng

Purdue University, USA

Sunil Prabhakar

Purdue University, USA

INTRODUCTION

Sensors are often used to monitor the status of an environment continuously. The sensor readings are reported to the application for making decisions and answering user queries. For example, a fire alarm system in a building employs temperature sensors to detect any abrupt change in temperature. An aircraft is equipped with sensors to track wind speed, and radars are used to report the aircraft’s location to a military application. These applications usually include a database or server to which the sensor readings are sent. Limited network bandwidth and battery power imply that it is often not practical for the server to record the exact status of an entity it monitors at every time instant. In particular, if the value of an entity (e.g., temperature, location) monitored is constantly evolving, the recorded data value may differ from the actual value. Querying the database can then produce incorrect results. Consider a simple example where a user asks the database: “Which room has a temperature between 10oF and 20oF?” If we represent temperature values of rooms A and B stored in the database by A0 and B0 respectively, we can see from Figure 1(a) that the answer to the user query is “Room B”. In reality, the temperature values of both rooms may have changed to newer values, A1 and B1, as shown in Figure 1(b), where the true query answer should be “Room A”. Unfortunately, because of transmission delay, these newest pieces of information are not propagated in time to the system to supply fresh data to the query, and consequently the query is unable to yield a correct answer.

In general, the incorrectness of query results is due to sensor uncertainty, an inherent property of any sensor database where each recorded data item is only an older, approximate version of the corresponding entity monitored. Apparently, providing meaningful answers in face of sensor uncertainty appears to be a futile exercise. In many situations, however, the values of sensors cannot change drastically in a short period of time – the degree and/or rate of change of a sensor value

Figure 1. Example of data uncertainty and a range query for temperature values

is constrained. This helps us to alleviate the problem. In the previous example, if we can guarantee that the actual temperatures of room A and B are no more than some deviations from A0 and B0 respectively, as in Figure 1(c), then we can state with confidence that room A does not satisfy the query.

Whether room B satisfies the query is less obvious. In Figure 1(c), it is not clear whether B has a temperature between 10oF and 20oF. However, the fact that the uncertainty associated with B’s temperature is bounded makes it possible to decide the degree of likelihood that B satisfies this query. In general, bounded uncertainty allows us to augment different levels of confidence with each answer (e.g., as a probability), instead of providing a definite answer. Queries that augment answers with probability values, based on uncertain information, are known as . In the previous example, a probabilistic query produces answers such as: “Room A has a probability of 0 being between 10oF and 20oF, while Room B has a probability of 0.7”. Contrast with a query that gives incorrect answers because of stale data, a probabilistic query provides more confidence in the answers since uncertainty is considered.

Depending on the nature of the probabilistic query, confidence in a probabilistic query answer can be expressed in different forms. We will study different classes of probabilistic queries, which have different

forms of answers and evaluation techniques. We also examine the concept of “quality” of a probabilistic query result which is related to the ambiguity of the result.

The rest of this article is organized as follows. We first present the background and related works. Then we examine in detail how sensor data uncertainty can be modeled. Based on the data models, we present a classification of probabilistic queries. For each query class, we examine factors that determine quality of probabilistic query answers. Finally, we outline future research issues.

BACKGROUND

Approximate answers to queries based on a subset of data have been well studied. Vrbsky and Liu (1994) studied approximate answers for set-valued queries (where a query answer contains a set of objects) and single-valued queries (where a query answer contains a single value). An exact answer E can be approximated by two sets: a certain set C which is the subset of E, and a possible set P such that C P is a superset of E. Other techniques like precomputation (Poosala & Ganti, 1999), sampling (Gibbons & Matias, 1998), and synopses (Acharya, Gibbons, Poosala & Ramaswamy, 1999) are used to produce statistical results. While these efforts investigate approximate answers based on a subset of (exact) values of the data, this article addresses imprecise answers that assume all (uncertain) values of the data.

There are a number of works about evaluation of intervals. Olston et al. discuss the problem of balancing the trade-off between precision and performance for querying replicated data (Olston, Loo & Widom, 2001; Olston & Widom, 2000, 2002). In their model, the cache in the server cannot keep track of the exact values of sensor sources due to limited network bandwidth. Instead of storing the actual value in the server’s cache, an interval for each item is stored, within which the current value must be located. A query is then answered by using these intervals, together with the actual values fetched from the sources. The problem of minimizing the update cost within an error bound specified by aggregate queries is studied.

Probabilistic range querying over uncertainty of moving objects is presented by Wolfson, Sistla, Chamberlain, and Yesha (1999). Cheng, Kalashnikov, and Prabhakar (2004) present a solution for probabilistic nearest neighbor queries over moving objects. A generalized taxonomy of uncertainty models is presented by Cheng and Prabhakar (2003). Evaluation techniques and quality metrics are studied by Cheng, Kalashnikov, and Prabhakar (2003).

SENSOR UNCERTAINTY MODELS

Uncertainty of sensor values can be represented in three forms, from no attention to uncertainty at all, to the highest resolution of uncertainty information (Cheng & Prabhakar, 2003). For notational convenience, let us assume that a real-valued attribute a of a set of database objects T is queried. We name the ith object of T as Ti, and the value of a for Ti as Ti.a (where i = 1,…, |T|).

1.Point Uncertainty: This is the simplest model, where we assume there is no uncertainty associ-

ated with data at all. Each data item, Ti.a, is supposed to be a correct representation of the external entity being monitored. Queries use these exact values to evaluate results. Although manipulating real values is relatively easy for a query, the example in Figure 1 illustrates how such data can lead to incorrect query results.

2.Interval Uncertainty: Instead of representing the exact sensor value in the database, an uncer-

tain interval, denoted by Ui(t), is stored. Specifically, Ui(t) is a close interval [li(t),ui(t)], where li(t) and ui(t) are real-valued functions of t, bounding the value of Ti.a at time t. This model represents imprecision of data in the form of an interval. An

example model of Ui(t) is an interval bounding all values within a distance of (t-tupdate) r of Ti.a, where tupdate is the time that Ti.a is last updated, and r is the current rate of change of Ti.a. Thus, Ui(t) expands linearly with time until the next update of

Ti.a is received. Another realization of this model can be found in Wolfson et al. (1999).

3.Probabilistic Uncertainty: This model is proposed by Cheng et al. (2003). Compared with interval uncertainty, it requires one more piece of information – the probability density function (pdf) of Ti.a within Ui(t). We call this function an uncer-

tain pdf of Ti.a at time t, denoted by fi(x,t). Notice

Further, the exact form of fi(x,t) is applicationdependent. For example, in modeling sensor measurement uncertainty, where each Ui is an error range containing the mean value, fi(x,t) can be a normal distribution around the mean value. Another example is the modeling of one-dimensional moving objects, where at any point in time, the actual location is within a certain bound, d, of its last reported location value. If the actual location changes further than d, then the sensor reports its new location value to the database and possibly changes d. Then Ui(t) contains all the values within

a distance of d from its last reported value (Wolfson et al., 1999), and fi(x,t) can be a uniform distribution, that is,

fi(x,t )= 1/[ ui(t) - li(t)] for Ti.a Ui(t)

which models the scenario when Ti.a has an equal chance of locating anywhere in Ui(t). Alternatively, one may perform an estimation of the pdf based on time-series analysis, the discussion of which is beyond the scope of this article, and interested readers are referred to Chatfield (1989) for details.

As we can see, the probabilistic uncertainty model is the most complicated model of sensor uncertainty among the ones we presented. The complexity of the model is paid off, however, by the fact that probabilistic queries can be defined, which we discuss in the next section.

CLASSIFICATION OF PROBABILISTIC QUERIES

A probabilistic query assumes that data inputs are characterized under the probabilistic uncertainty model and augments the answers with confidence, expressed in probability values. In this section, we examine different types of probabilistic queries. In particular, we present a classification scheme of probabilistic queries proposed by Cheng et al. (2003).

Probabilistic queries can be classified in two ways.1 First, we can classify them according to the forms of answers required. An entity-based query is one that returns a set of objects (e.g., list of objects that satisfy a range query), whereas a value-based query returns a single numeric value (e.g., value of a particular sensor). Another criterion is based on whether an aggregate operator, such as SUM and MAX, is used to produce results. An aggregate query is one where interplay between objects determines the results. For example, to decide whether an object holds the minimum value of Ti.a requires us to examine other objects as well. In contrast, for a non-aggregate query, the suitability of an object as the result to an answer is independent of other objects. A range query is a typical example-whether an object satisfies the range query is not affected by the values of other objects.

Based on this classification, we obtain four classes of probabilistic queries. For the names of the queries defined, the first letter is either E for entity-based query or V for value-based query.

1.Value-Based Non-Aggregate Class: This query class returns a single value for a given object as the

only answer and does not involve any aggregate operations. An example is the probabilistic single 5 value query (VSingleQ), which returns the probabilistic uncertainty information (i.e., Ui(t) and fi(x,t))

of a given object Ti.

2.Entity-Based Non-aggregate Class: This query class returns a set of objects, where the satisfiability of each object to the query is independent of others. One such query is the probabilistic range query (ERQ): given a closed inter-

val [l,u], a list of tuples (Ti,pi) are returned, where pi is the non-zero probability that Ti.a [l,u].

3.Entity-Based Aggregate Class: In this query class, an aggregate operator is involved, and a set of objects together with their probability values, that is, a list of n tuples (Ti,pi) is returned, with

∑in=1 pi = 1 . A typical example is the probabilistic

minimum query (EMinQ): a set of tuples (Ti,pi) are returned, where pi is the non-zero probability that Ti.a is the minimum among all items in T.

4.Value-Based Aggregate Class: An aggregate operation is involved in deciding a single value to

be returned. As an example, a probabilistic sum query (VSumQ) yields l,u as well as {p(x) | x [l,u]}, where X is a random variable for the sum of values of a for all objects in T, and p(x) is

u

a pdf of X such that ∫ p(x)dx = 1.

l

This classification scheme allows us to develop evaluation algorithms for different types of probabilistic queries. Consider the evaluation of an ERQ. Since each object Ti can be evaluated independently of other objects, we first compute the overlapping interval OI of the two intervals, Ui(t) and [l,u]. The probability that Ti satisfies the ERQ, that is, pi, is then calculated by integrating fi(x,t) over OI. On the other hand, evaluating an EMinQ requires a completely different algorithm, details of which can be found in Cheng et al. (2003).

QUALITY OF PROBABILISTIC

RESULTS

As mentioned before, a probabilistic query returns answers augmented with probability values, as opposed to definite answers produced by a traditional query. A certain degree of imprecision is incorporated into the query answer, expressed in the form of probability values. The imprecision of a query answer is due to the fact that data supplied to the probabilistic query are inherently uncertain. In particular, if the data interested to a query contain a lot of uncertainty (e.g., their

Figure 2. Uncertainty and quality of results. In (a), it is not clear which item has a dominant probability value of satisfying EMinQ, and the quality of the result is poor. In (b), item D has a higher chance of satisfying EMinQ, yielding a higher quality result.

uncertain intervals are large), a probabilistic query can yield ambiguous answers which may not be very useful to the user. Figure 2(a) shows four items with large uncertain intervals that overlap each other. Assume these items have the same uncertain pdf. We can see that it is difficult to decide which item has a larger chance of being the minimum: the probability that satisfies the EMinQ is roughly the same for the four items. The quality of the result to this EMinQ is said to be “poor”, since it gives a vague answer and reflects that there is too much uncertainty for the query to yield a reasonable answer. On the contrary, the uncertainty intervals in Figure 2(b) are smaller, and apparently item D has a higher probability of having the minimum value, yielding a better quality for an EMinQ.

The quality of a probabilistic result is an important issue. It enables us to determine if the uncertainty of any sensor data needs to be reduced (e.g., request an immediate update from the sensor) in order to improve the quality of result. In this section, we study two key factors that affect quality – size of uncertain intervals and entropy of probabilistic results.

1.The size of an uncertain interval indicates the extent of error inherent to a data value. A larger uncertain interval can result in poorer answer quality, as illustrated in Figure 2. Another example is the evaluation of VSumQ over two uncertain data

items Ti and Tj. The resulting value (i.e., Ti.a + Tj.a) lies in the error range [li(t)+lj(t), ui(t)+uj(t)]. It is desirable to have smaller Ui(t) and Uj(t) in order to obtain a smaller error range, or higher answer quality.

2.Entropy of probabilistic results: Consider two

sets of answers to an EMinQ: {(T1,0.3),(T2,0.2), (T3,0.5)} and {(T1,0.8), (T2,0.2)}. How do we know

which answer is more informative? Here, entropy gives us a convenient metric for measuring uncertainty of probabilistic results. According to Shannon (1949), entropy is defined as follows:

Let X1,…,Xn be all possible messages, with respective probabilities p(X1),…, p(Xn) such that ∑in=1 p(Xi ) = 1. Then the entropy of a message X {X1,…,Xn} is defined

Intuitively, H(X) measures the amount of uncertainty associated with a random message X. The larger the value of H(X), the more amount of uncertainty is in X.

We can use the idea of entropy to quantify the quality of query answers. Consider the entity-based non-aggre- gate query class, where each object is evaluated independent of other queries. The quality of each answer tuple (Ti,pi) can be specified in terms of entropy. For example, in an ERQ, each object Ti has a probability pi of satisfying the query, and (1-pi) otherwise. The entropy

of (Ti,pi) is then equal to –(pi log2 pi+(1-pi)log2(1- pi)). The overall entropy of an ERQ result is then equal to the

average of entropy values over all tuples of (Ti,pi) where

pi≠0.

For entity-based aggregate queries, recall that a set

R of tuples (Ti,pi) are returned, with ∑in=1 pi = 1 . We can

thus use H(R) to measure the answer uncertainty to these queries. The quality of the answer is lower if H(R) is higher.

A continuous version of the entropy definition can be used for value-based queries, defined as

tinuous random variable X with probability density function p(x) defined in the interval [l,u].

For more details on answer quality metrics for different query classes and heuristics that improve query quality, readers are referred to Cheng et al. (2003).

FUTURE TRENDS

Our next work is to study the indexing of probabilistic uncertain data in order to provide efficient access mechanisms to uncertain data. We also plan to study the join operation of uncertain data. We will also examine the efficient execution of a probabilistic threshold query, which is a probabilistic query with threshold λ—only

objects with probability value greater than λ are included in the answer. A preliminary study by Cheng & Prabhakar (2003) reveals that this variant of probabilistic queries is worth further study because it can improve the efficiency of probabilistic query algorithms significantly, by exploiting the fact that only objects with probability values higher than λ are returned.

Olston, C., Loo, B.T., & Widom, J. (2001). Adaptive precision setting for cached approximate values. Proceed- 5 ings of the ACM SIGMOD International Conference on Management of Data.

Olston, C., & Widom, J. (2000). Offering a precisionperformance tradeoff for aggregation queries over replicated data. Proceedings of the 26th International Conference on Very Large Data Bases.

CONCLUSION

In this article, we studied how uncertainty information can be incorporated to data values. Under the probabilistic uncertainty model, we discussed probabilistic queries where confidence in the result is expressed in terms of probability values. Probabilistic queries can be classified into two dimensions, according to the nature of a query answer, as well as whether aggregation operations are involved. Each query class requires a different evaluation algorithm, as well as an answer quality metric. We also discuss how the sizes of uncertain intervals and entropy of the answer affect the quality of a probabilistic result.

REFERENCES

Acharya, S., Gibbons, P., Poosala, V., & Ramaswamy, S. (1999). Join synopses for approximate query answering. Proceedings of the ACM SIGMOD International Conference on Management of Data.

Chatfield, C. (1989). The analysis of time series an introduction. Chapman and Hall.

Cheng, R., Kalashnikov, D., & Prabhakar, S. (2003). Evaluating probabilistic queries over imprecise data. Proceedings of the ACM SIGMOD International Conference on Management of Data, June.

Cheng, R., Kalashnikov, D., & Prabhakar, S. (2004). Querying imprecise data in moving object environments.

IEEE Transactions on Knowledge and Data Engineering, (to appear).

Cheng, R., & Prabhakar, S. (2003, December). Managing uncertainty in sensor databases. SIGMOD Record Issue on Sensor Technology.

Gibbons, P., & Matias, Y. (1998). New sampling-based summary statistics for improving approximate query answers. Proceedings of the ACM SIGMOD International Conference on Management of Data.

Olston, C., & Widom, J. (2002). Best-effort cache synchronization with source cooperation. Proceedings of the ACM SIGMOD International Conference on Management of Data (pp. 73-84).

Poosala, V., & Ganti, V. (1999). Fast approximate query answering using precomputed statistics. Proceedings of the 15th International Conference on Data Engineering (pp. 252).

Shannon, C. (1949). The mathematical theory of communication. University of Illinois Press.

Vrbsky, S.V., & Liu, J.W.S. (1994). Producing approximate answers to setand single-valued queries. The Journal of Systems and Software, 27(3).

Wolfson, O., Sistla, P., Chamberlain, S., & Yesha, Y. (1999). Updating and querying databases that track mobile units. Distributed and Parallel Databases, 7(3).

KEY TERMS

Entity-Based Query: A probabilistic query that returns a set of objects.

Interval Uncertainty: A model of sensor uncertainty where each stored data value is represented by a closed interval, called uncertain interval.

Point Uncertainty: A model of sensor uncertainty where each stored data item is assumed to be a correct representation of the entity being represented.

Probabilistic Query: A query which assumes data are characterized by probabilistic uncertainty, and returns query answers augmented with probability values.

Probabilistic Threshold Query: A probabilistic query with probability threshold », where only objects with probability values greater than » are included in the answer.

Probabilistic Uncertainty: A model of sensor uncertainty, where each data value is represented by its uncer-

tain interval, together with a probabilistic density function (called uncertain pdf) that describes the distribution of the values within the interval.

Sensor Uncertainty: An inherent property of a sen- sor-based application, where each recorded data item in the database is only an older, approximate version of the entity being monitored in the external environment.

Value-Based Query: A probabilistic query that returns a single value.

Sensors, Uncertainty Models, and Probabilistic Queries

ENDNOTE

1We only consider “atomic” queries that perform a single operation (e.g., range query). Complex queries that involve two or more operators (e.g., a SUM operation over a range query) are not covered by this classification scheme.

YanpuZhang

University of Nebraska at Omaha, USA

Zhengxin Chen

University of Nebraska at Omaha, USA

INTRODUCTION

Among the challenges of multimedia and mobile computing, providing a mechanism for data retrieval in multimedia databases under wireless mobile environments is one of the most difficult issues (Shih, 2001). Up to now, the fundamental technologies that are specialized for wireless mobile, multimedia environments are not mature in object-oriented, object-relational, as well as relational databases (Hillborg, 2002; Ramakrishnan & Gehrke, 2003; Watson, 2004). An important issue is how to ensure quick query response for the users. If a user found out that the retrieved multimedia object is neither interesting nor useful after it is displayed, then the time and bandwidth used for transmitting the multimedia objects have already been wasted. In order to save precious time and expensive bandwidth, it could be a good idea to let users browse objects at an acceptable resolution without paying much attention to the details or at the limited device display capability. This article presents a novel concept to deal with this problem by making use the concept of quality of service (QoS) to achieve adaptive query processing. In general, traditional QoS management is defined as the necessary supervision and control to ensure that the desired quality of service properties are attained and sustained, which applies both to continuous media interactions and to discrete interactions (Chalmers & Sloman, 1999). QoS thus consists of a set of specific requirements for

a particular service provided by a network to users. However, little work has been done in extending QoS principles to multimedia data management in wireless network environments.

MOTIVATION

Since a traditional DBMS does not support QoS-based objects (Shih, 2002), it only concentrates on tables that contain a large number of tuples, each of which is of relatively small size. However, a multimedia database management system (MM-DBMS) should support QoSsensitive multimedia data types in addition to providing all the facilities for DBMS functions. Once multimedia objects such as images, sound clips, and videos are stored in a database, individual objects of very large size have to be handled efficiently (Chang, Hung, & Shih, 2002). Furthermore, the crucial point is that mobile MM-DBMSs should have the QoS-based capabilities to efficiently and effectively process the multimedia data in wireless mobile environments.

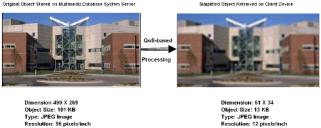
Figure 1 depicts a scenario where a client degrades his quality criteria and obtains a coarse query result with his limited display capacity within the acceptable response time. Suppose the client with a currently available PDA device queries a University of Nebraska Peter Kiewit Institute (PKI) image in a multimedia database through wireless networks. The client uses a GPRS